1, 2, …, n , …, то есть x_n = n ;     (1)

, то есть ;     (2)

,

то есть

;     (3)

,

то есть

;     (4)

  Если элементы числовой П. при достаточно больших номерах n сколь угодно мало отличаются от числа а, то П. называется сходящейся, а число а — еёпределом (аналогично определяется предел при функциональных П.). Например, П. (2) и (4) — сходящиеся, и их пределами служат число 0 и функция 1/(1 + x² ). Несходящиеся П., например (1) и (3), называются расходящимися.

Последовательные реакции

После'довательные реа'кции , химические процессы, в которых продукт одной реакции является исходным веществом др. реакции. К П. р. относятся такие важные химические процессы, как полимеризация , термический крекинг   углеводородов, хлорирование углеводородов и т.д. Так, при крекинге происходят последовательное превращение высокомолекулярных соединений во всё более низкомолекулярные и в то же время последовательные процессы образования высокомолекулярных соединений, бедных водородом (например, кокс). При хлорировании метана последовательно образуются CH₃ Cl, CH₂ Cl₂ , CHCl₃ и CCl₄ . Пример простой П. р. — последовательное протекание двух необратимых реакций первого порядка: А ® В ® С, где A, В, С — некоторые вещества. Изменение концентраций веществ во времени можно получить, интегрируя систему двух кинетических уравнений. Расчёт показывает, что концентрация промежуточного вещества В сначала растет, достигает некоторого максимального значения, а затем убывает.

  Более сложное описание П. р. получается в тех случаях, когда учитываются обратимость отдельных реакций, участие в них различных исходных веществ и т.п.

  Лит.: Эмануэль Н. М., Кнорре Д. Г., Курс химической кинетики, М., 1962; Родигин Н. М., Родигина Э. Н., Последовательные химические реакции. Математический анализ и расчёт, М., 1960; Бенсон С., Основы химической кинетики, пер. с англ., М., 1964.

Последовательный анализ

После'довательный ана'лиз в математической статистике, способ статистической проверки гипотез , при котором необходимое число наблюдений не фиксируется заранее, а определяется в процессе самой проверки. Во многих случаях для получения столь же обоснованных выводов применение надлежащим образом подобранного способа П. а. позволяет ограничиться значительно меньшим числом наблюдений (в среднем, т.к. число наблюдений при П. а. есть величина случайная), чем при способах, в которых число наблюдений фиксировано заранее.

  Пусть, например, задача состоит в выборе между гипотезами H₁ и H₂ по результатам независимых наблюдений. Гипотеза H₁ заключается в том, что случайная величина Х имеет распределение вероятностей с плотностью f₁ (x), a H₂ — в том, что Х имеет плотность f₂ (x ). Для решения этой задачи поступают следующим образом. Выбирают два числа А и В (0 < A < B ). После первого наблюдения вычисляют отношение l₁ = f₂ (x₁ )/f₁ (x₁ ), где x₁ — результат первого наблюдения. Если l₁ < A, принимают гипотезу H₁ ; если l₁ > B, принимают H₂ , если A £ l₁ £ B , производят второе наблюдение и так же исследуют величину l₂ = f₂ (x₁ ) f₂ (x₂ )/f₁ (x₁ ) f₁ (x₂ ), где x₂ — результат второго наблюдения, и т.д. С вероятностью, равной единице, процесс оканчивается либо выбором H₁ , либо выбором H₂ . Величины А и В определяются из условия, чтобы вероятности ошибок первого и второго рода (т. е. вероятность отвергнуть гипотезу H₁ , когда она верна, и вероятность принять H₁ , когда верна H₂ ) имели заданные значения a₁ и a₂ . Для практических целей вместо величины l_n удобнее рассматривать их логарифмы. Пусть, например, гипотеза H₁ состоит в том, что Х имеет нормальное распределение

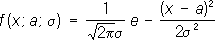
с a = 0, s = 1, гипотеза H₂ — в том, что X имеет нормальное распределение с a = 0,6, s = 1, и пусть a₁ = 0,01, a₂ = 0,03. Соответствующие подсчёты показывают, что в этом случае

и logl_n = 0.6

  Поэтому неравенства

 и  равносильны неравенствам

< 0.3n - 5.83

> 0.3n + 7.62

соответственно. Процесс П. а. допускает при этом простое графическое изображение (см. рис. ). На плоскости (хОу ) наносятся две прямые y = 0.3x - 5.83 и y = 0.3x + 7.62 и ломаная линия с вершинами в точках (n ,

), n = 1, 2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается H₂ , если через нижнюю, — H₁ . В приведённом примере для различения H₁ и H₂ методом П. а. требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез H₁ и H₂ по выборкам фиксированного объёма потребовалось бы более 49 наблюдений.

  Лит.: Блекуэлл Д., Гиршик М. А., Теория игр и статистических решений, пер. с англ., М., 1958: Вальд А., Последовательный анализ, пер. с англ., М., 1960; Ширяев А. Н., Статистический последовательный анализ, М., 1969.

  Ю. В. Прохоров.

Графическое изображение процесса последовательного анализа.

Последовательных приближении метод

После'довательных приближе'нии ме'тод, метод решения математических задач при помощи такой последовательности приближении, которая сходится к решению и строится рекуррентно (т. е. каждое новое приближение вычисляют, исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно). П. п. м. применяется для приближённого нахождения корней алгебраических и трансцендентных уравнений, для доказательства существования решения и приближённого нахождения решений дифференциальных, интегральных и интегро-дифференциальных уравнений, для качественной характеристики решения и в ряде др. математических задач. 1) Для решения уравнения