Если фазовое соотношение между компонентами (проекциями) Е меняется за времена, много меньшие времени измерения П. с., нельзя говорить о полной П. с. Однако может случиться, что в составляющих пучок света монохроматических волнах Е меняется не совершенно хаотически, а между взаимно перпендикулярными компонентами Е существует некоторый преимущественный фазовый сдвиг (фазовая корреляция), сохраняющийся в течение достаточно длительного времени. Физически это означает, что в поле световой волны амплитуда проекции Е на одно из взаимно перпендикулярных направлений всегда больше, чем на другое. Степень подобной фазовой корреляции в таком — частично поляризованном — свете описывают параметром р — степенью П. с. Так, если преимущественный фазовый сдвиг равен 0, свет частично линейно поляризован; ± p/2 — частично поляризован по кругу. Частично поляризованный свет можно рассматривать как «смесь» двух крайних видов — полностью поляризованного и естественного. Их соотношение и характеризуют параметром р, который часто (но не всегда) определяют как

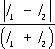
, где индексы 1 и 2 относятся к интенсивностям I света двух «ортогональных» поляризаций, например линейных во взаимно перпендикулярных плоскостях или соответствующих правой и левой круговым поляризациям; р может меняться от 0 до 100%, отражая все количественные градации состояния П. с. (Следует иметь в виду, что свет, проявляющийся в одних опытах как неполяризованный, в других может оказаться полностью поляризованным — с П. с., меняющейся во времени, по сечению пучка или по спектру.)

  В квантовой оптике электромагнитное излучение рассматривают как поток фотонов (см. Излучение , Квантовая механика , Оптика ). Состояния П. с. с квантовой точки зрения определяются тем, каким моментом количества движения обладают фотоны в потоке. Так, фотоны с круговой поляризацией (правой или левой) обладают моментом, равным ±

( — Планка постоянная ). Любое состояние П. с. может быть выражено всего через два т. н. базисных состояния. При описании П. с. выбор пары исходных базисных состояний неоднозначен — ими могут служить, например, любые две взаимно-ортогональные линейные П. с., правая и левая круговые П. с. и т.д., причём в каждом случае от одной пары базисных состояний можно по определённым правилам перейти к др. паре.

  Эта неоднозначность имеет в квантовом подходе принципиальный характер, однако «произвол» обычно ограничивают конкретные физические условия: наиболее удобно выбирать за базисную пару такие состояния П. с., которые преобладают в актах испускания фотонов элементарными излучателями либо определяют рассматриваемый процесс взаимодействия света и вещества. (Определение состояния П. с. на опыте осуществляется с помощью такого взаимодействия; по общим правилам квантовой механики подобный эксперимент всегда меняет — иногда пренебрежимо мало, иногда существенно — исходную П. с.) Базисные состояния и состояния, описываемые любой линейной комбинацией базисных (суперпозицией, см. Суперпозиции принцип ), называются чистыми. Они соответствуют полной П. с., со степенью П. с. 100%. Фотоны могут находиться не только в чистых, но и в т. н. смешанных состояниях, в которых степень их поляризации меньше 100% и может доходить до нуля (естественный свет). Смешанные состояния также выражаются через базисные, но более сложным образом, чем линейная суперпозиция (их называют некогерентной смесью чистых состояний). Взаимодействие света и вещества может в определённых условиях приводить к полному или частичному «выделению» чистых состояний из смешанных (за счёт упомянутого выше изменения П. с. при таком взаимодействии).

  Это явление используется для получения полностью поляризованного света или увеличения степени П. с. во многих поляризационных приборах . Если за базисные состояния П. с. выбраны две круговые (правая и левая) П. с., то при их наложении (когерентной суперпозиции) в равных долях наблюдается линейная П. с.; суперпозиции их в различных др. соотношениях дают эллиптические П. с. со всевозможными характеристиками. Через эти же базисные состояния могут быть выражены любые смешанные состояния. Т. о., тот или иной выбор всего двух базисных состояний даёт возможность описать все состояния П. с.

  Эксперименты подтверждают теоретический вывод о том, что каждый фотон, поляризованный по кругу, обладает моментом количества движения

= h /2p (см. Оптическая ориентация , Садовского эффект ). Характер поляризации фотонов определяется законом сохранения момента количества движения системы элементарный излучатель — испущенный фотон (при условии, что взаимодействием отдельных излучателей между собой можно пренебречь).

  Кроме особенностей элементарных актов излучения, к частичной (а иногда и полной) П. с. приводит множество физических процессов. К ним относятся, например, отражение света и преломление света , при которых П. с. обусловлена различием оптических характеристик границы раздела двух сред для компонент светового пучка, поляризованных параллельно и перпендикулярно плоскости падения (см. Брюстера закон ). Свет может поляризоваться при прохождении через среды, обладающие естественной или вызванной внешними воздействиями (индуцированной) оптической анизотропией (вследствие неодинаковости коэффициентов поглощения света при различных состояниях П. с., например при правой и левой круговых П. с. — т. н. круговой дихроизм, являющийся частным случаем плеохроизма ; вследствие различия преломления показателей среды для лучей различных линейных поляризаций — двойного лучепреломления , см. также Кристаллооптика ). Очень часто полностью поляризовано излучение лазеров ; одной из основных (но не единственной!) причин П. с. в лазерах является специфический характер вынужденного излучения , при котором поляризации испускаемого фотона и фотона, вызвавшего акт испускания, абсолютно тождественны; т. о. при лавинообразном умножении числа испускаемых фотонов в лазерном импульсе их поляризации могут быть совершенно одинаковыми. П. с. возникает при резонансном излучении в парах, жидкостях и твёрдых телах. П. с. при рассеянии света столь характерна, что её исследование — один из основных способов изучения как особенностей и условий самого рассеяния, так и свойств рассеивающих центров, в частности их структуры и взаимодействия между собой (см., например, Атмосферная оптика , Комбинационное рассеяние света ,Поляризация небесного свода ). (При рассеянии поляризованного света происходит и его деполяризация — уменьшение степени П. с.) В определённых условиях сильно поляризовано люминесцентное свечение (см. Люминесценция ), особенно при возбуждении его поляризованным светом. П. с. весьма чувствительна к величине напряжённости и ориентации электрических и магнитных полей; в сильных полях компоненты, на которые расщепляются спектральные линии испускания, поглощения и люминесценции газообразных и конденсированных систем , оказываются поляризованными (см. Зеемана эффект . Магнитооптика , Штарка эффект ).

  Одним из эффектов интерференции поляризованных лучей света является хроматическая П. с.

  Характерная для всех интерференционных явлений зависимость от длины волны («цвета») излучения приводит при этой «П. с.» (как показывает само название) к окрашиванию интерференционной картины, если исходный поток был белым светом . Обычная схема получения картины хроматической П. с. в параллельных лучах приведена на рис. 3 . В зависимости от разности хода обыкновенного и необыкновенного лучей, приобретаемой в двулучепреломляющей пластинке, наблюдатель видит эту пластинку (в свете, выходящем из анализатора) тёмной или светлой в монохроматическом свете либо окрашенной — в белом. Если пластинка неоднородна по толщине или по показателю преломления, её участки, в которых эти параметры одинаковы, видны соответственно одинаково тёмными или светлыми либо одинаково окрашенными. Линии одинаковой цветности называют изохромами. Схема для наблюдения хроматической П. с. в сходящихся лучах показана на рис. 4 , а получаемые при этом картины — на рис. 5 .