²

/27

],

(22)

Заметим, что здесь нам нужно учитывать члены порядка α₄² имея в виду взаимосвязь между деформациями вида 𝑃₂ и 𝑃₄ при конечных амплитудах. Находя минимум потенциальной энергии по переменной α₄, получаем

α

₄

=

-

243

595

α

₂

²

(23)

Это соответствует тому, что по мере того, как форма критической конфигурации становится всё более вытянутой с убыванием 𝑍²/𝐴, она приобретает вогнутость в области экваториального пояса, которая с уменьшением заряда ядра приводит непрерывным образом к той гантелевидной фигуре, которая обсуждалась в предыдущем пункте.

С помощью формулы (23) мы получаем энергию деформации как функцию одного параметра α₂. Непосредственным вычислением можно найти её максимальное значение, достигаемое с изменением α₂. Это даёт значение энергии, необходимой для создания такой деформации, когда ядро находится на грани деления,

𝐸_𝑓

4π𝑟₀²𝑂𝐴^2/3

=

𝑓(𝑥)

=

98

135

(1-𝑥)

³

-

11368

34425

(1-𝑥)

⁴

+….

(24)

Это выражение справедливо для значений 𝑍²/𝐴, близких к пределу стабильности.

Интерполируя разумным образом в интервале между двумя полученными предельными значениями критической энергии деления, получаем кривую (рис. 4) для 𝑓 как функции отношения квадрата заряда ядра к его массовому числу. В верхней части рисунка показан в увеличенном виде наиболее интересный участок кривой. Указанный справа масштаб энергии основан на оценке энергии поверхностного натяжения, даваемой формулой (12) при массе ядра 𝐴 = 235. Небольшим отличием множителя 4π𝑟₀²𝑂𝐴^2/3 для различных изотопов урана и тория можно пренебречь по сравнению с изменением множителя 𝑓(𝑥).

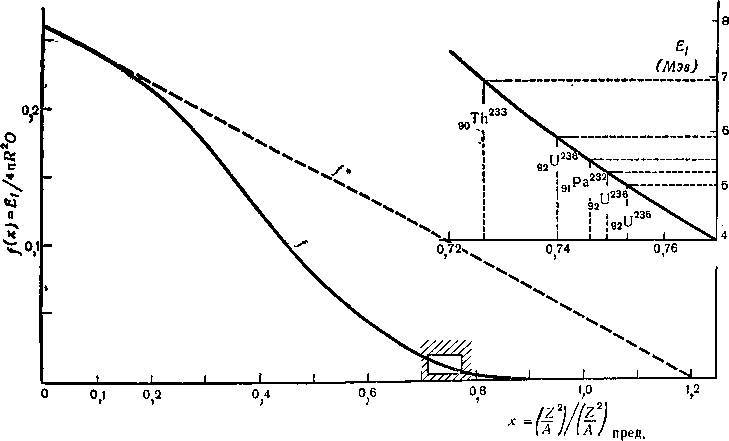
Рис. 4. Энергия 𝐸_𝑓 необходимая для создания критической деформации, приводящей к делению, поделена на энергию поверхностного натяжения 4π𝑅²⋅𝑂, чтобы получилась безразмерная функция величины 𝑥=(заряд)²[10 × (объём) × (коэффициент поверхностного натяжения)]. В тексте вычислено поведение функции 𝑓(𝑥) вблизи точек 𝑥=0 и 𝑥=1, после чего проведена плавная кривая, соединяющая две области этих значений. Приводимая для сравнения прямая 𝑓*(𝑥) определяет энергию, необходимую для такой деформации, когда ядро переходит в две соприкасающиеся сферы. В отмеченной штриховкой области, представляющей интерес для рассмотрения самых тяжёлых ядер, энергия поверхностного натяжения меняется незначительно. Принимая для неё значение 530 Мэв, получаем масштаб энергии в верхней части рисунка. В разделе IV мы находим из данных наблюдений оценку 𝐸_𝑓∼6 Мэв для U²³⁹. Отсюда с помощью рисунка можно найти (𝑍/𝐴)_{предельн.}=47,8 и оценить барьеры деления для других ядер, как указано на рисунке

В разделе IV мы на основании данных наблюдений получим оценку критической энергии деления для ядра U²³⁹, которая оказывается близкой к 6 Мэв. Согласно рис. 4, это соответствует значению 𝑥=0,74, откуда мы заключаем, что (𝑍/𝐴)_{предельн.} = 92²/(239⋅0,74)=47,8. Этот результат позволяет нам оценить критические энергии для других изотопов, как это показано на рисунке. Видно, что протактиний был бы особенно интересен как объект для экспериментов по изучению деления ядер.

Одним из побочных результатов нашего рассмотрения является возможность вычислить с помощью формулы (11) радиус ядра по известной величине энергии поверхностного натяжения. Принимая для 4π𝑟₀²𝑂 значение 14 Мэв, данное Финбергом, получаем 𝑟₀ = 1,47⋅10^-13 см, что удовлетворительно согласуется с результатом Финберга, определявшего радиус ядра по кривой коэффициента упаковки, и вместе с тем представляет совершенно независимую проверку этого результата.

До сих пор всё рассмотрение было чисто классическим. Однако в действительности всякое состояние движения, разумеется, должно описываться на языке квантовомеханических понятий. Использование классической картины в какой-то степени оправдывается малостью амплитуды нулевых колебаний обсуждавшегося выше типа по сравнению с радиусом ядра. Простой расчёт даёт следующий результат для квадрата отношения этих величин:

╱

╲

α

_𝑛

²

╲

╱ср. по осн. сост.

=

𝐴

^-7/6

×

×

⎡

⎢

⎣

ℏ²

12𝑀_𝑝 𝑟₀²

⋅

1

4π𝑟₀²𝑂

⎤1/2

⎥

⎦

𝑛

^1/2

(2𝑛+1)

^1/2

×

×

[

(𝑛-1)

(𝑛+1)

(2𝑛+1)

-

20(𝑛-1)𝑥

]

^-1/2

.

(25)

Поскольку

⎡

⎢

⎣

ℏ²

12𝑀_𝑝 𝑟₀²

⋅

1

4π𝑟₀²𝑂

⎤1/2

⎥

⎦

≈

1

3

,

это отношение действительно является малой величиной, и, следовательно, деформации, величина которых сравнима с размерами ядра, можно приближённо описывать классически посредством волновых пакетов, построенных из квантовых состояний. В частности, можно приближённо описывать классически критическую деформацию, приводящую к делению. Это следует из сравнения критической энергии 𝐸_𝑓 ∼ 6 Мэв, требуемой, как мы увидим в разделе IV, для объяснения данных наблюдений в случае урана, с энергией нулевых колебаний простейшего вида (капиллярные колебания), равной

1

2

ℏω

₂

=

𝐴

^-1/2

⎡

⎢

⎣

4π𝑟

₀

²

𝑂

⋅

2(1-𝑥)

×

×

ℏ²

3𝑀_𝑝 𝑟₀²

⎤1/2

⎥

⎦

≈

0,4

Мэв

.

(26)

Отсюда очевидно, что амплитуда рассматриваемой деформации значительно превосходит размер возмущений, создаваемых нулевыми колебаниями,

╱

╲ α₂²

╲

╱

ср.

╱

╲ α₂²

╲

╱

ср. по осн. сост.

∼

𝐸_𝑓

½ℏω₂

∼

15.

(27)

Капля, с которой мы сравниваем ядро, может совершать колебания около формы неустойчивого равновесия также и в критическом состоянии. Если рассмотреть распределение этих характеристических колебаний по частотам, то при больших частотах нам следует ожидать спектра, качественно не очень сильно отличающегося от спектра обычных колебаний нормальных видов около состояния устойчивого равновесия. Обсуждаемые колебания можно схематически представить на рис. 3 в виде движения изображающей точки системы в конфигурационном пространстве перпендикулярно направлению, которое ведёт к делению. Когда система находится вблизи критического состояния, распределение её энергии между такими видами движения и теми, которые ведут к делению, является определяющим для вероятности деления. Проблема нахождения её значения рассматривается с помощью статистической механики в разделе III. Здесь мы хотели бы лишь отметить, что процесс деления с практической точки зрения является почти необратимым процессом. Действительно, представим себе, что два ядра-осколка, возникшие в результате деления, отразились без потери энергии и стали двигаться прямо навстречу друг другу. Тогда в обычных условиях электростатическое отталкивание не позволит им прийти в соприкосновение. Это видно из рассмотрения разницы в энергии между начальным ядром и двумя сферическими ядрами вдвое меньшего объёма, которая даётся формулой (19) и связана с величиной 𝑓*(𝑥) изображённой на графике (см. рис. 4), пунктирной линией. Чтобы сравнить эту разницу с энергией, необходимой для первоначального процесса деления [сплошная кривая 𝑓(𝑥) на том же рисунке], заметим, что энергия поверхностного натяжения 4π𝑟₀²𝑂𝐴^2/3 для самых тяжёлых ядер порядка 500 Мэв. Отсюда получаем значение 0,05⋅500 Мэв = 25 Мэв для разности между энергией, которой обладает тяжёлое ядро при наступлении возможности деления, и той энергией, которая необходима для приведения в соприкосновение двух сферических осколков. Разумеется, при сближении осколков в них будут возникать вполне заметные приливные силы, но простая оценка показывает, что они снижают упомянутую разность энергий на величину около 10 Мэв, что не меняет наших выводов. Однако здесь нет парадокса; это следует из того факта, что процесс деления в действительности происходит через такую конфигурацию, в которой сумма энергии поверхностного натяжения и электростатической энергии значительно меньше, чем для двух соприкасающихся сфер, даже с учётом искажения формы за счёт приливных сил. Можно считать, что в ходе процесса деления разрыв поверхности, окружающей начальное ядро, происходит лишь тогда, когда энергия взаимного электростатического отталкивания двух возникающих ядер падает до значения, значительно меньшего, чем то, которое соответствует двум разделённым сферам. При этом запас электростатической энергии должен быть достаточным для совершения работы, которую нужно затратить для разрыва поверхности. Площадь же последней возрастает при этом до значения, большего, чем то, которое соответствует двум сферам. Отсюда ясно, что два образующихся при делении осколка будут обладать внутренней энергией возбуждения. Следовательно, если мы хотим обратить процесс деления, то мы должны сделать так, чтобы осколки сходились вновь достаточно деформированными, причём их деформации должны иметь такое направление, чтобы выступы их поверхностей могли прийти в соприкосновение и силы поверхностного натяжения начали стягивать их вместе, пока электростатическое отталкивание между эффективными центрами тяжести электрических зарядов двух частей ещё не стало слишком большим. Вероятность того, чтобы два атомных ядра в произвольном реальном столкновении оказались нужным образом возбуждёнными и обладали бы такими фазовыми соотношениями, чтобы было возможно их слияние с образованием составного ядра, должна быть крайне малой. Такие процессы слияния, обратные делению, могут ожидаться для невозбуждённых ядер лишь при кинетической энергии, гораздо большей, чем выделяющаяся в обсуждаемых здесь процессах деления.