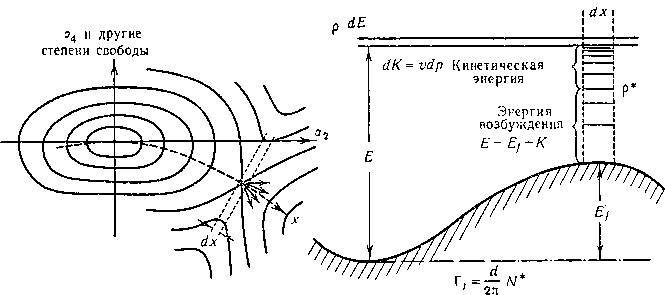
Рис. 3. Потенциальная энергия, связанная с произвольным изменением формы ядра, в зависимости от параметров, определяющих деформацию, может быть графически представлена некоторой поверхностью, горизонтали которой схематически изображены в левой части рисунка. Перевал, или седловидная точка, соответствует критической деформации неустойчивого равновесия. В той мере, в какой мы можем пользоваться классической картиной, течение реакции деления можно уподобить поведению шарика, лежащего в углублении в начале координат (сферическая форма ядра) и внезапно испытывающего толчок, который заставляет его колебаться около положения равновесия, описывая сложную фигуру Лиссажу. Если энергия достаточно велика, шарик с течением времени может случайно получить скорость в нужном направлении и преодолеть седловидную точку (это соответствует тому, что произошло деление) при условии, что он не потеряет до этого своей энергии (это соответствует испусканию нейтрона или гамма-кванта). Справа для иллюстрации расчёта вероятности деления в единицу времени, который делается в тексте, изображено сечение поверхности вдоль линии, пересекающей барьер деления
Простые соображения размерности показывают, что критическая энергия деформации для капли, соответствующей ядру с данным зарядом и массовым числом, может быть записана как произведение энергии поверхностного натяжения на безразмерную функцию отношения заряда к массе
𝐸
𝑓
=
4π𝑟
0
2
𝑂𝐴
⋅
𝑓
⎛
⎜
⎝
𝑍2/𝐴
(𝑍2/𝐴)предельн.
⎞
⎟
⎠
.
(13)
Мы можем определить 𝐸𝑓, если нам известна форма ядра в критическом состоянии. Последняя даётся решением известного уравнения для формы поверхности, находящейся в состоянии равновесия под действием силы поверхностного натяжения (определяемой коэффициентом поверхностного натяжения 𝑂) и объёмных сил, описываемых потенциалом φ:
𝑘𝑂+φ
=
const,
(14)
где 𝑘 — полная нормальная кривизна поверхности. Однако ввиду значительных трудностей, связанных с описанием больших деформаций, мы можем рассчитать форму критической поверхности и значение безразмерной функции 𝑓 в (13) лишь при некоторых специальных значениях аргумента, а именно:
1. Если объёмный потенциал в (14) полностью обращается в нуль, мы видим из (14), что поверхность неустойчивого равновесия имеет постоянную кривизну. Фактически мы имеем дело с делением жидкости на две сферы. Таким образом, в случае отсутствия электростатических сил, способствующих делению, критическая энергия при делении на два одинаковых осколка будет точно равна полной работе, которую нужно затратить против сил поверхностного натяжения в процессе разделения, т. е.
𝐸
𝑓
=
2⋅
4π𝑟
0
2
𝑂
(𝐴/2)
2/3
-
4π𝑟
0
2
𝑂
𝐴
2/3
.
(15)
Отсюда следует, что
𝑓(0)
=
2
1/3
-1
=
0,260.
(16)
2. Если заряд капли отличен от нуля, но всё же очень мал, критическая форма поверхности мало отличается от двух соприкасающихся сфер. При этом будет существовать узкий перешеек из жидкости, соединяющий две части фигуры; радиус его 𝑟𝑛 должен быть таким, чтобы обеспечить равновесие. В первом приближении
2π𝑟
𝑛
𝑂
=
(𝑍𝑒/2)2
[2𝑟0(𝐴/2)1/3]2
,
(17)
или
𝑟𝑛
𝑟0𝐴1/3
=
0,66
𝑍2/𝐴
(𝑍2/𝐴)предельн.
(18)
Чтобы рассчитать критическую энергию в первом порядке по 𝑍2/𝐴, можно пренебречь влиянием перешейка, которое приводит к изменению энергии лишь во втором порядке. При этом нам достаточно сравнить сумму энергии поверхностного натяжения и электростатической энергии для первоначального ядра с соответствующей величиной для двух соприкасающихся сферических ядер вдвое меньшего объёма. Находим
𝐸
𝑓
=
2⋅
4π𝑟
0
2
𝑂
(𝐴/2)
2/3
-
4π𝑟
0
2
𝑂
𝐴
2/3
+
+
2⋅
3(𝑍𝑒/2)2
5𝑟0(𝐴/2)1/3
+
(𝑍𝑒/2)2
2𝑟0(𝐴/2)1/3
-
3(𝑍𝑒/2)2
5𝑟0𝐴1/3
(19)
откуда
𝐸𝑓
4π𝑟02𝑂𝐴2/3
≡
𝑓(𝑥)
=
0,260-0,215𝑥,
(20)
где
𝑥
=
𝑍2/𝐴
(𝑍2/𝐴)предельн.
=
=
(Заряд)2
(Коэффициент поверхностного
натяжения)×(Объём)×10
(21)
считается малой величиной.
3. В случае, представляющем наибольший практический интерес, когда 𝑍2/𝐴 очень близко к критическому значению, для достижения критического состояния достаточно лишь небольшого отклонения от сферической формы. Согласно равенству (9), потенциальная энергия, необходимая для бесконечно малого изменения формы, растет пропорционально квадрату амплитуды, причём наименьшее значение энергии соответствует деформации вида 𝑃2(cos θ). Чтобы найти деформацию, при которой потенциальная энергия достигает максимума и начинает убывать, мы должны провести более тщательные расчёты. С точностью до четвёртого порядка по α2 мы получаем для энергии деформации выражение
Δ𝐸
𝑆+𝐸
=
4π𝑟
0
2
𝑂𝐴
2/3
[
2α
2
2
/5
+
11α
2
3
/105
+
+
101α
2
4
/35
+
2α
2
2
α
4
/35
+
α
4
2
]-
-
3(𝑍𝑒/2)2
5𝑟0𝐴1/3
[
α
2
2
/5
+
64α
2
3
/105
+
58α
2
4
/35
+
+
8α
2
2
α
4
/35
+
5α
4