9 N. Bohr. Nature, 1936, 137, 344, 351 (статья 45); N. Bohr, F. Kalckаr. Kgl. Danske Vid. Selskab., Math.-Fys. Medd., 1937, 14, № 10 (статья 48).
10 После того как были получены приводимые ниже формулы, Финбергом (Phys. Rev., 1939, 55, 504) и Вейцзекером (Naturwiss., 1939, 27, 133) были опубликованы выражения для потенциальной энергии, связанной со сфероидальными деформациями ядер. Далее профессор Френкель из Ленинграда любезно прислал нам рукописный экземпляр более подробной статьи о различных аспектах проблемы деления, которая должна появиться в ЖЭТФ (ЖЭТФ, 1939, 9, 641. — Ред.). В ней содержится вывод уравнения (9) (см. ниже), описывающего стабильность ядра относительно произвольно малых деформаций, а также некоторые замечания о форме капли в состоянии неустойчивого равновесия, подобные сделанным ниже замечаниям [см. уравнение (14)]. Краткое резюме этой статьи появилось в «Physical Review» (Phys. Rev., 1939, 55, 987).
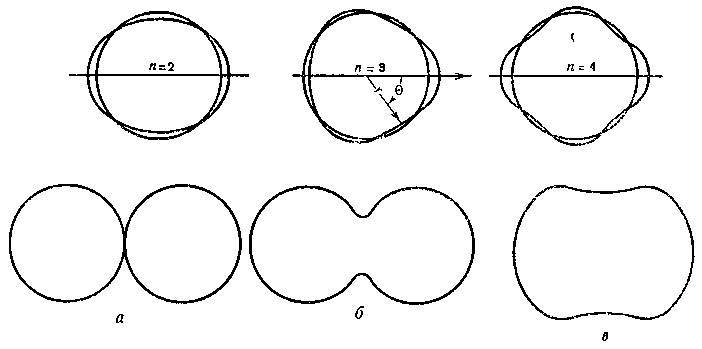
Рис. 2. Малые деформации жидкой капли, описываемые формулой δ𝑟(θ)=α𝑛𝑃𝑛(cos θ) (верхняя часть рисунка), приводят к характерным колебаниям около сферической формы устойчивого равновесия, даже если жидкость имеет некоторый равномерно распределённый электрический заряд. Однако по достижении зарядом критического значения, равного [ 10 × (коэффициент поверхностного натяжения) × (объём) ½], сферическая форма становится неустойчивой по отношению к бесконечно малым деформациям чётного типа (с 𝑛 = 2). С другой стороны, при несколько меньших значениях заряда требуется конечная деформация (в) для достижения конфигурации неустойчивого равновесия, и с уменьшением плотности заряда критическая форма постепенно переходит (в, б, а) в две незаряжённые сферы, разделённые бесконечно малым расстоянием (а)
Рассмотрим малую произвольную деформацию жидкой капли, с которой мы сравниваем ядро. Пусть расстояние от центра до некоторой точки на поверхности с полярным углом θ меняется от первоначальной величины 𝑅 до значения
𝑟(θ)
=
𝑅[1
+
α
0
+
α
2
𝑃
2
(cos θ)
+
α
3
𝑃
3
(cos θ)
+
…],
(8)
где α𝑛 — малые величины (рис. 2). Непосредственное вычисление показывает, что сумма энергии поверхностного натяжения и электростатической энергии возросла до величины
𝐸
𝑆+𝐸
=
4π(𝑟
0
𝐴
1/3
)
2
𝑂
[
1+
2α
2
2
/5
+
5α
3
2
/7
+
+
(𝑛-1)(𝑛+2)α
𝑛
2
/
2(2𝑛+1)
+…
]+
+
3(𝑍𝑒)
2
/5𝑟
0
𝐴
1/3
[
1-α
2
2
/5
-
10α
3
2
/49
-…
-
-5(𝑛-1)α
𝑛
2
/
(2𝑛+1)
2
-…],
(9)
Здесь принято, что капля образована несжимаемой равномерно заряженной жидкостью, так что объем её равен (4π/3)𝑅3 = (4π/3)𝑟03𝐴 и заряд 𝑍𝑒; коэффициент поверхностного натяжения жидкости обозначен через 𝑂. Рассматривая коэффициент при α22 в приведённом выражении для энергии деформации, а именно:
4π𝑟
0
2
𝑂𝐴
2/3
⋅
2
5
⎡
⎢
⎣
1-
𝑉2
𝐴
⋅
𝑒2
10⋅(4/3)⋅π𝑟03𝑂
⎤
⎥
⎦
,
(10)
легко заметить, что с увеличением отношения 𝑍2/𝐴 мы приближаемся к предельному значению
⎛
⎜
⎝
𝑍2
𝐴
⎞
⎟
⎠предельн.
=
10⋅4π𝑟03𝑂
3𝑒2
(11)
за которым ядро перестаёт быть стабильным по отношению к деформациям простейшего типа. Численные значения фигурирующих здесь множителей можно получить с помощью предложенной Бете полуэмпирической формулы, описывающей относительный вклад в энергию связи ядра электрических и короткодействующих сил, причём влияние последних разделяется на объёмный и поверхностный эффекты. Значения констант, входящих в формулу Бете, были уточнены Финбергом 11 с точки зрения наилучшего согласия с дефектами масс Демпстера. Финберг нашёл
𝑟
0
≈
1,4⋅10
-13
см
,
4π𝑟
0
3
𝑂
≈
14
Мэв
.
(12)
Из этих значений предел отношения 𝑍2/𝐴 получается на 17% большим, чем соответствующее отношение для ядра U238, равное (92)2/238. Отсюда можно сделать вывод, что ядра, подобные урану и торию, действительно лежат вблизи предела стабильности, обусловленного точной компенсацией действия электростатических и короткодействующих сил. С другой стороны, точное значение предела, даваемое этими полуэмпирическими и косвенными определениями отношения поверхностной энергии к электростатической, нельзя считать надёжным, и ниже мы обсудим метод получения рассматриваемого отношения путём изучения самого явления деления.
11 Е. Feenberg. Phys. Rev., 1939, 55, 504.
Ядра, для которых величина 𝑍2/𝐴 несколько меньше предельного значения (11), стабильны по отношению к малым произвольным деформациям; однако деформации большей величины приводят к тому, что отталкивание за счёт дальнодействующих сил начинает преобладать над притяжением, создаваемым короткодействующими силами, ответственными за поверхностное натяжение. Поэтому ядро, должным образом деформированное, оказывается в состоянии самопроизвольно делиться. Особенно важен случай критической деформации, когда ядро находится как раз на грани деления. При этом капля приобретает форму, соответствующую состоянию неустойчивого равновесия: работа, затрачиваемая на бесконечно малое отклонение от этой равновесной конфигурации, в первом порядке обращается в нуль. Чтобы изучить это состояние несколько подробнее, рассмотрим поверхность, которая получается, если откладывать на графике энергию произвольной деформации в зависимости от параметров, определяющих форму и величину этой деформации. При этом нужно иметь в виду, что потенциальный барьер, препятствующий делению, должен иметь седловидную точку, которую можно сравнить с перевалом, соединяющим две долины на этой поверхности. Энергетические соотношения схематически показаны на рис. 3; конечно, мы можем представить на рисунке лишь два из большого числа параметров, которые требуются для описания формы капли. Значения параметров деформации, соответствующие седловидной точке, дают критическую форму капли; потенциальную энергию 𝐸𝑓, требуемую для такой деформации, мы будем называть критической энергией деления. Рассмотрим непрерывное изменение формы капли, приводящее от первоначальной сферы к двум сферам вдвое меньшего объёма, удалённым друг от друга на бесконечное расстояние. При этом критическая энергия, которой мы интересуемся, есть наименьшее значение энергии, необходимой для перехода от начальной конфигурации к конечной, которое можно получить, выбирая различным образом последовательность промежуточных конфигураций.