Теперь мы можем вернуться к вопросу о близнецах с большим числом партнеров, чем пять.

По закону Эллина шестерни родятся чрезвычайно редко — примерно один раз на 4712 миллионов родов. Шестерни насчитываются единицами в литературе. Их, по-видимому, установлено около 6 ко времени окончания второй мировой войны (Gates, 1946). К ним присоединился еще один случай, тоже недостаточно достоверный (Newman, 1948). Ни одна шестерня не сохранилась полностью и не была изучена.

Семерни, если можно так выразиться, настолько редки, что о них в литературе почти нет сведений. В Германии (город Гамелн) описан памятник в виде барельефа, воздвигнутый по случаю смерти в 1600 г. семерни, состоявшей из двух мальчиков и пяти девочек и недолго жившей (рис. 132). Все семь младенцев изображены на памятнике (Cook, 1934, и др.). Случай якобы родившейся в 1907 г. семерни описал Томас (Thomas, 1921). По газетам, в Испании в 1943 г. будто бы был случай родов семи живых детей, из которых двое сразу умерли (Caullery, 1945).

Вероятность рождения семерни, а тем более восьмерни, вообще ставится под сомнение. До сих пор, по-видимому, нет еще ни одного случая, достоверно установленного, в печати же появлялись заведомо лживые сообщения такого рода. Примером может служить заметка в одном американском журнале в 1872 г. Об этом случае недавно писал Ньюмен (1948). Оказалось, что это сообщение будто бы злонамеренная фальшивка, написанная отвергнутым поклонником той дамы, которой приписывались столь многоплодные роды (Guttmacker, 1948).

Человеческие близнецы, особенно ОБ, изучены во многих отношениях гораздо глубже и разностороннее, чем близнецы животных. Это объясняется не только исключительным интересом к человеку, как объекту изучения взаимодействия факторов наследственности и среды, для чего служат исследования морфологии, физиологии и психологии близнецов в норме и патологии, но и тем удивительным фактом, что относительное количество ОБ у человека оказывается большим, чем у высших млекопитающих, как мы это видели из вышеизложенного материала. Это позволяет изучать не только отдельные «случаи» человеческих близнецов, т. е. единичные пары, как это приходится делать при изучении близнецов у коров, лошадей, обезьян и т. д., но для ряда признаков использовать десятки и даже сотни пар, что дает возможность статистически обрабатывать полученные данные (например, это делалось Коллманом при изучении туберкулеза и шизофрении, см. главу двенадцатую «Заболевания нервной системы»). В таких случаях изучение сходства и различия близнецов требует возможно большего материала. При этом необходимо соблюдать одно очень важное методическое правило, значение которого выяснилось только постепенно, ценой ряда ошибочных выводов. Собирая материал, нельзя ограничиваться только отдельными «интересными» случаями, соответствующими теоретическим предположениям исследователя и потому «нравящимися» ему. Сбор материала должен производиться без отбора в этом смысле, серия пар должна быть «безотборная», даже включать тех близнецов, один из партнеров которых умер (Allen, 1955b). Только в такой безотборной серии изучаемый признак может обнаружиться со свойственным ему многообразием проявления и в тех количественных отношениях, которые соответствуют реальной действительности и поэтому пригодны для суждения о роли наследственности в его проявлении. Так, например, интересуясь наследственностью рака, некоторые исследователи отбирали только те случаи ОБ, когда оба близнеца имели раковую опухоль. Сравнивая такую серию ОБ с серией РБ, где встречаются пары, имеющие только одного ракового больного, делали вывод, что среди ОБ больше конкордантных пар (т. е. внутрипарно похожих по данному признаку), чем среди РБ, а следовательно, ввиду одинаковой наследственности ОБ рак возникает на базе «наследственного предрасположения» к нему и т. д. Сравнение безотборной серии ОБ, т. е. серии, в которую включались все те пары близнецов, где хоть один партнер болел раком, с безотборной серией РБ показало всю ошибочность такого вывода, а вместе с тем и способа сбора материала, к нему приводящего (см. главу двенадцатую «Рак»). Одним из признаков такой безотборности сравнительно большого материала служит количественное отношение пар близнецов в серии ОБ и серии РБ: оно должно приближаться к отношению чисел этих двух типов близнецов в популяции, т. е. число пар РБ должно быть раза в 3—4 больше, чем число пар ОБ.

Ряд признаков на близнецах еще не изучен на больших безотборных сериях. Приходится обращаться к работам, сделанным на малом материале, иногда в той или иной степени отобранном, что, конечно, снижает значение статистической обработки такого материала и выводы из него. Это приходится помнить при рассмотрении соответствующих работ и видеть их относительную ценность.

Теперь, переходя к конкретному материалу, мы сначала обратимся к некоторым общим признакам, как например рост и вес, легко измеримым, а затем перейдем к рассмотрению отдельных частей тела и органов близнецов.

Признаки измеримые, выражающие размеры тела и соотношения частей его, не раз изучались на близнецах различных стран (Verschuer, 1927 — 1954; Бунак, 1926; Dahlberg, 1926; Stocks, 1930; Newman et al., 1937, и др.). В качестве примера такого рода материала рассмотрим таблицу Бунака (1926), составленную на основании обмера московских близнецов в возрасте 13—16 лет при условии, что каждая пара жила приблизительно в одинаковых условиях (табл. 11).

Мы видим, что величина М для РБ значительно больше, чем для ОБ, что говорит о большем внутрипарном сходстве ОБ.

Аналогичная картина получена для московских детей в возрасте 8—10 лет (Соболева и Игнатьев, 1936) с помощью другого приема — вычисления коэффициента корреляции между близнецами каждой пары (табл. 12). Как известно, чем больше коэффициент корреляции приближается к единице, тем больше сходство для этих признаков.

В ряде работ внутрипарная разница в общей форме вычисляется с помощью простого приема, предложенного Фершюром (Verschuer, 1927), так называемого процентного отклонения («Е»), Эта величина вдвое меньше, чем вычисленная Бунаком в табл. 11 («М»), так как Фершюр, как мы сейчас увидим из примера, берет половину внутрипарной разницы в процентах к средней величине пары близнецов, а Бунак —не половину разницы, а всю. Для получения процентного уклонения по Фершюру сначала вычисляется средняя величина двух каких-нибудь измерений данной пары близнецов, а затем отклонение от нее в процентах. Например, если один из близнецов имеет рост 168.4 см, а другой 170.2 см, то средняя величина роста обоих будет 169.3 см, а отклонение от нее каждого из близнецов будет равняться 0.9 см. Процентное уклонение данной пары от средней величины их роста будет равно 0.9x100 : 169.3 = 0.53%. Чтобы получить среднее процентное отклонение для нескольких пар близнецов, берется средняя величина процентных отклонений этих пар. Фершюр получил цифры такого среднего процентного отклонения для нескольких признаков обоих типов близнецов из немецкого населения (табл. 13).

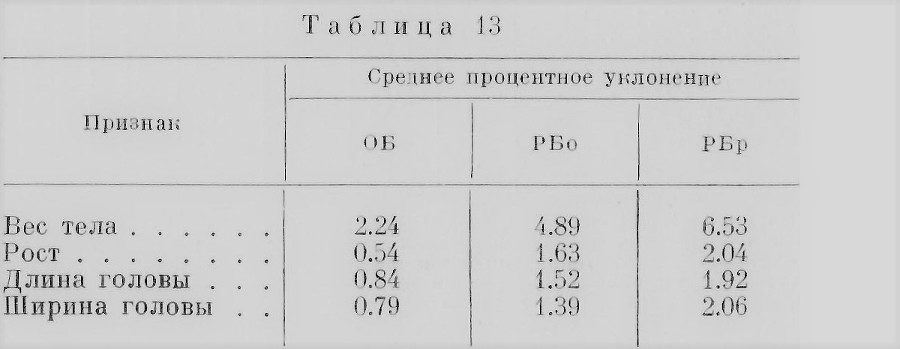
Эти цифры также показывают большее впутрипарное сходство ОБ по сравнению с РБ, а среди РБ — относительно большее сходство близнецов одинакового пола, чем разного.

Среди приведенных признаков одни оказываются более внутрипарно похожими, чем другие, например рост в среднем больше похож, чем вес, и это независимо от типа близнецов. Связь этих признаков с возрастом будет рассмотрена в другом месте (см. глава тринадцатая).

Внутрипарные различия обоих типов близнецов можно для разных признаков изобразить также графически, если, например, на абсциссе отложить числа, характеризующие эти различия, а на ординате — частоты в виде числа пар в процентах, как это сделал Ньюмен с сотрудниками (Newmen et al., 1937) для 50 пар ОБ и 50 пар РБ. В качестве примера мы приводим кривые для роста, длины головы и веса (рис. 133).