Дальнейшая процедура очевидна. Мы пытаемся определить константы, исходя их условия, что

(

𝑇

^μν

+

χ

^μν

)

_,ν

=

0.

(5.5.5)

Эти условия дают множество более, чем 18 уравнений для 18 констант. Тем не менее, оказывается, что все уравнения совместны и 18 констант определяются однозначно. Когда мы сделаем это, у нас будет уточнённая теория, которая правильно учитывает энергию самого гравитационного поля во втором порядке по ℎ_μν.

Лекция 6

6.1. Билинейные члены тензора энергии-импульса

Наша нынешняя теория линейна в том смысле, что мы написали уравнение относительно гравитационного поля ℎ_μν связывающего его с тензором давления 𝑇_μν

ℎ

_μν,λ

^,λ

-

2

ℎ

_μλ,ν

^,λ

=-

λ𝑇

_μν

.

(6.1.1)

Но мы определили 𝑇_μν, выразив его только через распределение материи, как будто на материю не действует гравитация, как будто энергия гравитационного поля сама по себе не является источником полей. Эффекты, связанные с влиянием гравитации на материю, которые мы хотели бы включить в рассмотрение, могут быть проиллюстрированы рассмотрением того, что может произойти, когда мы соединяем массы объектов 1 и 2 вместе в присутствии третьего объекта. Часть работы, которая произведена, может пойти на нагревание третьего объекта, так что энергия не сохраняется при рассмотрении только масс объектов 1 и 2 и полей, которые они порождают. Таким образом, энергия не сохранялась бы, если бы мы рассматривали только подсистемы; ящики, показанные штриховыми линиями на рис. 6.1, не имели бы одинаковый вес. Нелинейный эффект, обусловленный влиянием энергии поля, является более знакомым; мы вычислили поля, обусловленные распределением массы, как первое приближение; следующее приближение состоит в том, чтобы включить поля первого порядка как источники, и так мы приходим к самосогласованному решению.

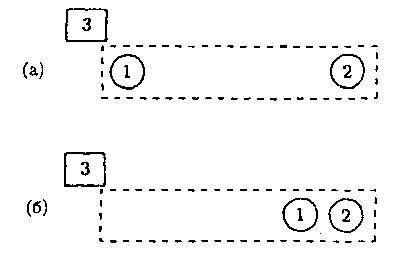
Рис. 6.1.

Мы построим новый тензор давления из нашего старого тензора добавлением члена, который будет выводим из той части лагранжиана, которой пренебрегали ранее, и который обозначим 𝐹³, путём вариации

^new

𝑇

^μν

=

^old

𝑇

^μν

+

χ

^μν

,

λχ

^μν

=

δ𝐹³[ℎ]

δℎ_μν

,

(6.1.2)

и надеемся, что эти трудности будут устранены, по крайней мере, в более высоких порядках по ℎ_μν

Так как мы пытаемся построить χ^μν для того, чтобы устрашить тот недостаток тензора энергии-импульса ^old𝑇^μν≡^o𝑇^μν, связанный с сохранением энергии ^o𝑇^μν_,ν≠0, мы получаем намёк на структуру χ^μν, вычисляя дивергенцию ^o𝑇^μν_,ν. Дивергенция χ^μν взаимно уничтожила бы ненулевую часть этой дивергенции ^o𝑇^μν_,ν, по крайней мере, в первом ненулевом порядке. Для того, чтобы вычислить эту дивергенцию, мы сначала перепишем тензор ^o𝑇^μν для движущейся частицы в новой форме, которая выглядит сначала непривычной, но с которой проще проводить преобразования. На языке интеграла по скалярному параметру, который также может быть собственным временем 𝑠 (мы обозначаем точками производные по собственному времени 𝑠), получаем следующее выражение для этого тензора

^o

𝑇

^μν

(𝑥)

=

𝑚₀

∫

𝑑𝑠δ⁴

(𝑥-𝑧(𝑠))

𝑧̇

^μ

𝑧̇

^ν

.

(6.1.3)

То, что это выражение для тензора ^o𝑇^μν эквивалентно тому, которое было использовано ранее, может быть проверено сравнением соответствующих членов действия

λ

∫

𝑑⁴𝑥

^o

𝑇

^μν

(𝑥)

ℎ

_μν

(𝑥)

=

λ

𝑚₀

∫

𝑑𝑠

ℎ

_μν

(𝑧)

𝑧̇

^μ

𝑧̇

^ν

.

(6.1.4)

Существует простой физический путь для интерпретации смысла δ-функции в соотношении (6.1.3); в этом выражении попросту утверждается то, что нет энергии взаимодействия, за исключением того места, где на самом деле находится частица. Возможно проще понять, насколько удачно подобраны эти выражения, переписывая обычную электродинамику на том же самом языке; член в лагранжиане, описывающий взаимодействие, есть объёмный интеграл от -𝑗^μ𝐴_μ а 𝑗^μ связывается со скоростью частицы следующим образом:

𝑗

^μ

(𝑥)

=

𝑒

∫

𝑑𝑠δ⁴

(𝑥-𝑧(𝑠))

𝑧̇

^μ

,

𝑆(внутр)

=-

𝑒

∫

𝑑𝑠

𝐴

_μ

(𝑧)

𝑧̇

^μ

.

(6.1.5)

Параллелизм с нашими гравитационно-полевыми выражениями (6.1.3) и (6.1.4) очевиден.

Вычислим дивергенцию ^o𝑇^μν_,ν из соотношения (6.1.3). Сначала проверим, что δ-функция симметрична по переменным 𝑥 и 𝑧, так что производная по переменной 𝑥^ν может быть заменена (со знаком "-") производной по переменной 𝑧^ν. Тогда мы будем использовать следующее тождество

𝑧̇

^ν

∂

∂𝑧^ν

ƒ[𝑧(𝑠)]

=

𝑑

𝑑𝑠

ƒ[𝑧(𝑠)]

(6.1.6)

для того, чтобы получить выражение для дивергенции тензора ^o𝑇^μν

^o

𝑇

^μν

_,ν

=

𝑚₀

∫

𝑑𝑠δ⁴

(𝑥-𝑧(𝑠))

𝑧̈

^μ

.

(6.1.7)

Мы видим, что эта дивергенция есть плотность ускорения. Здесь мы будем предполагать, что мы уже правильно включили в наш лагранжиан все взаимодействия, отличные от гравитации, так что ускорение 𝑧̈^μ представляет влияние гравитации, задаваемое уравнением движения

𝑔

_μλ

𝑧̈

^μ

=-

1

2

[

𝑔

_μλ,ν

+

𝑔

_νλ,μ

-

𝑔

_μν,λ

]

𝑧̇

^μ

𝑧̇

^ν

=-

[μν,λ]

_𝑧

𝑧̇

^μ

𝑧̇

^ν

.

(6.1.8)

Нижний индекс 𝑧 на скобке напоминает нам, к какой переменной относятся индексы. Теперь умножим дивергенцию, полученную в соотношении (6.1.7), на 𝑔_μλ(𝑥) и заменим 𝑔_μν𝑧̈^μ на -[μν,λ]_𝑧𝑧̇^μ𝑧̇^ν. Заметим, что из-за наличия δ-функции величина [μν,λ]_𝑧 приводит к тому же эффекту, что и [μν,λ]_𝑥. Это означает, что знак скобки может быть вынесен за знак интеграла, приводя нас к выражению, в которое включена только дивергенция ^o𝑇^μν_,ν и исходный тензор ^o𝑇^μν: