𝐺'³

𝑚₁

𝑚₂

𝑚₃

𝑖²

∫

𝑑𝑠 𝑑𝑡

(𝑠²-𝑟₁₂)(𝑡²-𝑟₂₃)[(𝑠-𝑡)²-𝑟₃₁]

.

(2.4.3)

Этот интеграл может быть вычислен последовательным интегрированием в каждом из полюсов и результат равен

𝐸

=-

𝐺'³

𝑚₁

𝑚₂

𝑚₃

π²

1

(𝑟₁₂-𝑟₂₃-𝑟₁₃)𝑟₁₂𝑟₂₃𝑟₁₃

.

(2.4.4)

Если одна из масс, скажем масса номер 3, существенно удалена, так что 𝑟₁₃ много больше, чем 𝑟₁₂, то мы, действительно, получаем, что взаимодействие между массами номер 1 и номер 2 обратно пропорционально величине 𝑟₁₂.

Что же такое масса 𝑚₃? Это, очевидно, может быть некоторая эффективная средняя величина по всем другим массам во вселенной. Влияние удалённых масс, сферически распределённых вокруг масс 1 и 2, проявилось бы как интеграл по средней плотности; мы бы имели

𝐸

=-

𝐺'³𝑚₁𝑚₂π²

𝑟₁₂

∫

4πρ(𝑅)𝑅²𝑑𝑅

2𝑅³

,

(2.4.5)

где 𝑅 - большое значение расстояния 𝑅≈𝑟₁₂≈𝑟₂₃ Для простой оценки мы можем взять плотность, равной константе внутри сферы; мы выполним интегрирование от некоторого начального значения радиуса, которое, тем не менее, достаточно большое по сравнению со значением 𝑟₁₂. Вклад всех масс вне сферы с этим минимальным значением радиуса является чем-то типа

𝐸

=-

𝑚₁𝑚₂

𝑟₁₂

2π³

𝐺'³

ln

⎛

⎜

⎝

𝑅₀

𝑅_𝑖

⎞

⎟

⎠

ρ

.

(2.4.6)

Этот логарифм является некоторой величиной, которая не может быть многим больше, чем 50 или 100, так как характерное значение внешнего радиуса может быть равно 𝑇𝑐=10¹⁰ световых лет 10²⁸ см. Такая энергия действует подобно гравитации; можем ли мы опровергнуть это? Да, и двумя способами. Во-первых, величина этого логарифмического члена становится сравнимой с величиной всей силы (2.4.2), пропорциональной 1/𝑟³, на расстояниях больших, чем те, на которых ньютоновский закон гравитации уже проверен. Более того, если мы рассматриваем влияние Солнца на гравитационное взаимодействие между Землёй и Луной, мы обнаруживаем, что это влияние должно было бы приводить к наблюдаемым отклонениям в орбитальном движении, так как расстояние от Земли до Солнца меняется при движении Земли вдоль своей орбиты. Мы оцениваем этот эффект следующим образом. Мы хотим сравнить вклад Солнца во взаимодействие Земля - Луна со вкладом всех остальных звёзд. Это влияние зависит от массы и обратно пропорционально кубу расстояния. Для логарифма меньшего, чем 1000, вклад Солнца превосходит в 10¹² вклад звёзд для любой разумной оценки плотности звёзд! Таким образом, мы можем пренебречь вкладом звёзд. Но таких больших возмущений, которые бы соответствовали изменению эффективной гравитационной константы, которое бы возникало от ±2 процентной вариации расстояния между Землёй и Солнцем, не наблюдалось в системе Земля - Луна.

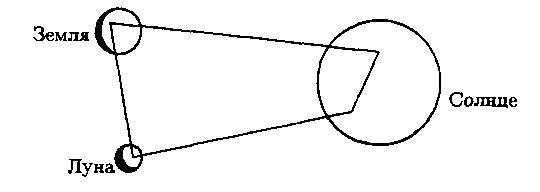
Рис. 2.6.

Но можно ли всё-таки спасти эту теорию? Представляется, что процессы более высокого порядка могли бы снять эти трудности, например процесс, включающий 4 нейтринных линии или даже более высокие порядки, мог бы быть вычислен. Ясно, что член, изображённый на рис. 2.6, мог бы дать вклад порядка 𝑚₃², т.е. квадрата числа частиц окружающих масс, и, следовательно, влияние удалённой туманности могло бы значительно превзойти влияние Солнца. Этот факт мог бы быть ещё более справедливым для более высоких порядков теории. Мы должны, следовательно, суммировать диаграммы различных порядков, типа изображённых на рис. 2.7.

Рис. 2.7.

Тем не менее, насколько я могу судить из статистики Ферми, члены различных порядков оказываются противоположными по знаку и никакого удовлетворительного результата не получается.

Чтобы объяснить эту идею более формально, мы полагаем, что в теории (где есть, скажем, скаляр ψ) с квадратичной связью ψφ²ψ математическое ожидание для произведения двух полевых переменных φ(1)φ(2) в состоянии при наличии многих туманностей может определяться соотношением

〈φ(1)φ(2)〉

=

δ

₊

(𝑆₁₂²)

+

𝐶

(2.4.7)

где первый член есть обычный вакуумный член, а 𝐶 возникает от взаимодействия с удалённой туманностью. Величина 𝐶 практически не зависит от 1 и 2, если они (1 и 2) близки по сравнению с радиусом вселенной.

Тем не менее, я думало, что для спина 1/2 не может возникать 𝐶. Для фотонов такой член, даже если он возникает, не имел бы желаемого эффекта, т.к. насколько я могу видеть, этот член не является квадратичным для связи фотонов.

Итак, теория с двойной нейтринной парой не привела к плодотворному результату. Однако, мы научились кое-чему, работая с этой теорией от начала до конца, что представляет собой весьма замечательную идею. Если мы построим теорию гравитации, основанную на взаимодействии трёх тел, в которой одно тело достаточно далеко удалено от других двух тел, закон 1/𝑟 будет выполняться, если квант поля имеет целый спин, и величина потенциала будет пропорциональна количеству вещества в удалённом теле. Эти туманности, которые до сих пор не влияли на наши физические законы, могут играть важную роль в гравитационном взаимодействии!

Тем не менее, для того, чтобы построить такую теорию, мы должны были бы предположить существование бозона с нулевой массой, который взаимодействует квадратично со всей остальной материей во вселенной, и должны были бы вернуться к вопросу, почему сила в точности пропорциональна массе. Но кажется, что нет смысла следовать по такому извилистому пути, когда мы не достигли цели с использованием известных частиц. Если предположить существование новой частицы, мы можем построить абсолютно хорошую теорию, предполагая существование частицы с нулевой массой и со спином 2, которая взаимодействует линейно с веществом.

Лекция 3

3.1. Спин гравитона

Ранее мы обсуждали с точки зрения воображаемых венерианских учёных возможные интерпретации гравитации на языке известных полей. Мы предполагаем, что эти учёные знают общие свойства различных вариантов теории поля; они пытаются отыскать поля, обладающие характеристиками гравитации. Для того, чтобы сделать различие между разными возможностями, нам необходимо вспомнить следующие свойства гравитации; что большие массы притягивают с силой, пропорциональной инерции и обратно пропорциональной квадрату расстояния; также, что масса и инерция характеризуют значение энергии, так что энергия связи атомов и ядер имеет гравитационное поведение, аналогичное энергии покоя.

Мы можем представить себе, что одна группа теоретиков, специалистов по теории поля, пыталась интерпретировать гравитацию в терминах известных частиц, как мы это делали на предыдущей лекции, и эта попытка провалилась. Другая группа теоретиков, специалистов по теории поля, начала выводить некоторые свойства нового поля, которое вело бы себя как гравитация.

Во-первых, обнаруживается, что гравитация обладает дальнодействием, что автоматически означает, что энергия взаимодействия зависит от расстояния как 1/𝑟. Не существует другой подобной возможности в теории поля. Это поле переносится посредством обмена частицей, которую ниже будем называть гравитоном. Она должна иметь массу 𝑚=0, так что сила, пропорциональная 1/𝑟², следует из из данного взаимодействия. Следующая догадка, которую мы должны сделать перед тем, как мы сможем начать работать в теории поля, состоит в том, что необходимо определить спин гравитона. Если спин равен 1/2 или полуцелый, то мы столкнёмся с трудностями, которые обсуждались в последней лекции (разделе 2.3), и где не было обнаружено интерференции между амплитудами одиночного обмена и не было обмена взаимодействием. Таким образом, спин гравитона должен быть целым, т.е. некоторое число из последовательности 0, 1, 2, 3, 4, … . Любое из этих значений спина давало бы взаимодействие, пропорциональное 1/𝑟, так как радиальная зависимость определяется исключительно массой. Для того, чтобы выбрать между различными возможными значениями спина, мы должны посмотреть на более тонкое различия между эффектами, обусловленными гравитонами с различными значениями спина. Мы можем себе представить, что наша группа теоретиков, специалистов по теории поля, разделила между собой эту работу так, что одни вывели возможные заключения из гипотезы, что спин равен нулю, другие анализировали возможность того, что спин равен 1, другие, что спин равен 2, 3 или даже 4. Затраты труда, связанные с обсуждением деталей теории для более высоких значений спина, значительно больше, чем для более низких значений спина, так что мы будем обсуждать эти значения в порядке возрастания.