𝑚₁β₁

+

𝑚₂β₂

=

𝑚₁

β

₁

+

𝑚₂

β

₂

,

в котором величина β₁ отрицательна в случае указанных на этом рисунке направлений движения. Чёрточки над буквами означают, что соответствующие величины взяты после соударения. Рассмотрим теперь этот же процесс в системе отсчёта ракеты. При малой относительной скорости движения ракеты β_𝑟 скорость каждой частицы в системе отсчёта ракеты находится путём простого вычитания β_𝑟 из скорости этой частицы в лабораторной системе отсчёта. Примените ньютоновский закон сохранения импульса к столкновению с точки зрения системы отсчёта ракеты. Покажите, что если ньютоновский импульс сохраняется в лабораторной системе отсчёта, он будет автоматически сохраняться и в системе отсчёта ракеты, движущейся с малой скоростью относительно лабораторной системы отсчёта.

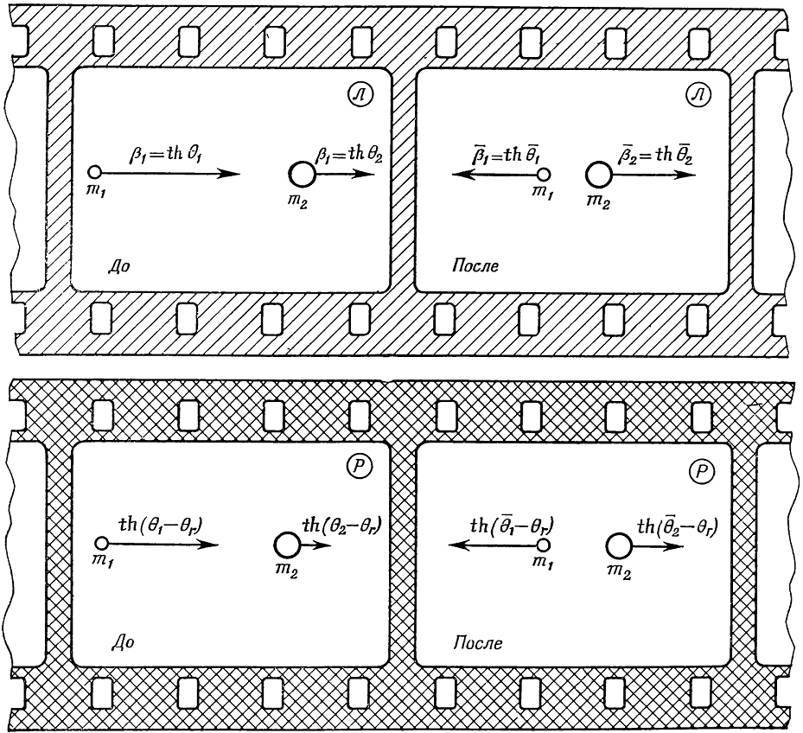
Рис. 103. Анализ упругого лобового столкновения частиц разных масс в релятивистской механике. Скорости частиц до и после соударения в лабораторной системе отсчёта (верхний рисунок) и в системе отсчёта ракеты (нижний рисунок), найденные по релятивистскому закону сложения параметров скорости.

б) Из сохранения релятивистского импульса следует сохранение релятивистской энергии. Рассмотрим теперь то же столкновение с релятивистской точки зрения. Покажите, что закон сохранения релятивистского импульса в лабораторной системе отсчёта выражается уравнением

𝑚₁ sh θ₁

+

𝑚₂ sh θ₂

=

𝑚₁ sh

θ

₁

+

𝑚₂ sh

θ

₂

.

(111)

При этом массы обеих частиц остаются неизменными, так как столкновение является упругим. В случае указанных на рис. 103 направлений движения величина θ₁ отрицательна. В релятивистской механике скорости частиц в системе отсчёта ракеты могут быть найдены путём вычитания параметра относительной скорости θ_𝑟 из параметра скорости этих частиц в лабораторной системе отсчёта (см. стр. 69). Примените закон сохранения импульса к этому столкновению, рассматриваемому в системе отсчёта ракеты. Используйте данные табл. 8 (стр. 77—78) для того, чтобы преобразовать все гиперболические синусы, зависящие от разностей параметров скорости. В полученном уравнении перегруппируйте члены, объединяя те из них, которые содержат ch θ_𝑟 или sh θ_𝑟:

(Скобка № 1)

⋅

ch θ

_𝑟

-

(Скобка № 2)

⋅

sh θ

_𝑟

=

0.

(112)

Величины, стоящие в скобках, уже не зависят от параметра относительной скорости θ_𝑟. Если теперь потребовать, чтобы импульс сохранялся в системе отсчёта любой ракеты, то полученное уравнение должно выполняться при всех значениях параметра относительной скорости θ_𝑟. Мы можем взять систему ракеты с любым значением параметра скорости — от нуля (когда ch θ_𝑟=1 и sh θ_𝑟=0) и до бесконечности (когда ch θ_𝑟 равняется sh θ_𝑟). Но полученное уравнение может выполняться при всех значениях θ_𝑟 в указанных пределах, лишь если каждая из скобок по отдельности равна нулю. Покажите, что скобка № 1 равняется нулю, если импульс сохраняется в лабораторной системе отсчёта. Покажите, что скобка № 2 равняется нулю, если

𝑚₁ ch θ₁

+

𝑚₂ ch θ₂

=

𝑚₁ ch

θ

₁

+

𝑚₂ ch

θ

₂

.

(113)

Уравнение (112) выражает закон сохранения импульса в системе отсчёта ракеты. Очевидно, что импульс сохраняется в системах отсчёта всех возможных ракет тогда и только тогда, когда в лабораторной системе одновременно выполняются уравнения (111) и (113). Уравнение (111) выражает закон сохранения импульса в лабораторной системе отсчёта. Какой же закон сохранения выражает уравнение (113)? Выясните смысл величины 𝑚 ch θ и назовите новый закон сохранения.

в) Останется ли справедливым приведённый вывод, если обозначить массы покоя частиц после столкновения через 𝑚₁ и 𝑚₂ и допустить, что они отличны от масс покоя частиц до столкновения? Будет ли оставаться верным закон сохранения релятивистской энергии и в этом случае? Сохраняется ли при таких столкновениях релятивистская кинетическая энергия? ▼

Б. ЭКВИВАЛЕНТНОСТЬ ЭНЕРГИИ И МАССЫ ПОКОЯ

62. Задачи на пересчёт

а) Сколько массы излучает 100-ваттная электрическая лампочка (в форме теплоты и света) в течение года?

б) В Соединённых Штатах в год вырабатывается около 10¹² квт⋅час электроэнергии. Чему равен массовый эквивалент этой энергии? В самом ли деле это количество массы превращается в энергию в процессе генерирования электроэнергии? Может быть, превращается меньшее или большее количество массы? Мотивируйте свой ответ.

в) Когда студент изо всех сил крутит педали велосипеда, он производит ½ лошадиной силы полезной мощности (1 л.с. = 746 вт). Коэффициент полезного действия человеческого организма составляет около 25%; это значит, что 75% пищи сгорает, превращаясь в теплоту, и лишь 25% пищи при сгорании переводится в полезную работу. Сколько времени должен ехать студент на велосипеде, чтобы потерять 1 кг массы за счёт её превращения в энергию? Почему же для уменьшения веса полезна физкультура?

г) На квадратный метр поверхности, перпендикулярной направлению солнечных лучей, вблизи Земли, но вне её атмосферы, от Солнца приходит около 1,4 квт световой энергии. (Эти 1,4 квт/м² носят название солнечной постоянной). Какое количество массы излучает Солнце в форме света в одну секунду? Сколько массы с Солнца поступает в форме света на Землю в год?

д) Два товарных поезда, каждый массой 10⁶ кг, движутся друг другу навстречу по одному и тому же пути с одинаковыми скоростями 45 м/сек (примерно 160 км/час). При столкновении они останавливаются. Масса покоя поездов в сумме с массами покоя рельсов и насыпи сразу же после столкновения возрастает; сколько микрограмм составляет это возрастание? Пренебрегите потерями энергии в форме звука и света. ▼

63. Релятивистская химия

При соединении 1 кг водорода 8 кг кислорода выделяется около 10⁸ дж энергии. Очень хорошие химические весы могут обнаружить относительное изменение массы, равное 10⁻⁷. Во сколько раз такая чувствительность больше (или меньше) необходимой для обнаружения относительного изменения массы в данной реакции? ▼

64**. Релятивистский осциллятор

Рис. 104. Электрон в качестве колеблющегося груза в релятивистском осцилляторе.

Для того чтобы проверить законы теории относительности, некий инженер решил построить осциллятор с очень лёгким колеблющимся грузом, способным очень быстро двигаться взад и вперёд. Самым лёгким из известных грузов с ненулевой массой покоя является электрон. Инженер взял кубический ящик из металла, каждое ребро которого равно 1 м, и слегка его подогрел, чтобы из стенок «испарилось» небольшое число электронов (рис. 104). Поперёк ящика в середине его помещена электрически изолированная от стенок металлическая сетка, к которой от генератора подведено высокое положительное напряжение. Ручку регулятора напряжения можно поворачивать, чтобы менять постоянную разность потенциалов 𝑉₀ между стенками ящика и сеткой.