и

𝑡'

=-

β

_𝑟

𝑥+𝑡

.

(58)

Теперь, исходя из обыденных нерелятивистских ньютоновских соображений, выведите формулы преобразования, связывающие между собой две системы отсчёта. Это преобразование называется преобразованием Галилея и выражается формулами

𝑥'

=

𝑥-𝑣

_𝑟

𝑡

_сек

(59)

(собственно преобразование Галилея) и

𝑡

_сек

'

=

𝑡

_сек

.

(60)

Здесь 𝑣_𝑟 — скорость относительного движения двух систем отсчёта, выраженная в метрах в секунду.

Может показаться, что формулы (57) и (58) и формулы (59) и (60) полностью противоречат друг другу. Справедливо ли это первое впечатление, а если нет, то почему? [Обсуждение. Почему в преобразовании Галилея (59) скорость 𝑣_𝑟 заменяет величину β_𝑟 из формулы (57)? Какой вид принимает формула (58), если подставить в неё величины 𝑣_𝑟 и 𝑡_сек? Как соотносятся друг с другом обыденные скорости и скорость света?] ▼

39*. Пределы применимости преобразования Галилея

Перейдите к более точному приближению в записи формул преобразования Лоренца при малых относительных скоростях, сохранив члены порядка θ_𝑟², но продолжая пренебрегать членами более высоких порядков. (Это —«второе приближение по θ_𝑟». Обратите внимание на то, что, согласно табл. 8, разложение th θ_𝑟 даже во втором порядке по θ_𝑟 даёт β_𝑟≈θ_𝑟). Покажите, что и в этом улучшенном втором приближении коэффициенты при 𝑥 и 𝑡 согласуются с соответствующими коэффициентами в формулах (57) и (58) с точностью, превышающей 1%, если скорости β_𝑟 ниже чем ¹/₇.

Если гоночный автомобиль может при постоянном ускорении с места набрать за 7 сек скорость 60 миль/час (около 27 м/сек), то за сколько дней (приблизительно) он достигнет при том же ускорении скорости β=1/7? За сколько дней можно достичь этой скорости при наивысшем ускорении, переносимом человеческим организмом в течение длительных периодов времени (около 7 𝑔, т.е. при семикратном ускорении свободного падения)? ▼

40*. Столкновения в теории Ньютона и в теории относительности. Область, в которой обе теории совпадают друг с другом с точностью до 1 %

Рис. 53. Изображение симметричного упругого рассеяния в лабораторной системе отсчёта. (Обратите внимание на разную штриховку кадров в лабораторной системе отсчёта и системе отсчёта ракеты!).

Пусть протон 𝐴 подвергается упругому столкновению с протоном 𝐵, первоначально находившимся в покое. Результат такого столкновения невозможно предсказать, так как мы не указали, насколько протоны сблизились при столкновении (а от этого зависит исход). При большинстве столкновений протон 𝐴 отклонится от первоначального пути лишь на малый угол α_𝐴, а протон 𝐵 при этом ощутит лишь слабый толчок в сторону под углом α_𝐵 (относительно направления движения протона 𝐴), близким к 90°. Но может произойти и очень тесное сближение протонов, когда почти вся энергия передаётся протону 𝐵, и он вылетает под весьма малым углом α_𝐵 к направлению «вперёд» (первоначальному пути 𝐴). Промежуточными случаями по отношению к этим двум крайностям являются происходящие время от времени столкновения с «симметричным рассеянием», когда обе (тождественные) частицы разлетаются с одинаковыми скоростями в направлениях, образующих равные углы, α_𝐴=α_𝐵=α/2, с направлением «вперёд» (рис. 53). Вопрос: чему равен угол отклонения частиц при симметричном рассеянии? Обсуждение. По механике Ньютона полный угол разлёта одинаковых частиц равен 90° при всяком упругом столкновении (будь то симметричное рассеяние или нет!). То, что этот угол при столкновениях быстрых частиц оказывается менее 90°, есть одно из самых интересных и доказательных предсказаний теории относительности. На рис. 54б дана фотография «медленного» столкновения, при котором, в согласии с теорией Ньютона, угол разлёта равен 90°. Напротив, на рис. 54а представлен случай «быстрого» столкновения, при котором угол разлёта частиц явно меньше 90°. Этот факт означает, что отличие угла разлёта от 90° даёт хороший критерий отклонения законов движения от ньютоновских. Рассмотрим, например, такой вопрос: ниже какого значения должна быть скорость частицы в подобном опыте по рассеянию, для того чтобы величина угла разлёта частиц отклонялась от 90° менее чем на ¹/₁₀₀ радиана? Решение этой задачи значительно упрощается, если подойти к случаю описанного выше симметричного рассеяния, выбрав систему отсчёта таким образом, чтобы можно было максимально воспользоваться соображениями симметрии. Сядем для этого в ракету и полетим направо как раз с такой скоростью, которая равна компоненте «вперёд» скорости каждой из частиц после рассеяния. Тогда при наблюдении с этой ракеты частицы 𝐴 и 𝐵 не будут испытывать движения в направлении движения ракеты после столкновения. Что же касается боковых компонент скорости частиц 𝐴 и 𝐵 (в направлениях вверх и вниз), то заметим, что эти скорости были равны по абсолютной величине и противоположны по направлению в лабораторной системе отсчёта. Но ведь такая симметрия скоростей не может измениться, если мы наблюдаем теперь столкновение с ракеты, летящей вправо. Поэтому и при наблюдении в системе отсчёта ракеты скорости частиц 𝐴 и 𝐵 после столкновения будут равны по абсолютной величине и противоположны по знаку. Это тот вывод № 1, которым мы обязаны соображениям симметрии. Вывод № 2 из соображений симметрии также может быть получен при анализе столкновения в системе отсчёта ракеты. Он гласит, что в этой системе до столкновения скорости частиц 𝐴 и 𝐵 также были равны по абсолютной величине и противоположны по направлению. Почему? Какое противоречие ожидало бы нас, если бы эти скорости не были равными? — Да просто нарушилась бы сама симметрия, что легко усмотреть из следующего.

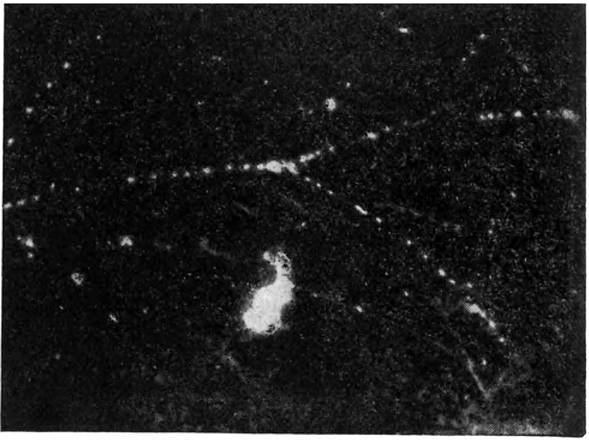
Рис. 54а. Сделанная в камере Вильсона фотография релятивистского и почти симметричного рассеяния, когда первоначально один электрон двигался, а другой покоился.

Начальная скорость первого электрона около β=0,97. Угол между треками разлетающихся электронов много меньше, чем предсказывавшиеся ньютоновской механикой 90°. Искривление треков электронов как заряженных частиц вызвано присутствием магнитного поля, с помощью которого определялись импульсы электронов.

Рис. 546. Фотография нерелятивистского симметричного упругого рассеяния, когда первоначально один протон двигался, а другой покоился. Начальная скорость первого протона около β=0,1. Угол между треками разлетающихся протонов равен 90° в согласии с ньютоновской механикой.

Схема скоростей в системе отсчёта ракеты после столкновения характеризуется симметрией между правым и левым направлениями. Иными словами, глядя на частицы, разлетающиеся после столкновения, невозможно сказать, из каких направлений пришли эти частицы в точку соударения. С равным успехом частица 𝐴 могла прийти слева, а 𝐵 — справа, или частица 𝐴 — справа, а 𝐵 — слева (например, наблюдатель мог обойти арену и посмотреть с другой стороны). Но ведь участвующие в столкновении частицы тождественны друг другу, и ничего не должно измениться, если их взаимно переименовать.