⎛

⎜

⎝

25 м × 25 м × 25 м

пространства

⎞

⎟

⎠

×

⎛

⎜

⎝

21⋅10⁸ м

времени

⎞

⎟

⎠

Обсуждение областей пространства-времени, размеры которых превышают размеры таких локальных инерциальных систем, см. в гл. 3.

Определение пробной частицы

«Пробная частица». Насколько мала должна быть частица для того, чтобы её можно было принять за пробную? Её масса должна быть настолько малой, чтобы присутствие этой частицы в пределах некоторой заданной степени точности не влияло на движение других близких к ней частиц. На языке ньютоновской механики это означает, что гравитационное притяжение между пробной частицей и другими частицами должно быть пренебрежимо малым (с заданной степенью точности). Рассмотрим, например, частицу с массой 10 кг. Если поместить другую частицу с меньшей массой в ¹/₁₀ м от неё, то первоначальное состояние покоя этой второй частицы нарушится настолько, что она сдвинется менее чем за 3 мин на 10⁻³ м. Итак, 10-килограммовый объект не есть пробная частица в этой смысле. Пробная частица подвергается действию гравитационных сил, но сама не вызывает появления сколько-нибудь заметной гравитационной силы.

Рис. 7. Новейшая инерциальная система отсчёта. Вырезка из журнала Engineering Opportunities за март 1964 г.

СТРОИТЕЛЬСТВО

В прошлом месяце был предложен подряд на строительство нулевого цикла 500-футовой башни свободного падения, обеспечивающей условия невесомости на период до 10 сек, в Льюисовском исследовательском центре НАСА в Кливленде. Пролёт свободного падения высотой около 400 фут обеспечит пятисекундный период невесомости. Пневматическое поршневое устройство на дне шахты позволит подбрасывать образцы в 6000 фунт весом и 4 фут в диаметре до вершины башни, продлевая тем самым период невесомости до 10 сек. Для торможения образцов будет использован пенопласт. Система вакуумных насосов позволит поддерживать в шахте давление, соответствующее высоте около 50 миль, так что отпадает необходимость окружать образец экранами, компенсирующими сопротивление воздуха. Сооружение будет использовано для исследований жидких и газообразных систем в условиях невесомости в рамках проблемы запуска жидкостных двигателей в условиях космоса в ходе орбитальных полётов. Функционирующая в настоящее время в Льюисе малая башня свободного падения обеспечивает невесомость лишь на период от 2 до 4 сек и допускает испытания образцов лишь 10 дюйм в диаметре.

Инерциальную систему удаётся ввести, потому что все тела падают с одним и тем же ускорением

Инерциальную систему отсчёта было бы невозможно определить, если бы не существовало замечательного природного феномена. Все частицы различных размеров, формы и состава падают в одном и том же месте с одним и тем же ускорением относительно Земли. Если бы это было не так, наблюдатель внутри падающего космического корабля заметил бы относительное ускорение у разных частиц, даже когда эти частицы находятся вблизи друг друга. По крайней мере некоторые из частиц, покоившихся первоначально, вышли бы из состояния покоя, что означало бы непригодность космического корабля как инерциальной системы отсчёта согласно определению последней. В какой мере мы уверены в том, что все частицы в одном и том же месте, но разные по своему составу падают на Землю с одним и тем же ускорением? Как говорит легенда, Галилей бросал для проверки этого предположения с «Падающей башни» в Пизе шары, сделанные из разных веществ ¹). В 1922 г. барон Роланд фон Этвёш установил с точностью 5:10⁹, что дерево и платина испытывают одинаковое ускорение со стороны Земли. Недавно Роберт Дикке указал, что Солнце является более удобным источником гравитационного ускорения для измерений (см. упражнение 35). Изменение каждые 12 час направления солнечного притяжения на противоположное позволяет производить фантастически большое усиление путём резонанса. Цилиндры из алюминия и золота подвергались ускорению со стороны Солнца (0,59⋅10⁻² м/сек²), одинаковому с точностью 3:10¹¹, как показали Р. Дикке и Питер Ролл ²). Это была одна из наиболее чувствительных проверок фундаментальнейшего физического принципа: тождества ускорения, вызванного силой тяжести у пробной частицы любой природы.

¹) О том, производил ли в действительности Галлией этот эксперимент, см. книгу Lloyd W. Taylor, Phisics the Pioneer Science, Vol. 1, Dover Publications, New York, 1959, p. 25.

²) См. главу по эксперименту в теории относительности, написанную Дикке в книге Relativity, Groups, and Topology, ed. by C. and B. DeWitt, Gordon and Breach, New York, 1964, p. 173—177, или в книге R.H. Diсke, The Theoretical Significance of Experimental Relativity, Gordon and Breach, New York, 1964.

Из этого принципа вытекает, что для выяснения, является ли данная система отсчёта инерциальной, в качестве пробной частицы может быть использована частица, состоящая из любого вещества. Система отсчёта, инерциальная для пробных частиц одного вида, будет также инерциальной для пробных частиц любых других видов.

3. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ

Перекрывающиеся инерциальные системы отсчёта движутся относительно друг друга прямолинейно и равномерно

Мы описываем движение пробных частиц по отношению к некоторой системе отсчёта, с тем чтобы выяснить, является ли эта система инерциальной. Движения тех же пробных частиц, а также их столкновения (если таковые происходят) могут быть описаны и по отношению более чем к одной инерциальной системе. Носителем одной системы отсчёта может быть космический корабль, выполненный в форме полого цилиндра (рис. 8, а), тогда как носителем другой системы отсчёта может быть подобная же конструкция с несколько меньшим диаметром, таким, чтобы при встрече с первой она могла пролететь внутри неё (рис. 8, б). При этом существует область пространства-времени, общая для внутренней части обоих кораблей во время их взаимного совмещения. Множество пробных частиц могут пролетать в том или ином произвольно выбранном направлении через эту область. Путь каждой из них будет прямолинейным, если изобразить его в координатах одной из систем отсчёта, а также в координатах другой, так как они обе являются инерциальными системами отсчёта. Такая прямолинейность путей возможна лишь благодаря тому, что любые две перекрывающиеся друг с другом инерциальные системы отсчёта движутся друг относительно друга равномерно. Напротив, если второй космический корабль включает двигатели и ускоряется во время прохождения сквозь первый (рис. 8, в), то по наблюдениям с этого второго корабля траектории пробных частиц будут искривлены. Если имеющееся оборудование позволяет заметить кривизну таких траекторий, то эту ускоренную систему отсчёта нельзя считать инерциальной.

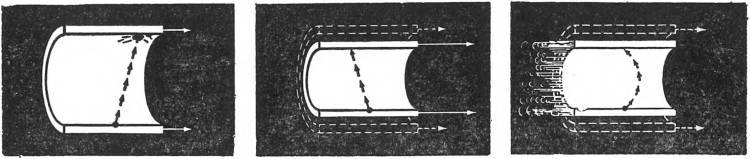
а) Движение типичной пробной частицы, наблюдаемое в первой инерциальной системе.

б) Движение той же частицы, наблюдаемое во второй инерциальной системе отсчёта, движущейся относительно первой.

в) Движение той же пробной частицы, наблюдаемое в ускоренной, а потому неинерциальной системе отсчёта.

Рис. 8. Сравнение инерциальных систем отсчёта с ускоренной системой.

Если даны две инерциальные системы отсчёта, равномерно движущиеся друг относительно друга, то любая находящаяся в движении пробная частица будет относительно них сохранять величину и направление скорости своего движения неизменными, хотя бы даже эти величина и направление её скорости были совершенно различными в каждой из двух систем. В самом деле, ведь мы определили понятие инерциальной системы отсчёта так, чтобы в любой инерциальной системе был справедлив следующий закон механики (первый закон Ньютона): «Всякое тело сохраняет состояние покоя или прямолинейного равномерного движения, пока и поскольку оно не понуждается внешними силами изменить это состояние». Кроме этого закона механики, существуют и другие. Каждый из них также будет справедлив в любой инерциальной системе отсчёта, о чём свидетельствует эксперимент.