Понятие инерциальной системы отсчёта

Взглянем на свободно падающий космический корабль с поверхности Земли. Мы увидим, как проста причина того, что первоначально покоившаяся свободная частица сохраняет своё состояние покоя относительно корабля. Причина эта в том, что по отношению к поверхности Земли как корабль, так и частица падают с одним и тем же ускорением (рис. 4). Именно благодаря такому равенству ускорений относительные положения частицы и космического корабля не меняются, если наша частица первоначально покоилась относительно корабля.

Рис. 5. Железнодорожный вагон, свободно падающий в горизонтальном положении вблизи Земли.

В определении инерциальной системы отсчёта содержится требование, чтобы в ней не ощущались гравитационные силы. Если в качестве такой системы взят космический корабль, находящийся вблизи Земли, то он не должен быть очень большим, так как помещённые в него на большом расстоянии друг от друга частицы будут испытывать разное воздействие со стороны неоднородного гравитационного поля Земли. Так, если двум частицам с разных концов корабля предоставить возможность свободно падать, каждая из них будет притягиваться к центру Земли, и они будут сближаться друг с другом в ходе падения (рис. 5). В качестве другого примера возьмём две частицы, раздвинутые в вертикальном направлении, строго одна над другой (рис. 6). Их ускорение под действием силы тяжести будет иметь одно и то же направление, но более близкая к Земле частица будет мало-помалу оставлять другую позади, и по мере падения космического корабля расстояние между частицами будет увеличиваться. В обоих случаях законы механики не будут простыми в очень большом космическом корабле — большой космический корабль не представляет собой инерциальной системы отсчёта.

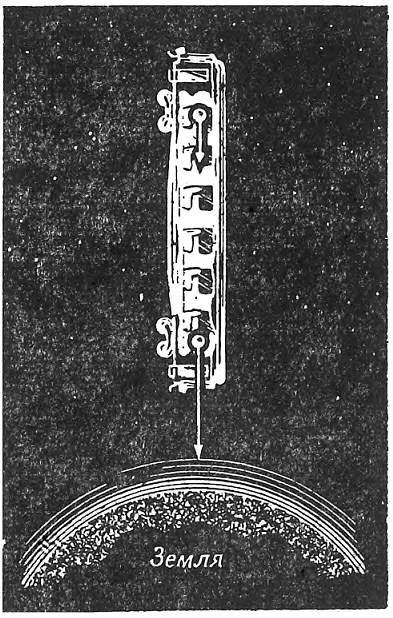
Рис. 6. Железнодорожный вагон, свободно падающий в вертикальном положении вблизи Земли.

Земное притяжение неоднородно, и большой космический корабль не может служить инерциальной системой отсчёта

Однако нам нужно, чтобы законы механики имели в космическом корабле простой вид. Поэтому необходимо устранить все относительные ускорения, вызванные внешними факторами, «устранить» в том смысле, чтобы сделать величину этих ускорений ниже обнаружимого предела, когда они уже не будут искажать картины более важных ускорений, подлежащих изучению (например, возникающих при столкновении частиц). Это может быть достигнуто при выборе достаточно малого космического корабля. Чем меньше космический корабль, тем меньше и величина относительных ускорений объектов в разных точках этого корабля. Пусть мы располагаем приборами, измеряющими относительные ускорения с любой заданной степенью точности. Как бы высока ни была точность (чувствительность) этих приборов, мы можем всегда взять космический корабль настолько малых размеров, что эти паразитные относительные ускорения окажутся ниже предела чувствительности приборов. В рамках выбранной точности такой космический корабль можно считать инерциальной системой отсчёта.

Пример космического корабля, имеющего достаточно малые размеры, чтобы быть пригодным в качестве инерциальной системы, отсчета

Когда можно сказать, что космический корабль или другая лаборатория имеет размеры достаточно малые, чтобы его можно было назвать инерциальной системой отсчета? Иначе говоря, когда относительные ускорения свободных частиц, помещенных в разных концах лаборатории, слишком малы, чтобы быть наблюдаемыми? Разбор ситуации в какой-то одной лаборатории послужит иллюстрацией для наших рассуждений. Допустим, что железнодорожный вагон 25 м длины в горизонтальном положении сброшен с высоты 250 м на поверхность Земли (рис. 5). Время, прошедшее от начала до конца падения, будет равно приблизительно 7 сек, т.е. около 21⋅10⁸ м светового времени. Пусть в первый момент падения в воздухе в противоположных концах вагона будут предоставлены самим себе два маленьких шарика от подшипника. За время падения они приблизятся друг к другу на 10⁻³ м (толщина 10 страниц этой книги) под действием различия в направлениях действующей на них силы земного притяжения (см. упражнение 32). В другом случае предположим, что тот же вагон сбрасывается в вертикальном положении, причем нижний его конец вначале находится на высоте 250 м над поверхностью Земли (рис. 6). Вновь освободим при этом в противоположных концах вагона два шарика от подшипника. Теперь за время падения шарики удалятся друг от друга на 2⋅10⁻³ м, так как нижний из них испытывает большее гравитационное ускорение, чем верхний. В каждом из этих примеров будем считать, что используемые в вагоне измерительные приборы не обладают достаточной чувствительностью, чтобы зафиксировать относительное движение шариков. Тогда, пользуясь приборами указанной степени чувствительности и в указанные ограниченные сроки наблюдения, мы можем принять наш железнодорожный вагон (или рассмотренный прежде свободно падающий космический корабль) в качестве инерциальной системы отсчёта. Повысив чувствительность измерительного оборудования, мы уже не сможем использовать данный космический корабль в качестве инерциальной системы отсчёта, если не изменим постановку опыта. Для этого следует либо укоротить 25-метровый отрезок, на котором проводились наблюдения, либо сократить длительность последних во времени. Лучше всего, однако, сократить в некоторой согласованной комбинации как пространственные, так и временные размеры исследуемой области. Наконец, как последнюю альтернативу можно предложить отправить с помощью ракеты (часть «в» упражнения 32) всю систему в такую область пространства, где невозможно измерить «дифференциал гравитационного ускорения» между двумя противоположными концами вагона. Эту же мысль можно выразить иначе: ускорение частиц относительно вагона должно стать нечувствительно малым. Эти относительные ускорения могут быть измерены внутри вагона без привлечения каких-либо внешних наблюдений. И только если эти относительные ускорения слишком малы, чтобы быть замеченными, существует система отсчёта, относительно которой законы движения имеют простой вид,— инерциальная система отсчёта.

Определение инерциальной системы отсчёта

Система отсчёта называется инерциальной в некоторой области пространства и времени, если во всей этой области пространства-времени с некоторой данной степенью точности любая первоначально покоившаяся пробная частица сохраняет своё состояние покоя, а любая пробная частица, первоначально двигавшаяся, продолжает своё движение без изменения величины и направления своей скорости. Инерциальную систему отсчёта называют также лоренцевой системой отсчёта. При таком определении инерциальные системы всегда с необходимостью локальны, т.е. инерциальны лишь в ограниченной области пространства-времени.

Определение области пространства-времени

«Область пространства-времени»— каков точный смысл этого понятия? Длинный и узкий железнодорожный вагон, использованный в нашем примере, служил средством для исследования пространства-времени на ограниченном отрезке времени и в том или ином пространственном направлении. Его можно было направить с севера на юг, с востока на запад либо сверху вниз. При каждой ориентации могло быть измерено относительное ускорение двух маленьких шариков от подшипника, освобождённых в противоположных концах вагона. Как можно показать с помощью вычислений, во всех трёх направлениях (как и в промежуточных) относительный «дрейф» этих двух пробных частиц составлял половину (или менее) минимальной поддающейся обнаружению величины. Тогда во всём кубе с рёбрами 25 м пространства и на протяжении 7 сек времени всевозможными способами движущиеся пробные частицы отклоняются от прямолинейного движения на не поддающуюся обнаружению величину. Другими словами, данная система отсчёта является инерциальной в области пространства-времени с размерами