Один электронвольт есть то количество энергии, которое необходимо, чтобы перенести одну частицу с элементарным зарядом 𝑒 через разность потенциалов 1 вольт
Что такое 1 АЕМ? Возьмём 12 г 𝙲¹², разделим на 𝑁 и получим величину массы одного атома 𝙲¹²; по определению она равна 12 АЕМ. Следовательно, 1 AEM = 1/𝑁 г
↓
↓
Умножение на
𝑁
Умножение на
𝑁
↓
↓
𝑁 электронвольт есть та энергия, которая необходима, чтобы перенести 𝑁 элементарных зарядов через разность потенциалов 1 вольт
𝑁 атомных единиц массы, выраженных в единицах массы, эквиваленты 1 г или 0,001 кг
↓
↓
т.е. та энергия, которая необходима, чтобы перенести 1 моль электричества через разность потенциалов 1 вольт
а выраженные в единицах энергии эквиваленты 𝑚𝑐²=(0,001 кг) ⋅[(2,997925±0,000003)⋅10⁸ м/сек]²
↓
↓
или та энергия, которая необходима, чтобы перенести количество электричества, равное фарадееву электрохимическому эквиваленту (96487,0±1,6 кулон), через разность потенциалов 1 вольт: 96487,0±1,6 джоулей
т.е. эквивалентны (8,987554±0,000009)⋅10¹³ джоулей
↓
↓
Это 𝑁 электронвольт
Это 𝑁 атомных единиц массы
↘
↙
следовательно, 1 электронвольт эквивалентен
96487,0±1,6
(8,987554±0,000009)⋅10¹³
или (1,073562±0,000017)⋅10⁻⁹ АЕМ (относительная ошибка равна 1,6⋅10⁻⁵)
↓
т.е. 1 АЕМ эквивалентна (0,931478±0,000015)⋅10³ Мэв
В этих вычислениях масса ядра трития выступает как вывод, полученный при анализе законов сохранения, сопоставленный и подтверждённый методами масс-спектроскопии. Этот пример подтверждения физики пространства-времени впечатляет, и после него невозможно уже сомневаться в том, что энергия массы покоя способна превращаться в кинетическую энергию.
Тем не менее всё ещё может быть непонятным, как это такой простой принцип смог породить столь сложное равенство, как (99), которое мы применили для вывода массы ядра трития. Почему мы не взяли просто определённые спектрометрическим путём массы реагентов, такие же массы продуктов реакции и не сравнили их с балансом кинетической энергии при этом превращении? Что могло бы быть проще этого?!
Реагенты:
𝙷²
2.0141019
АЕМ
𝙷²
2.0141019
АЕМ
Сумма:
4,0282038
АЕМ
Продукты реакции:
𝙷¹
1,0078252
АЕМ
𝙷³
3,0160494
АЕМ
Сумма:
4,0238746
АЕМ
Разность:
0,0043292
АЕМ
Энергетический эквивалент:
4,0322546
Мэв
Трудность возникает лишь на следующем этапе, когда требуется определить из наблюдений полный выход кинетической энергии. Кинетическая энергия дейтрона, находившегося до реакции в движении, известна и равна 1,808 Мэв, тогда как кинетическая энергия протона после реакции равна 3,467 Мэв.
Однако при этом затруднительно измерять кинетическую энергию получающегося ядра трития, и эта энергия не измерялась. Но если неизвестна кинетическая энергия одного из продуктов реакции, то это значит, что не проводилось непосредственного измерения полного выхода кинетической энергии. Как же можно тогда сопоставить выход энергии при реакции с изменением масс покоя реагентов? Сводится ли на самом деле такое сравнение к какому-то непосредственному сопоставлению двух энергий? — Нет.
Измеряются кинетические энергии не всех частиц. Простое сравнение энергий невозможно
Можно составить ложное представление о происходящих явлениях, если думать, что они исчерпываются энергетическими переходами. При геодезической съёмке возможна столь же ошибочная концепция. Так, земельный план является многоугольником хитрой формы, наложенным на поверхность, которая не является плоской. Требуется найти длину прямолинейной границы 𝐴, а землемер измерил лишь разность координат по линии север — юг для 𝐴 и 𝐵. Если его воображение неспособно на большее, то он встанет в тупик! Подобным же образом безнадёжно определять массу ядра трития из приведённых выше данных для дейтрон-дейтронной реакции, основываясь лишь на энергиях. Необходимо учесть также баланс импульсов.
Определение массы ядра трития аналогично определению длины наклонной стороны многоугольника
Рис. 93. Определение массы ядра трития с помощью законов сохранения, рассматриваемое как геометрическая задача. Учтите: точки 𝑂, 𝐵, 𝐶 лежат в плоскости чертежа; точка 𝐴 лежит выше плоскости чертежа (𝑦-компонента импульса).
Массу ядра трития находят, пользуясь законами сохранения, подобно тому как землемер находит длину стороны многоугольника из ряда измерений на этом многоугольнике, пользуясь эвклидовой геометрией (рис. 93). Между этими двумя случаями имеется лишь одно существенное различие — в физике необходимо исходить из лоренцевой геометрии. Поэтому мы получим
(
𝑚₃
)
²
=
(
𝐸
-компонента
𝐴𝐵
)
²
-
(
𝑝
-компонента
𝐴𝐵
)
²
.
Энергетическая и импульсная компоненты стороны 𝐴𝐵 в этой формуле определяются по энергетическим и импульсным компонентам других трёх сторон многоугольника, т.е. по данным о других трёх частицах. Как найти значения 𝐸 и 𝑝 для одной из этих частиц, например для налетающего дейтрона? Ответ: с помощью процедуры, изображённой на рис. 94 и не похожей на обычно используемую при съёмках земельных планов! Предположим, что от землемера требовалось бы использовать метод, аналогичный применённому в опыте с реакцией 𝙷²+𝙷²→𝙷¹+𝙷³. Сделать это он мог бы, лишь воспользовавшись следующей необычной процедурой для нахождения компонент граничной прямой 𝐶𝐵 в направлениях север — юг и восток — запад (см. рис. 94, переводя его с языка физики частиц на язык геодезии!): 1) Измерение длины прямой 𝐶𝐵. 2) и 3) Измерение компоненты этого отрезка в направлении север — юг. 4) Использование теоремы Пифагора для нахождения компоненты отрезка 𝐶𝐵 в направлении восток — запад.
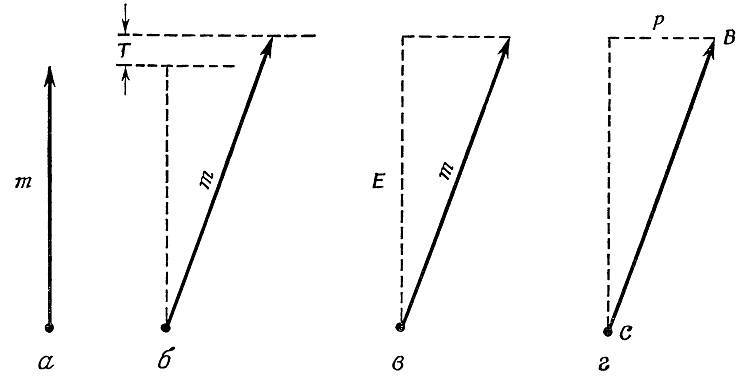
Рис. 94. Экспериментальное определение энергии и импульса как компонент 4-вектора энергии-импульса в опыте по соударению дейтронов, 𝙷²+𝙷²→𝙷¹+𝙷³. (Обозначение концов вектора через 𝐵 и 𝐶 — использование тех же обозначений, что и на рис. 93).
а — масса покоя (определённая с помощью масс-спектрометра);
б — кинетическая энергия (определяемая разностью потенциалов, через которую пропущены бомбардирующие дейтроны);
в — сумма энергии покоя и кинетической энергии (из соотношения 𝐸=𝑚+𝑇);
г — импульс (из соотношения 𝑝²=𝐸²-𝑚²).
Теперь мы разобрали, как определяются компоненты векторов энергии-импульса дейтрона-мишени (на рис. 93 отрезок 𝑂𝐶), налетающего дейтрона (𝐶𝐵) и выбитого протона (𝑂𝐴). Компоненты неизвестной четвёртой стороны многоугольника (отрезок 𝐴𝐵, соответствующий ядру трития) могут быть тогда найдены путём простого комбинирования трёх других известных 4-векторов — вычисления, начинающегося магической формулой «применим законы сохранения импульса и энергии»: