𝑥'=0,

𝑡'=τ

_π

.

Как воспримет эти события наблюдатель в лаборатории? Сколько времени проживёт π-мезон с момента своего рождения до смерти по его часам, т.е. чему равен промежуток лабораторного времени 𝑡? Какое расстояние пройдёт π-мезон за период своей жизни, т.е. чему равно лабораторное расстояние 𝑥 от точки его образования в верхних слоях атмосферы до той точки внизу, где он распался? Короче говоря, пусть некоторое событие 𝐸 определяется в системе ракеты заданными значениями координат 𝑥' и 𝑡' относительно начала 𝑂. Как определить тогда координаты 𝑥 и 𝑡 того же самого события относительно того же самого начала в лабораторной системе отсчёта (рис. 25, а)?

Такой вопрос для нас нов. До сих пор мы рассматривали при описании относительного положения событий лишь инвариантный интервал. Величина такого интервала не зависит от выбора системы отсчёта, причём

⎛

⎜

⎜

⎝

Пространствен-

ноподобный

интервал

⎞²

⎟

⎟

⎠

=-

⎛

⎜

⎜

⎝

Времен-

ноподобный

интервал

⎞²

⎟

⎟

⎠

=

=

𝑥²-𝑡²

=

(𝑥')²-(𝑡')²

.

(15)

В разных системах отсчёта координаты события различны

Сосредоточим теперь наше внимание на самих координатах как характеристике расположения события 𝐸 относительно начала 𝑂. Мы сделаем это, заранее признавая, что они зависят от выбора системы отсчёта. В этом отношении положение координат гораздо менее универсально, чем положение инвариантного интервала как меры взаимного разделения событий. Пусть так. Физика должна приладиться к тому, что есть в мире. Описывать удалённость событий друг от друга следует тем методом, который лучше соответствует обстоятельствам. Бывает, что торпедному катеру полезнее указать, что расстояние между носом и кормой атакуемого судна 50 м. Но в другом случае может быть, что ему гораздо важнее указать, что положение носа судна относительно кормы 40 м к северу и 30 м к востоку. В той задаче, которая нас занимает, нам не интересно, что мировая точка распада π-мезона отстоит от мировой точки его образования на величину инвариантного интервала τ, равную около 10⁻⁸ сек. Нам нужно охарактеризовать удалённость этих событий друг от друга самими координатами 𝑥 и 𝑡.

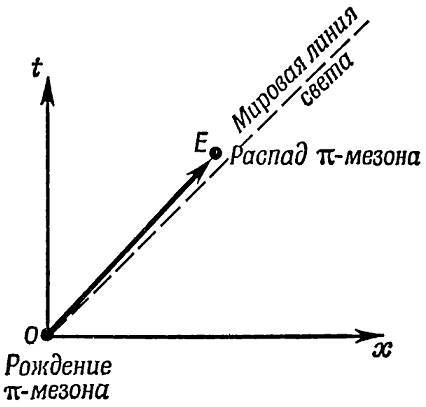
а) Диаграмма пространства-времени лабораторной системы отсчёта.

б) Диаграмма пространства-времени системы отсчёта ракеты.

Рис. 25. Координаты точек рождения (точка 𝑂) и распада (точка 𝐸) π-мезона, изображённые на диаграммах пространства-времени лабораторной системы и системы отсчёта ракеты.

Преобразование Лоренца для координат

Как бы сильно ни различались координаты (𝑥',𝑡') события 𝐸 в системе отсчёта ракеты от его координат (𝑥,𝑡) в лабораторной системе, эти два набора координат связаны друг с другом вполне определённым и простым законом. Этот закон выражается через преобразование Лоренца

𝑥

=

𝑥'

√1-β_𝑟²

+

β_𝑟𝑡'

√1-β_𝑟²

,

𝑡

=

β_𝑟𝑥'

√1-β_𝑟²

+

𝑡'

√1-β_𝑟²

,

(16)

где β_𝑟— скорость системы отсчёта ракеты относительно лабораторной системы отсчёта. Ввиду выполнения этого закона говорят, что координаты обеспечивают ковариантное описание взаимной удалённости событий в пространстве-времени в противоположность инвариантному описанию этой удалённости, обеспечиваемому интервалом. Корень «вари» в слове ковариантный»

Определение понятия «ковариантность»

указывает, что координаты изменяются (варьируют) при переходах от одной системы отсчёта к другой. Приставка «ко» означает, что преобразование координат всех событий производится по одному и тому же закону (координированно). Итак, для разных событий различны как координаты 𝑥' и 𝑡', так и координаты 𝑥 и 𝑡, но четвёрка коэффициентов

⎛

⎝

1-β

_𝑟

²

⎞-½

⎠

,

β

_𝑟

⋅

⎛

⎝

1-β

_𝑟

²

⎞-½

⎠

,

β

_𝑟

⋅

⎛

⎝

1-β

_𝑟

²

⎞-½

⎠

,

⎛

⎝

1-β

_𝑟

²

⎞-½

⎠

,

связывающая эти два набора координат, обладает значениями, не зависящими от того, какое событие рассматривается.

В этом разделе мы будем обсуждать вывод формул преобразования Лоренца, их использование и их сходство с известными формулами преобразований эвклидовой геометрии, иллюстрируемыми на примере притчи о землемерах.

Три принципа, на которых основано преобразование Лоренца

Вывод преобразования Лоренца основывается на трех принципах, которые мы уже можем сформулировать:

1) Коэффициенты преобразования не должны зависеть от того, какое событие рассматривается («ковариантность преобразования»).

2) Выбор коэффициентов преобразования должен соответствовать тому, что точка, фиксированная в системе отсчета ракеты, движется в лабораторной системе отсчета со скоростью β_𝑟 в положительном направлении оси 𝑥.

3) Коэффициенты преобразования должны быть такими, чтобы любой интервал имел одно и то же значение в лабораторной системе и в системе отсчета ракеты.

Эти три принципа легко применить к случаю распада π-мезона. В лабораторной системе отсчета это событие имеет координаты (𝑥,𝑡) относительно события — рождения мезона, и эти координаты должны быть выражены через скорость β_𝑟 системы отсчета ракеты, в которой π-мезон покоится. Эту скорость непосредственно даёт отношение координат 𝑥 и 𝑡,

𝑥

𝑡

=

β

_𝑟

,

так что

𝑥

=

β

_𝑟

𝑡

,

или

𝑥²

=

β

_𝑟

²

⋅

𝑡²

.

(17)

Первый этап вывода преобразования Лоренца

Временноподобный интервал, образованный 𝑥 и 𝑡, определяется временем жизни π-мезона в системе отсчёта ракеты (где мезон покоится в точке 𝑥'=0):

𝑡²-𝑥²

=

𝑡'²-𝑥'²

=

𝑡'²-0

=

τ

_π

²

.

Подставим в эту формулу β_𝑟²𝑡² вместо 𝑥² на основании уравнения (17). Получим

𝑡²

-

β

_𝑟

²𝑡²

=

𝑡'²

=

τ

_π

²

,

или

𝑡²

=

𝑡²

1-β_𝑟²

=

τ_π²

1-β_𝑟²

,

или