𝑡
=
𝑡'
√1-β𝑟²
=
τπ
√1-β𝑟²
.
(Численный пример: положим β𝑟=¹²/₁₃ скорости света; тогда 1-β𝑟²=1-¹⁴⁴/₁₆₉=²⁵/₁₆₉ и (1-β²)⁻¹/²=¹³/₅=2,6. Следовательно, время жизни π-мезона, измеренное в лаборатории, в 2,6 раза длиннее «собственного времени жизни», т.е. оно в 2,6 раза длиннее, чем время жизни, измеренное в системе отсчёта, связанной с самим мезоном). Расстояние, пройденное π-мезоном, равно времени движения, умноженному на скорость, так что
𝑥
=
β
𝑟
𝑡
=
β𝑟𝑡'
√1-β𝑟²
.
Решение задачи о π-мезоне
Этим расчётом завершается решение поставленной задачи (найти координаты мировой точки распада π-мезона относительно мировой точки его рождения в лабораторной системе координат).
Задача о π-мезоне служила введением к общей задаче — найти координаты данного события в лабораторной системе, если заданы его координаты в системе ракеты. Если мы покажем, что эта задача равнозначна выводу формул преобразования Лоренца, значит, мы пришли к методу вывода этого преобразования, исходя из простейших предположений. На самом деле, мы уже нашли два коэффициента из четырёх в формулах преобразования Лоренца:
𝑡
=
β
𝑟
𝑡
=
𝑡'
√1-β𝑟²
+
𝐴𝑥'
,
𝑥
=
β
𝑟
𝑡
=
β𝑟𝑡'
√1-β𝑟²
+
𝐵𝑥'
.
Что касается остальных двух коэффициентов, временно обозначенных через 𝐴 и 𝐵, то о них мы ничего не узнали просто потому, что π-мезон всё время покоился в точке 𝑥'=0 в системе ракеты. Благодаря этому коэффициенты 𝐴 и 𝐵 могли иметь любые конечные значения при одном и том же решении
Конечный этап вывода преобразования Лоренца
задачи о мезоне. Чтобы найти значения этих коэффициентов, мы перейдём от специального случая (события — распада 𝐸) к более общему случаю — событию, происходящему в точке с произвольными координатами 𝑥' и 𝑡'. Мы вновь потребуем, чтобы величина интервала была одинаковой в лабораторной системе и в системе отсчёта ракеты. Другими словами, потребуем выполнения равенства
𝑡²-𝑥²
=
𝑡'²-𝑥'²
,
или
⎡
⎢
⎣
𝑡'
√1-β𝑟²
+
𝐴𝑥'
⎤²
⎥
⎦
-
⎡
⎢
⎣
β𝑟𝑡'
√1-β𝑟²
+
𝐵𝑥'
⎤²
⎥
⎦
=
𝑡'²-𝑥'²
,
или
𝑡'²
+
2(𝐴-β𝑟𝐵)𝑥'𝑡'
√1-β𝑟²
+
(𝐴²-𝐵²)
𝑥'²
=
𝑡'²
-
𝑥'²
.
(18)
Это равенство не может выполняться для всевозможных 𝑡' и 𝑥', если только коэффициенты 𝐴 и 𝐵 не выбраны вполне определённым образом. Во-первых, эти коэффициенты должны быть такими, чтобы в левой части равенства (18) обратился в нуль множитель при 𝑥'𝑡' (так как в правой части подобного члена нет). Тогда
𝐴
=
β
𝑟
𝐵
.
Во-вторых, множители при (-𝑥'²) в левой и правой частях равенства (18) должны совпадать. Поэтому
𝐵²
-
𝐴²
=
1.
Мы получили два уравнения для двух неизвестных 𝐴 и 𝐵; решая их, найдём
𝐴
=
β𝑟
√1-β𝑟²
и
𝐵
=
1
√1-β𝑟²
Этим вычислением и завершается вывод формул преобразования Лоренца (16).
Роль преобразования Лоренца
Новый — ковариантный — подход имеет дело с компонентами пространственно-временного интервала — координатами 𝑥, 𝑡 (16), а не с величиной самого интервала (15). Язык интервалов подобен универсальному языку: любой интервал одинаков для наблюдателей во всех системах отсчёта. Напротив, компоненты взаимного удаления событий в пространстве-времени, измеренные в одной системе отсчёта,— это весьма частный язык для выражения такого удаления. По своей форме этот язык похож на тот частный язык, с помощью которого та же удалённость описывается в другой системе отсчёта. Ведь в обоих языках фигурируют «пространственные» и «временная компоненты». Но само по себе это обстоятельство ещё ничего не даёт для сравнения информации, которой располагают разные группы наблюдателей. Когда англичанин берёт турецкую газету, ему не легче от знания того, что в турецком языке, как и в английском, есть глаголы и существительные! Ему нужен ещё и словарь. Так вот для перевода на свой язык информации о пространственных и временных координатах событий из других систем отсчёта наблюдателю тоже требуется словарь. Этот словарь — формулы преобразования Лоренца (16).
Аналогия: землемеры пользуются преобразованием эвклидова пространства
Подобный же словарь необходим и при гораздо более обычных обстоятельствах. Дневной землемер, определяющий север по магнитному компасу, может перевести на свой язык измерения северной и восточной координат, сделанные ночным землемером, ориентирующимся по Полярной звезде. Но не потребуется никакого словаря, если они будут сравнивать свои результаты, выраженные на универсальном языке расстояний. Бросается в глаза различие между двумя методами — исходящим из инвариантов (расстояния — универсальный язык) и использующим компоненты (северную и восточную координаты, величины которых, определённые разными наблюдателями, различны). Эту противоположность инвариантных и ковариантных величин иллюстрирует рис. 26.
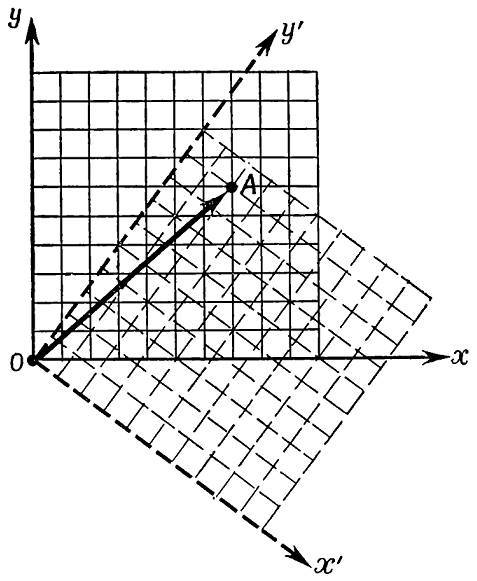
Рис. 26. Ковариантный подход к геометрии использует компоненты величин, например компоненты вектора 𝑂𝐴. (Напротив, в инвариантном подходе используются длины, например длина 𝑂𝐴. Такие длины имеют численные значения, не зависящие от выбора системы отсчёта. Иначе говоря, любая длина одинакова независимо от того, кто её определяет — землемер, определяющий направление на север по Полярной звезде, или землемер, пользующийся магнитным компасом).
Пусть в одной системе значения компонент равны (𝑥,𝑦)=(7,6), а в другой системе — (𝑥',𝑦')=(2,9). (Эти числа соответствуют нашему чертежу). Очевидно, что значения компонент в двух системах отсчёта различны. В самом деле, они связаны законом «ковариантного преобразования» 𝑥 =
4
5 𝑥' +
3
5 𝑦' , 𝑦 =-
3
5 𝑥' +
4
5 𝑦' ,
который в частном случае вектора 𝑂𝐴 записывается в виде 7 =
4
5 •2 +
3
5 •9 , 6 =-
3
5 •2 +
4
5 •9 ,
Приведённые здесь конкретные численные значения коэффициентов в законе преобразования связаны с тем конкретным поворотом, который изображён на чертеже.
В притче о землемерах студент сделал, как теперь обнаруживается, лишь полдела. Он выяснил, как должен каждый землемер переводить свои результаты на универсальный язык расстояний:
(Расстояние)
²
=
(
Δ
𝑥)²
+
(
Δ
𝑦)²
=
=
(
Δ
𝑥')²
+
(
Δ
𝑦')²
.