Проверка инерциальности системы отсчёта, образованной данной решёткой

По движению пробных частиц сквозь решётку часов, а говоря точнее, по регистрациям совпадений, отпечатанным нашими хронографами, мы можем выяснить, представляет ли собой эта решётка инерциальную систему отсчёта. Если зарегистрировано, что: а) пробная частица (с некоторой заданной точностью) последовательно проходит мимо часов, расположенных на прямой линии; б) скорость β пробной частицы, вычисленная по этим же записям, постоянна (вновь с некоторой заданной степенью точности) и в) такие выводы получаются для стольких мировых линий пробных частиц, сколько их сможет проследить в данной области пространства и времени самый трудолюбивый наблюдатель, то эта решётка часов образует в данной области пространства-времени инерциальную систему отсчёта.

Лабораторная система отсчёта и система ракеты при совпадении 𝑥-осей

Мы снова описали движение пробных частиц относительно конкретной системы отсчёта с целью определить, является ли данная система инерциальной. Одни и те же пробные частицы, а в случае их столкновений одни и те же акты соударения могут быть описаны как по отношению к одной инерциальной системе отсчёта, так и по отношению к другой. Пусть две системы отсчёта реализуются двумя разными решётками из метровых стержней и часов, так что одна система движется относительно другой равномерно, а оси 𝑥 обеих систем совпадают. Назовём одну из этих систем отсчёта лабораторной, а другую, движущуюся относительно первой в положительном направлении оси 𝑥, — системой отсчёта ракеты (рис. 10 и 11). Ракета летит с выключенным двигателем с постоянной скоростью относительно лаборатории. Пусть решётки ракеты и лаборатории перекрываются в том смысле, что имеется область пространства, общая для обеих систем отсчёта (как это описано в разд 3 и показано на рис. 8). В этой общей области пространства-времени движутся пробные частицы. По их движению, зарегистрированному часами данного наблюдателя, этот наблюдатель удостоверяется в том, что его система отсчёта инерциальна; пусть это имеет место для наблюдателей в обеих системах отсчёта.

Рис. 10. Лабораторная система отсчёта и система ракеты. Соответствующие им решётки были наложены друг на друга секунду назад.

Рис. 11. Лабораторная система отсчёта (слева) п система ракеты (справа) —дальнейшая схематизация рис. 10. В обеих системах заштрихованы центральные опорные часы.

Наблюдатели в лаборатории и на ракете фиксируют одно и то же событие

Взорвём хлопушку. Её взрыв будет зарегистрирован ближайшими к нему часами лабораторной решётки; он будет также зарегистрирован ближайшими к месту взрыва часами решётки ракеты. Как связаны между собой записи о координатах взрыва у часов-хронографов в лаборатории и на ракете? Частично на этот вопрос сразу же отвечает принцип относительности: в записях часов в лаборатории и на ракете будет указано одно и то же значение координаты 𝑦. Для доказательства предположим, что часы-хронограф на ракете снабжены кистью, смоченной в краске, и делают отметки на лабораторной решётке при своём движении. Это изображено на рис. 12 для случая, когда 𝑦=1 м. Эти отметки на лабораторной решётке служат для нахождения лабораторной координаты 𝑦, соответствующей 𝑦=1 у часов на ракете. Эти отметки ложатся на лабораторные часы с 𝑦=1, не выше и не ниже их. Ведь если бы краска ложилась на стержни решётки ниже лабораторных часов с 𝑦=1, то оба наблюдателя заключили бы, что часы на ракете с 𝑦=1 прошли «ниже» лабораторных часов с 𝑦=1. Цепочка отметок краской сделала бы этот факт очевидным для всех. Аналогично, если бы эти отметки ложились на стержни выше лабораторных часов с 𝑦=1, то оба наблюдателя заключили бы, что часы на ракете с 𝑦=1 прошли «над» лабораторными часами с 𝑦=1. В обоих случаях имелась бы возможность экспериментально отличить друг от друга эти две системы отсчёта. Но ведь отличить эти системы друг от друга с помощью какого-либо другого эксперимента было невозможно — в принципе относительности содержится утверждение, что такого экспериментально находимого различия между инерциальными системами отсчёта вообще не может быть. Отсюда мы заключаем, что отличить эти две системы отсчёта невозможно и с помощью этого эксперимента. Поэтому координата 𝑦 любого события, и в том числе взрыва, с которого мы начали этот абзац, будет одной и той же как в системе отсчёта ракеты, так и в лабораторной системе.

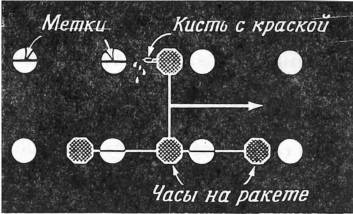
Рис. 12. Доказательство того, что координата 𝑦 любого события одинакова в лабораторной системе отсчёта и в системе ракеты.

Координата 𝑦 события одинакова как в лабораторной системе отсчёта, так и в системе ракеты

Из аналогичных доводов следует, что и координата 𝑧 любого события одинакова как в системе отсчёта ракеты, так и в лабораторной системе. Заметим, что обе эти координаты события — и 𝑦, и 𝑧 — отсчитываются в направлении, перпендикулярном направлению относительного движения наших систем отсчёта.

Координата 𝑧 события одинакова как в лабораторной системе отсчёта, так и в системе ракеты

Тот факт, что длины, измеренные поперёк направления относительного движения систем отсчёта, одинаковы, сразу же даёт возможность сравнивать ход часов в обеих решётках. Пусть световая вспышка бегает, отражаясь между двумя зеркалами, установленными в системе отсчёта ракеты на опорных часах и на часах, расположенных в точке с координатой 𝑦=1 точно над опорными часами. Такая вспышка будет возвращаться в исходную точку через 2 м светового времени системы ракеты. Траекторию этого светового луча можно проследить и в лабораторной системе вверх до того же самого значения координаты 𝑦 и снова вниз до опорных часов. Учитывая, что скорость света в обеих системах одинакова, можно вычислить лабораторное время, соответствующее времени распространения света по двухметровому замкнутому пути в системе отсчёта ракеты. В следующем параграфе этот расчёт приведёт к заключению об инвариантности интервала.

5. ИНВАРИАНТНОСТЬ ИНТЕРВАЛА

Какая мера характеризует относительное расположение событий 𝐴 и 𝐵 и одинакова во всех инерциальных системах отсчёта?

Расстояние между двумя городскими воротами определяется по значениям разностей координат 𝑥 этих ворот и по значениям разностей их координат 𝑦. Как определить аналогичную физическую величину — пространственно-временной интервал между двумя событиями? Между какими двумя событиями определяется такой интервал?

Пусть событие 𝐴 — акт излучения световой вспышки. Пусть событие 𝐵 — акт приёма этой вспышки после того, как она была отражена другим объектом. Эти два акта можно назвать парой событий. Нас не интересуют сами по себе ни свет, ни отражающий его объект. Однако анализ траектории светового луча в пространстве-времени позволяет легко и быстро найти величину (тот самый интервал), которая связана с этой парой событий и значение которой одинаково во всех инерциальных системах отсчёта.

Событие 𝐴 — акт излучения вспышки

Событие 𝐵 — акт приёма вспышки

Событие 𝐴 — лампа даёт вспышку. Её свет распространяется к отражателю 𝑅 (рис. 13), от которого он снова идёт вниз. Событие 𝐵 — приём вспышки. Рассмотрим теперь подробности согласно рис. 13.

а) Путь светового луча, наблюдаемый в лабораторной системе отсчёта.

б) Путь светового луча, наблюдаемый в системе отсчета ракеты.

в) Путь светового луча, наблюдаемый в системе отсчета сверхракеты.

Рис. 13. Испускание, отражение и приём опорной вспышки (приём происходит в начале координат в системе отсчёта ракеты).