Физическая интерпретация. Из анализа соотношения (6.33) мы можем получить некоторые физические характеристики движения. За промежуток времени 𝑇 электрон проходит полное расстояние, равное 𝑅_𝑎+𝑅_𝑏. Следовательно, его скорость в течение этого промежутка времени составляет 𝑢=(𝑅_𝑎+𝑅_𝑏)/𝑇, его энергия равна 𝑚𝑢²/2, а импульс равен 𝑚𝑢. При этом мы предполагаем, что энергия электрона не изменяется в процессе рассеяния. То, что эти значения скорости, энергии и импульса совместимы друг с другом, можно проверить, рассмотрев вид экспоненциального множителя перед интегралом в формуле (6.33). Фаза этого экспоненциального фактора равна 𝑖𝑚[(𝑅_𝑎+𝑅_𝑏)²/2ℏ𝑇], поэтому частота, определяемая производной этой фазы по переменной 𝑇, составляет

ω=

𝑚

2ℏ

(𝑅_𝑎+𝑅_𝑏)²

𝑇²

.

(6.34)

Если скорость 𝑢 определена так, как это сделано выше, то энергия будет равна 𝑚𝑢²/2 [ср. соотношение (3.15)].

Дифференцирование фазы по переменной 𝑅_𝑎 даёт волновое число в точке 𝑎

𝑘

=

𝑚

ℏ

𝑅_𝑎+𝑅_𝑏

𝑇

(6.35)

а это значит, что величина импульса равна 𝑚𝑢 [ср. соотношение (3.12)].

Задача 6.5. Интеграл по переменной 𝑡 в формуле (6.28) можно аппроксимировать, используя метод стационарной фазы. Рассмотрите этот метод на примере данного интеграла; покажите, что наибольший вклад в интеграл дают значения 𝑡 из области, близкой к точке 𝑡=𝑅_𝑎/𝑢 и представляющей собой время, за которое электрон должен был бы достигнуть центра атома, если бы он двигался по классическим законам.

Используя определение скорости электрона 𝑢=(𝑅_𝑎+𝑅_𝑏)/𝑇, запишем вектор импульса входящей частицы 𝐩_𝑎 в виде

𝐩

_𝑎

=

𝑚𝑢

𝐢

_𝑎

,

(6.36)

а вектор импульса выходящей частицы 𝐩_𝑏 — как

𝐩

_𝑏

=

𝑚𝑢

𝐢

_𝑏

.

(6.37)

Тогда соотношение (6.33) можно представить в виде

𝐾

⁽¹⁾

(𝑏,𝑎)

=

-

𝑖

ℏ

⎧

⎪

⎩

𝑚

2π𝑖ℏ

⎫5/2

⎪

⎭

𝑢

𝑇^½𝑅_𝑎𝑅_𝑏

⎡

⎢

⎣

exp

⎧

⎪

⎩

𝑖𝑚

2ℏ

𝑢²𝑇

⎫

⎪

⎭

⎤

⎥

⎦

×

×

_𝑟

∫

⎧

⎨

⎩

exp

⎡

⎢

⎣

𝑖

ℏ

(𝐩

_𝑎

-𝐩

_𝑏

)⋅𝐫

⎤

⎥

⎦

⎫

⎬

⎭

𝑉(𝐫)

𝑑³𝐫

.

(6.38)

Обозначим далее изменение (или передачу) импульса через

𝐪

=

(𝐩

_𝑎

-𝐩

_𝑏

)

и введём величину

𝑣(𝐪)

=

_𝑟

∫

𝑒

^{(𝑖/ℏ)𝐪⋅𝐩}

𝑉(𝐫)

𝑑³𝐫

.

(6.39)

Вероятность того, что электрон достигнет точки 𝑎, даётся квадратом модуля ядра 𝐾_𝑉(𝑏,𝑎) и, следовательно, будет зависеть в основном от первого члена разложения этого ядра, т.е. от величины 𝐾₍₀₎(𝑏,𝑎), которая, по-видимому, настолько велика, что полностью перекрывает малый возмущающий член 𝐾⁽¹⁾(𝑏,𝑎).

Поэтому в большинстве экспериментов по рассеянию обычно коллимируют входящий пучок соответствующими экранами, с тем чтобы те электроны, которые не рассеиваются на атомах мишени, не выходили бы за пределы ограниченной области вдоль некоторого направления, как это показано на фиг. 6.6. Конечно на таких коллимирующих экранах будет происходить дифракция (как это уже обсуждалось нами в гл. 3, § 2 и 3), и вне области центрального пучка будет наблюдаться некоторое число нерассеянных электронов. Однако коллиматоры можно установить таким образом, чтобы для точек, достаточно удалённых от оси коллимации, число дифрагировавших на коллиматоре электронов было бы очень мало по сравнению с числом электронов, рассеянных на атомах мишени.

Фиг. 6.6. Принципиальная схема фокусировки для исключения влияния члена нулевого порядка в точке 𝑏.

В этом случае из точки 𝑎 в точку 𝑏 с заметной вероятностью могут прийти лишь те электроны, которые испытывают хотя бы одно рассеяние. Поэтому член нулевого порядка в разложении 𝐾_𝑉(𝑏,𝑎) в ряд теории возмущений будет вносить лишь пренебрежимо малый вклад и его можно отбросить. Вклад возникает за счёт члена первого порядка 𝐾⁽¹⁾(𝑏,𝑎).

Тогда вероятность обнаружения электрона в такой области, по крайней мере в первом порядке теории возмущений, определяется только квадратом модуля ядра 𝐾⁽¹⁾(𝑏,𝑎). Используя соотношения (6.38) и (6.39), запишем эту вероятность как

𝑃(𝑏)

ед. объёма

=

1

ℏ²

⎧

⎪

⎩

𝑚

2π𝑖ℏ

⎫5

⎪

⎭

𝑢²

𝑇𝑅²_𝑎𝑅²_𝑏

|𝑣(𝐪)|²

.

(6.40)

Характерные особенности атомного потенциала и зависимость ядра от относительных направлений векторов 𝑅_𝑎 и 𝑅_𝑎 заключены в этой формуле в множителе 𝑣(𝐪). Этот множитель совершенно не зависит от размеров экспериментального устройства; их влияние учитывается остальной частью формулы (6.40). Например, множитель 1/𝑅²_𝑎, как легко видеть, обусловлен тем, что вероятность столкновения электрона с атомом убывает обратно пропорционально 𝑅²_𝑎. Может показаться, что в применении к рассматриваемому эксперименту это утверждение спорно из-за наличия коллиматоров. Однако эффект коллимации пренебрежимо мал на расстояниях порядка атомных размеров; по отношению к атому-мишени пучок налетающих электронов состоит из частиц, изотропно испускаемых некоторым точечным источником. Точно так же изотропно по всем направлениям от рассеивающего атома разлетаются и рассеянные электроны. Поэтому отнесённая к единице объёма вероятность регистрации электрона в точке 𝑏 изменяется обратно пропорционально 𝑅²_𝑏. Поскольку наиболее интересные свойства рассматриваемого эксперимента связаны с функцией 𝑣(𝐪) мы уделим этой функции особое внимание в следующем параграфе.

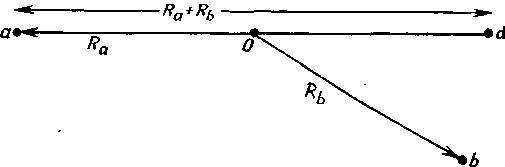
Фиг. 6.7. Сравнение точек 𝑏 и 𝑑.

Если точки 𝑏 и 𝑑 находятся на одинаковых расстояниях от точки 𝑂, равных 𝑅_𝑏 то различие в числе электронов, попадающих в эти точки, будет обусловленно лишь процессом рассеяния. Точка 𝑑 лежит на пути движения нерассеявшихся электронов. Отношение числа электронов, попавших в точку 𝑏, к числу электронов, которые достигли бы точки 𝑑 если бы на их пути не было рассеивающего центра, равно вероятности рассеяния в точку 𝑏.