𝑒
(𝑖/ℏ)𝐸2𝑡2
𝐾(𝐑
2
,𝑡
2
;𝐑
1
,𝑡
1
)
×
×
𝑒
(𝑖/ℏ)𝐩1⋅𝐑1
𝑒
-(𝑖/ℏ)𝐸1𝑡1
𝑑³𝐑
1
𝑑³𝐑
2
𝑑𝑡
1
𝑑𝑡
2
.
(5.13)
Заметим, что энергия 𝐸 здесь не равна 𝑝²/2𝑚, а является дополнительным аргументом (коэффициентом, на который умножается время), необходимым для определения ядра. Точное измерение величины 𝐸 для установления связи между энергией и импульсом можно сделать лишь в том случае, когда система бесконечно долго находится в состоянии с одной и той же энергией.
В качестве примера вычислим ядро для случая свободной частицы. Необходимые интегралы по переменным 𝐑1 и 𝐑2 были уже найдены и определяются формулой (5.12). Нам остаётся выполнить интегрирование лишь по 𝑡1 и 𝑡2. Сделаем подстановку 𝑡2=𝑡1+τ. Тогда двойной интеграл можно записать как
∞
∫
-∞
𝑒
-(𝑖/ℏ)(𝐸2-𝐸1)𝑡1
𝑑𝑡
1
∞
∫
0
𝑒
-(𝑖/ℏ)(𝐸2-𝑝²/2𝑚)τ
𝑑τ
.
(5.14)
Первый из этих двух интегралов является интегральным представлением δ-функции Дирака и равен 2πℏδ(𝐸2-𝐸1). Второй интеграл имеет вид
∞
∫
0
𝑒
𝑖ωτ
𝑑𝑡
.
(5.15)
Такие интегралы часто встречаются в квантовомеханических задачах; при действительном ω они расходятся. Поэтому для того, чтобы мы могли выполнить наш расчёт, заменим ω комплексным числом ω+𝑖ε. Когда обе величины ω и ε — действительные числа, интеграл равен 𝑖/(ω+𝑖ε).
Теперь можно было бы просто перейти к пределу этого выражения при ε, стремящемся к нулю, и принять за результат 𝑖/ω. Однако такой подход привёл бы нас к неправильным (или, точнее, к неполным) результатам в дальнейшем. Функция, которую мы вычисляем,— это ядро, и в дальнейшем её следует- проинтегрировать (после умножения на некоторую другую функцию) по всем значениям ω или по всем значениям другой некоторой эквивалентной величины. Если в нашем выражении опустить ε, то рассматриваемый интеграл имел бы полюс при значении ω=0.
Было бы неправильным брать в этом случае просто главную часть интеграла в точке такого полюса. Это дало бы нам неверный результат. В частности, обратное преобразование полученного ядра не привело бы снова к тому первоначальному координатному представлению ядра, из которого мы исходили. Результат преобразования отличался бы от исходного выражения тем, что не обращался бы в нуль при отрицательных значениях времени. Правильный результат для таких интегралов можно получить, если сдвинуть полюс на бесконечно малое расстояние выше действительной оси. Это и достигается введением в наше выражение величины ε.
Преобразовав выражение 𝑖/(ω+𝑖ε) к виду
𝑖(ω-𝑖ε)
ω²+ε²
=
𝑖ω
ω²+ε²
+
ε
ω²+ε²
,
(5.16)
можно первый член в правой части представить как 𝑖/ω и в дальнейшем интеграл от него вычислять в смысле главного значения. Второй член при ε, стремящемся к нулю, становится равным πδ(ω), так что в дальнейшем при интегрировании его следует учитывать именно в таком виде. Это означает, что если мы хотим более точно математически определить значение указанного интеграла, то выражение 𝑖/(ω+𝑖ε) должно быть заменено на 𝙿𝙿[(𝑖/ω)+πδ(ω)]. Другими словами,
∞
∫
0
𝑒
𝑖ωτ
𝑑𝑡
=
lim
ε→0
𝑖
ω+𝑖ε
=
𝙿𝙿
⎡
⎢
⎣
⎧
⎪
⎩
𝑖
ω
⎫
⎪
⎭
+πδ(ω)
⎤
⎥
⎦
.
(5.17)
В последующем во всех выражениях, содержащих ε, будет подразумеваться предельный переход при ε→0.
Возвращаясь к вычислению ядра, заменим ω на 𝐸2-(𝑝²/2𝑚), после чего получим
𝐸
0
(𝐩
2
,𝐸
2
;𝐩
1
,𝐸
1
)
=
(2πℏ)
4
δ³
(𝐩
2
-𝐩
1
)
δ(𝐸
2
-𝐸
1
)
×
×
⎧
⎪
⎩
𝐸
1
-
𝑝²1
2𝑚
+𝑖ε
⎫-1
⎪
⎭
.
(5.18)
Наличие δ-функций в этом выражении означает, что ни энергия, ни импульс 𝑝 не изменяются во время движения свободной частицы. Эти две величины, как это видно из последнего множителя, и определяют движение частицы.
Таким образом, амплитуда движения свободной частицы с энергией 𝐸 и импульсом 𝑝 из одной точки в другую пропорциональна 𝑖[𝐸-(𝑝²/2𝑚)+𝑖ε]-1.
В этой главе мы уже отмечали, что энергия 𝐸 здесь, вообще говоря, не равна 𝑝²/2𝑚, а является независимой переменной.
Чтобы понять, чем это обусловлено, рассмотрим ядро для свободной частицы, которое можно представить некоторой осциллирующей функцией в пространстве и времени, где величина 𝐸 является коэффициентом при переменной времени и, следовательно, обладает свойствами частоты. Ядро, заданное равенством (5.12), представлено на фиг. 5.4 как функция разности времён 𝑇=𝑡2-𝑡1. Оно обращается в нуль при отрицательном 𝑇 и начинает осциллировать при значении 𝑇=0. Преобразование от временного к энергетическому представлению эквивалентно преобразованию Фурье. Так как волна образуется сразу при 𝑇=0, то фурье-компонента определена при всех значениях частот и, следовательно, для всех энергий. Однако если функция рассматривается на большом временном интервале (много периодов), то в фурье-компоненте начинает преобладать лишь одна из частот. Для свободной частицы такая доминирующая частота соответствует энергии 𝐸0=𝑝²/2𝑚.
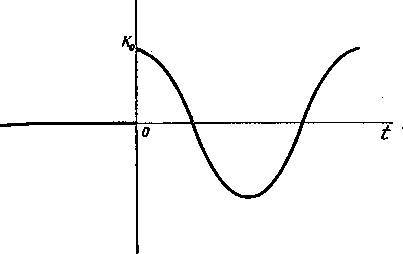
Фиг. 5.4. Действительная часть ядра 𝐾0 (описывающего движение свободной частицы) как функция времени.
Для отрицательных моментов времени эта функция обращается в нуль, в точке 𝑡=0 она скачкообразно возрастает, а далее имеет вид косинусоидальной волны с постоянной амплитудой и частотой.
Именно поэтому ядро в случае свободной частицы содержит множитель
𝑖
=𝙿𝙿
⎧
⎪
⎩
𝑖
⎫
⎪
⎭
+πδ
⎧
⎪
⎩
𝐸
2
1
-
𝑝²
2𝑚
⎫
⎪
⎭
.
𝐸
0
-𝑝
2
2𝑚+𝑖ε
𝐸
2
-𝑝²/2𝑚
1