Дальнейшее рассмотрение приводит нас к тому, что эта своеобразная связь является общим законом переходов между стационарными состояниями; мы должны предположить, что возможность перехода между двумя данными стационарными состояниями связана с наличием определённой гармонической компоненты в движении системы. Величина указанной компоненты может быть совершенно различной в двух рассматриваемых состояниях, когда числа 𝑛' и 𝑛'' невелики по сравнению с их разностью. Поэтому можно наперёд ожидать, что связь между вероятностью перехода и амплитудой гармонической компоненты движения будет, вообще говоря, сложной. То же самое можно сказать относительно связи частоты излучения и соответствующей компоненты движения. С этой точки зрения мы должны, например, рассматривать зелёную водородную линию 𝐻_β, отвечающую переходу из четвертого состояния во второе, некоторым образом как «октаву» красной линии 𝐻_α, соответствующей переходу из второго состояния в третье, хотя частота колебаний первой линии никоим образом не равна удвоенной частоте второй линии. Мы должны рассматривать процесс, вызывающий появление линии 𝐻_β как обусловленный наличием некоторой гармонической компоненты в движении атома, являющейся октавой к компоненте того движения, которая приводит к возможности излучения линии 𝐻_α.

Прежде чем переходить к рассмотрению других спектров, в которых мы найдём многочисленные применения изложенной точки зрения, я хочу упомянуть об одном интересном применении изложенных соображений к теории осциллятора Планка. Вычислим из формул (1) и (4) частоту колебаний, соответствующую переходу из одного особого состояния осциллятора в другое; мы найдём

ν

=

(𝑛'-𝑛'')ω

,

(13)

где 𝑛' и 𝑛'' - числа, определяющие указанные состояния. Существенная предпосылка теории Планка заключается в том, что частота поглощаемого и испускаемого осциллятором излучения всегда равна ω мы видим, что эта предпосылка равносильна утверждению, что в данном осцилляторе, в противоположность атому водорода, возможны только переходы между двумя соседними стационарными состояниями. С точки зрения, развитой выше, этого можно было ожидать, так как разница между осциллятором и атомом водорода, по нашему предположению, заключалась в том, что движение осциллятора, в противоположность движению электрона в атоме, является чисто гармоническим. Мы видим, таким образом, формальную возможность построить теорию излучения, в которой спектр водорода и простой спектр осциллятора Планка фигурировали бы совершенно равноправно. Однако, очевидно, что только для такой простой системы, как осциллятор, теория может быть сформулирована одним условием; в общем случае это условие распадается на два: одно, касающееся характера движения в стационарных состояниях, и другое, относящееся к частоте излучения, испускаемого при переходах между этими состояниями.

Переходя теперь к спектрам элементов с более высоким атомным номером, мы видим, что они имеют более сложное строение, чем спектр водорода. Однако, как известно, для спектров многих элементов найдены простые законы, представляющие собой замечательную аналогию с формулой Бальмера для спектра водорода. По Ридбергу и Ритцу, частоты колебаний сериальных спектров этих элементов могут быть выражены формулой типа

ν

=

𝑓

_𝑘''

(𝑛'')

-

𝑓

_𝑘'

(𝑛')

,

(14)

где 𝑛' и 𝑛'' — целые числа; 𝑓_𝑘'(𝑛') и 𝑓_𝑘''(𝑛'') — две функции, принадлежащие к ряду определённых функций, характерных для данного элемента, весьма просто зависящие от 𝑛 и, в частности, приближающиеся к нулю при больших значениях 𝑛. Оставляя первый член в правой части (14) постоянным и подставляя для 𝑛' во втором члене 𝑓_𝑘'(𝑛') различные последовательно возрастающие целые числа, мы получаем различные серии линий. Полный спектр может быть получен на основании так называемого комбинационного принципа Ритца, если в формуле (14) вместо 𝑓_𝑘'(𝑛'') и 𝑓_𝑘''(𝑛') подставлять все сочетания двух величин из совокупности всевозможных значений 𝑓_𝑘(𝑛).

То обстоятельство, что частота всякой спектральной линии является разностью двух простых выражений, зависящих от целых чисел, приводит, на основании нашей интерпретации процесса излучения, непосредственно к предположению о том, что члены в правой части равенства (14), умноженные на ℎ, могут быть приравнены энергии в различных стационарных состояниях атома. В спектрах других элементов, в противоположность спектру водорода, фигурирует не одна, но целый ряд функций 𝑛. Этот факт вынуждает нас признать для атомов этих элементов существование не одного, но нескольких рядов стационарных состояний; энергия 𝑛-го состояния 𝑘-го ряда может быть представлена (если опустить произвольную постоянную) в виде

𝐸

_𝑘

(𝑛)

=

-ℎ𝑓

_𝑘

(𝑛)

.

(15)

Подобную сложность совокупности стационарных состояний элементов с более высокими атомными номерами и следует ожидать на основании связи между спектрами, вычисленными по теории квантов, и разложением движений атома на гармонические колебания. Как мы уже видели, с этой точки зрения простота совокупности стационарных состояний атома водорода самым тесным образом связана с простым периодическим характером движения этого атома. В других элементах, где нейтральный атом содержит несколько электронов, мы находим более сложные движения и имеем более сложное разложение на гармонические колебания; установив связь между движениями атома и спектром, определяемым условием частот, мы должны ожидать и более сложной совокупности стационарных состояний. В дальнейшем мы увидим, как можно в деталях проследить такое соответствие и каким образом этот путь ведёт к непосредственному объяснению тех тёмных мест, которые были связаны с применением комбинационного принципа в связи с кажущимся произволом наличия или отсутствия линий, предсказываемых этим принципом.

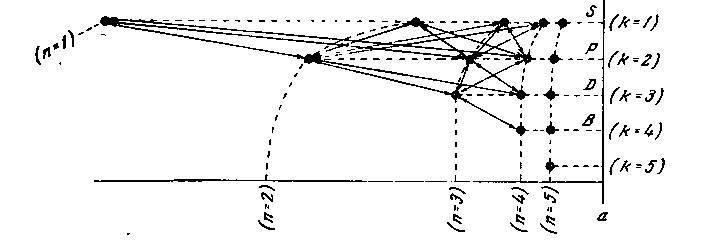
Рис. 1. Теоретическая схема образования сериального спектра натрия

На рис. 1 представлены те стационарные состояния, которые могут быть определены указанным образом для атома натрия. Состояния обозначены черными кружками, причём расстояния последних от вертикальной линии 𝑎𝑎 пропорциональны численному значению энергии, которая им отвечает. Стрелки на этой схеме обозначают переходы между состояниями, соответствующие тем линиям спектра натрия, которые получаются при обычных условиях возбуждения. Способ, которым расположены здесь состояния по горизонтальным рядам, полностью соответствует обычному расположению «спектральных» термов в спектроскопических таблицах. Состояния в первом горизонтальном ряду, обозначенные 𝑆, соответствуют переменному члену в выражении так называемой резкой побочной серии, излучаемой при переходах из этих состояний в первое состояние во второй строке. Состояния, обозначенные через 𝑃, соответствуют переменному члену так называемой главной серии, связанной с переходами из состояний 𝑃 в первое состояние строки 𝑆. Состояния 𝐷 соответствуют переменному члену «размытой побочной серии», излучаемой, подобно резкой побочной серии, при переходах в первое состояние второй строки. Наконец, состояния 𝐵 соответствуют переменному члену так называемой бергмановской серии, связанной с переходами в первое состояние третьей строки. Способ взаимного расположения различных рядов послужит иллюстрацией более детальной теории, которой мы займёмся позднее. Уже упомянутый кажущийся произвол, связанный с применением комбинационного принципа, в данном случае заключается в том, что при обычных условиях возбуждения возникают не все линии, отвечающие всевозможным комбинациям термов спектра натрия, но только те, которые на схеме обозначены стрелками.