Интересные результаты были получены также для спектров элементов с более высокими атомными номерами, объяснение которых тем временем существенно продвинулось благодаря работам Зоммерфельда, который ввёл несколько квантовых чисел для описания электронных орбит. В результате с помощью принципа соответствия удалось окончательно выяснить своеобразные правила, управляющие капризным на первый взгляд появлением линий, следующих из комбинационного принципа. Можно сказать, что квантовая теория не только дала простое объяснение комбинационного принципа, но, кроме того, сделала очень много для прояснения той таинственности, которая долгое время царила в применениях этого принципа.
Та же точка зрения оказалась плодотворной при исследовании так называемых полосатых спектров. Эти спектры обусловлены не отдельными атомами, а молекулами. Большое количество линий в этих спектрах обусловлено сложностью движения, связанной с колебаниями атомных ядер по отношению друг к другу и с вращением молекулы как целого. Обсуждаемые постулаты впервые были применены к рассматриваемой проблеме Шварцшильдом. Однако наиболее важный вклад внёс Хейрлингер, многое выяснивший своими важными работами о строении и возникновении полосатых спектров. Его выводы тесно примыкают к обсуждавшейся в начале лекции теории Бьеррума о влиянии вращения молекул на инфракрасные линии поглощения в газах. Совершенно очевидно, что мы уже не имеем права считать, что вращение находит свое отражение в спектрах так, как этого требует классическая электродинамика, а должны принять, что компоненты линий обусловлены переходами между стационарными состояниями, которые отличаются видом вращательного движения. Однако тот факт, что в этом явлении сохраняются существенные черты, предусмотренные классической теорией, является типичным следствием закономерности, определяемой принципом соответствия.
Естественная система элементов
Представления о возникновении спектров, развитые выше, послужили основанием для теории строения атомов элементов, оказавшейся пригодной для выяснения в общих чертах свойств элементов, находящих свое выражение в периодической системе элементов. Эта теория опирается прежде всего на соображения об образовании атома путём последовательного присоединения и связывания электрона в поле ядра. Как мы видели, оптические спектры элементов доставляют нам сведения о протекании последней стадии этого процесса образования атомов.
Представление о характере этих данных, получаемое при более внимательном изучении их, можно составить из рис. 8, на котором схематически изображены орбиты в стационарных состояниях, соответствующих дуговому спектру калия. Кривые показывают формы орбит последнего связанного электрона в атоме калия в стационарных состояниях. Их можно рассматривать как ступени процесса, при котором 19-й электрон оказывается связанным вслед за 18-м электроном, который вместе со всеми предшествующими уже находится на нормальной орбите. Чтобы не усложнять схемы, мы не пытались каким-либо образом изобразить орбиты этих внутренних электронов, отметив только пунктирным кругом область, внутри которой они движутся. Вообще говоря, в атоме с несколькими электронами орбиты имеют очень сложный вид. Вследствие симметричной природы силового поля ядра движение каждого электрона может быть приближённо описано как плоское периодическое движение, на которое накладывается равномерное вращение в плоскости орбиты. Поэтому всякая электронная орбита будет в первом приближении дважды периодической и будет определяться двумя квантовыми числами, подобно стационарным состояниям атома водорода при учёте прецессии, возникающей за счёт изменения массы электрона со скоростью.
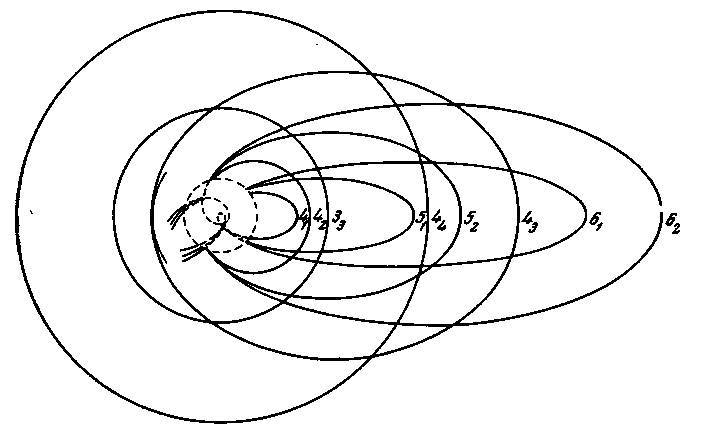
Рис. 8
Поэтому так же, как на рис. 5, электронные орбиты на рис. 8 обозначены символом 𝑛𝑘, где 𝑛 — главное квантовое число, а 𝑘 — вспомогательное квантовое число. В начальных стадиях процесса присоединения электрона, когда квантовые числа велики, орбита последнего связанного электрона проходит вне области ранее связанных электронов; на последних же стадиях дело обстоит иначе. Так, в атоме калия электронные орбиты со вспомогательными квантовыми числами, равными 2 и 1, проникают, как показано на схеме, во внутреннюю область. Вследствие этого орбиты будут чрезвычайно сильно отличаться от случая простого кеплеровского движения. Они будут состоять из ряда следующих друг за другом петель одинаковой величины и формы, каждая из которых повёрнута по отношению к предыдущей на значительный угол. На схеме изображена только одна такая внешняя петля. Каждая из них весьма напоминает часть кеплеровского эллипса. Они связаны, как изображено на схеме, внутренними петлями, имеющими сложный вид, на которых электрон весьма близко подходит к ядру. В частности, это относится к орбите со вспомогательным квантовым числом, равным единице, которая, как показывает подробное исследование, приближается к ядру ближе, чем орбита какого-либо из ранее связанных электронов.
Такое проникновение во внутреннюю область приводит к следующему. Несмотря на то, что бо́льшие части соответствующих электронных орбит расположены в силовом поле того же характера, что и поле ядра атома водорода, сила, с которой электрон удерживается атомом на данной орбите, значительно больше силы, удерживающей электрон в атоме водорода на орбите с тем же главным квантовым числом. В то же время максимальное расстояние электрона от ядра во время обращения значительно меньше, чем на подобной же орбите в атоме водорода. Как мы увидим, эта особенность связи электрона в атомах с большим числом электронов существенна для понимания своеобразной периодичности изменения свойств элементов с атомным номером, проявляющейся в периодической системе.
В прилагаемой таблице дана сводка результатов о строении атомов элементов. К этим результатам автор пришёл, рассматривая последовательное присоединение и связывание электронов полем атомного ядра. Числа, стоящие около символов элементов, означают атомные номера, которые указывают общее число электронов в нейтральном атоме. Числа в разных столбцах дают количество электронов на орбитах, соответствующих главным и вспомогательным квантовым числам, указанным сверху. Согласно общепринятой терминологии, мы будем называть для краткости орбиту с главным квантовым числом 𝑛 𝑛-квантовой орбитой. Электрон, связанный первым, движется по орбите, соответствующей нормальному состоянию атома водорода и обозначаемой символом 11. В атоме водорода имеется только один электрон. Мы должны предположить, что в атомах других элементов последующий электрон также будет связан на орбите того же типа 11. Следующие электроны, как видно из таблицы, будут связаны на двухквантовой орбите. Сначала они попадут на 21-орбиту, затем, однако, электроны оказываются связанными на 22-орбите до тех пор, пока первые 10 электронов не окажутся связанными, в результате чего будет достигнута законченная конфигурация двухквантовых орбит, которая, как мы полагаем, образована восемью орбитами, по четыре каждого типа. Нейтральный атом с такой конфигурацией мы встречаем впервые в неоне, завершающем второй период системы элементов. Последующие электроны связаны на трёхквантовых орбитах. После заполнения третьего периода, в элементах четвертого периода мы впервые находим электроны на четырёхквантовых орбитах и т. д.
Типы электронных орбит элементов
1
1
2
1
2
2
3
1
3
2
3
3
4
1
4
2
4
3
4
4
5
1
5
2
5
3
5
4