Случай временноподобного интервала. Событие 𝐻 расположено внутри светового конуса будущего с вершиной в событии 𝐺 в некоторой инерциальной системе отсчёта. Поэтому из 𝐺 в 𝐻 может попасть частица, движущаяся равномерно со скоростью, меньшей скорости света с точки зрения данной системы отсчёта. Но тот факт, что частица может непосредственно перейти из 𝐺 в 𝐻, никак не связан с конкретным выбором инерциальной системы. Поэтому событие 𝐺 предшествует событию 𝐻 в любой инерциальной системе, что и требовалось доказать.

Случай пространственноподобного интервала. Эта возможность исключается; интервал между двумя рассматриваемыми здесь событиями может быть лишь светоподобным или временноподобным, и не иначе. Поэтому теперь требуется доказать, что два события, разделённые пространственноподобным интервалом, не имеют универсального порядка во времени,— такой порядок во времени существует лишь для пар событий, интервалы между которыми являются светоподобными или временноподобными. Рассмотрим для примера в лабораторной системе отсчёта два события, разности координат которых равны 𝑥_𝐻-𝑥_𝐺=900 м и 𝑡_𝐻-𝑡_𝐺=540 м. Тогда пространственноподобный интервал между ними составляет

⎛

⎝

(

900

м

)

²

-

(

540

м

)

²

⎞½

⎠

=

720

м

Если рассматривать эти же события в системе отсчёта, быстро движущейся вправо, то они окажутся ближе друг к другу во времени, но величина интервала останется без изменения. В какой бы системе отсчёта ни проводились измерения, разности координат будут оставаться на гиперболе

(𝑥

_𝐻

-𝑥

_𝐺

)²

-

(𝑡

_𝐻

-𝑡

_𝐺

)²

=

(720

м

)²

(рис. 139). Когда новая система отсчёта достигнет достаточно большой скорости относительно лабораторной системы (такова, например, система 𝐽), то событие 𝐻 станет наблюдаться до события 𝐺. Такая ситуация имеет место для любой пары событий, разделённых пространственноподобным интервалом, и её можно описать с помощью гиперболы, подобной гиперболе на рис. 139. Короче говоря, если события 𝐺 и 𝐻 разделены пространственноподобным интервалом, то при выборе системы наблюдателя, движущейся достаточно быстро вправо или влево относительно лабораторной системы отсчёта, можно «сделать» событие 𝐺 сколь угодно более ранним или сколь угодно более поздним по сравнению с событием 𝐻.

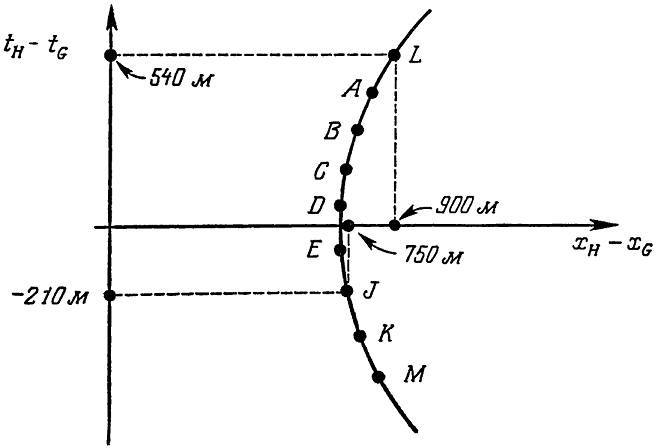
Рис. 139. Иллюстрация того, как выбор системы отсчёта сказывается на величине разностей пространственных и временных координат двух событий 𝐺 и 𝐻. Через 𝐿 обозначена лабораторная система отсчёта; система 𝐴 «медленно» движется вправо относительно лабораторной системы отсчёта; последовательность 𝐵, 𝐶, 𝐷, … изображает системы отсчёта, движущиеся со всё большими и большими скоростями вправо относительно лабораторной системы. Система 𝐽 такая, в которой разности координат вновь оказываются целочисленными. ▲

6. Расширяющаяся Вселенная

а) Средний чертёж на рис. 35 даёт для собственного времени, прошедшего между двумя вспышками, выражение

Δ

τ

=

√

(

Δ

𝑡)²-(

Δ

𝑥)²

=

√

(

Δ

𝑡)²-(β

Δ

𝑡)²

=

Δ

𝑡

√

1-β²

.

Из правого чертежа на том же рисунке следует выражение для времени, прошедшего между приёмом двух последовательных сигналов:

Δ

𝑡

_приём

=

Δ

𝑡

+

β

Δ

𝑡

=

Δ

𝑡

(1+β)

.

Исключим из первого уравнения Δ𝑡 с помощью второго и найдём скорость удаления осколков β:

β

=

(Δ𝑡_приём)²-(Δτ)²

(Δ𝑡_приём)²+(Δτ)²

.

Расстояние между осколком, на котором летит наблюдатель, и другим осколком бомбы, который он наблюдает, равняется времени, прошедшему с момента взрыва, умноженному на скорость удаления этих осколков друг от друга.

б) Пользуясь предыдущей формулой, определите скорость удаления звезды. Приравняйте Δτ собственному периоду световой волны, а Δ𝑡_приём — наблюдаемому периоду для света, приходящего от удалённого источника. Если Вселенная когда-то (𝑡=0) взорвалась, а её первоначальный объём был ничтожно мал, то теперь, в более поздний момент времени 𝑇, расстояние до каждой звезды (или галактики) будет равно β𝑇 (для вдвое быстрее удаляющейся галактики и расстояние будет вдвое большим). Расстояние же до галактики в тот более ранний момент, когда она испустила принятый нами теперь свет, было равно β𝑇/(1+β). Коэффициент красного смещения Δ𝑡_приём/Δτ превосходит 3 для самых быстро удаляющихся известных нам сейчас источников (так называемых квазаров — квазизвёздных объектов), однако расстояния до них неизвестны. В настоящее время мы умеем определять независимыми способами расстояния лишь для источников, удаляющихся от нас со скоростями β=0,2 и меньшими. Исходя из этих расстояний и наблюдаемого красного смещения, можно определить 𝑇 равным от 10¹⁰ до 1,4⋅10¹⁰ лет. ▲

7. Собственное время и связь

Ответ на первый вопрос: утверждение верно. На второй вопрос: нет, собственное время положительно. Одним из доказательств этого служит тот факт, что при отражении света вспышки между зеркалами на Луне можно добиться совпадения момента поглощения этого света с моментом прихода в эту точку частицы, испущенной с поверхности Солнца при вспышке. Собственное же время между событиями испускания и прихода к цели частицы с необходимостью больше нуля. Ответ на третий вопрос: нет, собственное время больше нуля. ▲

8. Время на сбор информации и на принятие решения

Время запаздывания равно 𝑅 м светового времени, так как для связи использовались непосредственно передаваемые световые сигналы. Все другие средства связи дают большие времена запаздывания. В распоряжении наблюдателя будет 3,4 сек для принятия защитных мер, т.е. на 0,4 сек больше, чем необходимые ему 3 сек. ▲

9. Лоренцево сокращение — подробный пример.

Решение дано в тексте.

10. Замедление хода часов

а) Можно, например, воспользоваться событиями, состоящими в пробивании отметок стрелкой часов на ракете в бумажных экранах, как это показано на рис. 38.

б) По определению Δ𝑥'=0. Подставляя эту величину в уравнение (42), получим (44).

в) Принцип относительности не нарушается ввиду симметрии между системами отсчёта. Отдельные покоящиеся в лаборатории часы отстают с точки зрения системы отсчёта ракеты, если их сравнивать последовательно со встречающимися им часами, покоящимися в системе ракеты [см. часть г)]. Нелишне также вспомнить анализ части г) в предыдущем упражнении.

г) По определению Δ𝑥=0. Подставляя эту величину в уравнение (39), получим (45). ▲

11. Относительная синхронизация часов

а), б) и в) При Δ𝑥=0 и Δ𝑡=0 формулы преобразования Лоренца дают Δ𝑡'=0 в системе отсчёта любой ракеты. Это верно вне зависимости от того, равны ли нулю Δ𝑦 и Δ𝑧 или не равны (вопрос б)). Если же Δ𝑡=0, а Δ𝑥≠0, тогда

Δ

𝑡'

=-

Δ

𝑥

sh

θ

_𝑟

≠

0

.

Уравнение (46) получается при использовании соответствующих условий (𝑡=0) в уравнениях (37).

г) Чтобы вывести (47), подставим 𝑡'=0 в уравнения (36).