Итак, масса покоя системы превосходит сумму масс покоя входящих в неё отдельных частиц на величину, равную полной кинетической энергии всех этих частиц (взятую в системе отсчёта, где полный импульс равен нулю!): 𝑀 =

𝑛

∑

𝑖=1 𝑚_𝑖 +

𝑛

∑

𝑖=1 𝑇_𝑖

❔

Обладает ли хоть каким-нибудь значением для эксперимента понятие «массы покоя физической системы»?

✔

Да. Масса покоя системы определяет её инертность, т.е. сопротивление ускорению, вызываемому силой, действующей на систему в целом. (Пример. Ящик с нагретым газом в принципе больше сопротивляется ускорению, чем этот же ящик, если газ в нем охладить). Масса покоя системы определяет также то гравитационное притяжение, с которым эта система действует на пробные частицы. (Пример 1. Горячая звезда, содержащая определённые количества атомов данных типов, в принципе сильнее притягивает свои планеты, чем такая же комбинация атомов, если их охладить. Пример 2. Облако электромагнитного излучения состоит из фотонов, масса покоя каждого из которых равна нулю, а «кинетическая энергия» положительна. Поэтому масса покоя облака излучения положительна. Облако оказывает гравитационное притяжение на удалённый объект, например Солнце, и в свою очередь подвержено гравитационному притяжению со стороны Солнца).

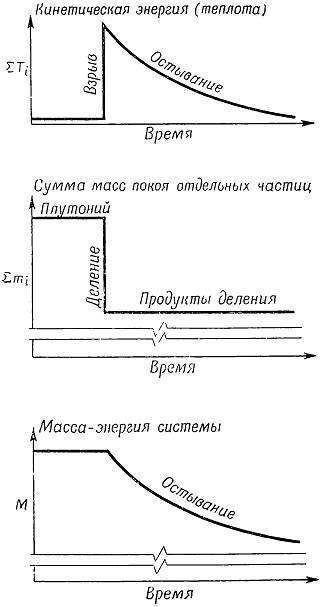
Рис. 95. Полная кинетическая энергия, сумма масс покоя отдельных частиц и масса покоя системы как функции времени, в течение которого взрывается ядерное устройство и остывают продукты взрыва.

❔

В космическом пространстве взрывается 20-мегатонная водородная бомба. Переводится ли при этом 0,93 кг массы в энергию?

[Δ𝑚= Δ𝐸/𝑐²= (20⋅10⁶ т)⋅(10⁶ г/т)⋅(10³ кал/г — эквивалент тринитротолуола)⋅(4,18 дж/кал)/𝑐²=(8,36⋅10¹⁶ дж)/(9⋅10¹⁶ м²/сек²)=0,93 кг]

✔

И да, и нет: необходима более корректная постановка вопроса. Масса покоя системы расширяющегося газа, осколков и излучения сохраняет ту же величину, какая была до взрыва,— масса покоя системы 𝑀 не изменяется. Однако произошло превращение водорода в гелий, а также произошли и другие ядерные превращения. В результате произошла «перекачка» величин между различными частями в формуле массы покоя системы: 𝑀 = ∑ 𝑚_𝑖 + ∑ 𝑇_𝑖

Первый член справа — сумма масс покоя отдельных составных частей системы — уменьшился на 0,93 кг.

⎛

⎝ ∑ 𝑚_𝑖

⎞

⎠

конечн =

⎛

⎝ ∑ 𝑚_𝑖

⎞

⎠

начальн -0,93 кг.

Второй член — сумма кинетических энергий, включая «кинетическую энергию» появившихся фотонов и нейтрино, — увеличился на столько же:

⎛

⎝ ∑ 𝑇_𝑖

⎞

⎠

конечн =

⎛

⎝ ∑ 𝑇_𝑖

⎞

⎠

начальн +0,93 кг. ⬆ первоначальное содержание тепловой

энергии в бомбе, практически равное нулю

по сравнению с 0,93 кг

Таким образом, часть массы покоя составных частей системы превратилась в энергию, но масса покоя системы в целом не изменилась

❔

Пусть ядерный взрыв будет произведён в подземной полости, а затем его продукты будут охлаждены, собраны и взвешены. Окажется ли тогда их масса меньше, чем масса первоначального ядерного устройства?

✔

Да. Решающим является здесь период ожидания, за который теплота и излучение успеют удалиться, так что продукты взрыва снова будут содержать такое же количество теплоты, какое было сначала в бомбе. Тогда в выражении для массы покоя системы 𝑀 = ∑ 𝑚_𝑖 + ∑ 𝑇_𝑖

второй член, величина которого резко возросла в момент взрыва, но понизилась за время охлаждения, в конечном итоге, после взрыва и последующего охлаждения, окажется прежним. Напротив, сумма масс покоя ∑𝑚_𝑖 всё время уменьшалась, а вместе с ней уменьшилась и величина массы 𝑀 того, что мы взвешиваем (после периода охлаждения); см. рис. 95

❔

Означает ли эйнштейновское утверждение об эквивалентности массы и энергии, что энергия — это то же самое, что масса?

✔

Нет. Величина энергии зависит от того, в какой инерциальной системе отсчёта мы рассматриваем частицу (или систему частиц). Величина же массы покоя не зависит от выбора инерциальной системы отсчёта. Энергия — всего лишь временная компонента 4-вектора, тогда как масса определяется как полная абсолютная величина этого 4-вектора (см. также упражнение 67). Временна'я компонента 4-вектора совпадает с его абсолютной величиной лишь в том частном случае, когда пространственные компоненты этого 4-вектора равны нулю, т.е. когда равен нулю импульс частицы (или полный импульс системы частиц). Лишь тогда величина энергии совпадает с величиной массы покоя

❔

Если говорить без всякого крючкотворства, является ли равенство 𝐸_обычн=𝑚𝑐² именно тем, что на самом деле существенно в законе эквивалентности массы и энергии?

✔

Исторически — да, в наше время — нет! В прежние времена не признавали, что и джоули и килограммы — это две единицы, различные лишь вследствие исторической случайности, но измеряющие одну и ту же величину — массу-энергию. Подобным же образом одну и ту же массу-энергию можно измерять и в других разных единицах — в эргах и в граммах. Множитель перехода 𝑐², подобно множителю перехода от секунд к метрам или от миль к футам, в наше время можно рассматривать, если угодно, как условность, но не как новую принципиальную величину

❔

Если основным во взаимосвязи массы и энергии является не множитель 𝑐², что же тогда будет там основным?

✔

Различие между массой и энергией в том, что масса характеризует абсолютную величину 4-вектора, а энергия — временную компоненту этого же 4-вектора. Все соображения, подчёркивающие это различие, идут на пользу пониманию взаимосвязи массы и энергии. Любая расплывчатость в терминологии, затушёвывающая это различие, является потенциальным источником ошибок и недоразумении

❔

Масса покоя 𝑀 системы свободно движущихся частиц определяется не как сумма масс покоя 𝑚_𝑖 отдельных частиц системы, но как сумма их энергий 𝐸_𝑖 (при этом—только в той системе отсчёта, где полный импульс системы равен нулю). Почему бы тогда не дать величинам 𝐸_𝑖 новое название, а именно не назвать их «релятивистскими массами» отдельных частиц? При таком обозначении (𝑚_𝑖)_релят = 𝐸_𝑖 =

⎧

⎪

⎪

⎨

⎪

⎪

⎩ = 𝑚_𝑖+𝑇_𝑖 , = √𝑚_𝑖²+𝑝_𝑖², =

𝑚_𝑖

√1-β_𝑖² ,

и можно записать 𝑀 =

𝑛

∑

𝑖=1 (𝑚_𝑖)_релят

✔

Понятие «релятивистской массы» (массы движения) приводит к недоразумениям, и мы его здесь не используем. 1) Оно применяет термин «масса», принадлежащий абсолютной величине 4-вектора, к совершенно другому понятию — временной компоненте 4-вектора. 2) При его использовании казалось бы, что увеличение энергии частицы при росте её скорости или импульса связано с какими-то изменениями во внутренней структуре этой частицы. На самом же деле увеличение энергии с ростом скорости заложено в геометрических свойствах самого пространства (преобразование Лоренца!)

❔

Может ли это различие между массой и энергией быть проиллюстрировано на какой-то простой диаграмме?

Рис. 96. 4-вектор энергии-импульса одной и той же частицы в трёх различных системах отсчёта.

✔

Да! На рис. 96. 4-вектор энергии-импульса одной и той же частицы изображён в разных системах отсчёта. Энергия в разных системах различна, но масса покоя (абсолютная величина 4-вектора) имеет во всех системах одно и то же значение 𝑚. (Кажущееся различие между значениями 𝑚 в трёх изображённых здесь системах вызвано тем, что мы пытались изобразить лоренцеву геометрию на эвклидовой плоскости. В лоренцевой геометрии квадрат гипотенузы равен разности квадратов катетов 𝐸' и 𝑝' или 𝐸ʺ и 𝑝ʺ)