а) Свет из точки 𝐸, приходящий в 𝑂 одновременно со светом из 𝐺, должен быть испущен из 𝐸 раньше, чем свет из 𝐺. Насколько раньше? Какой путь пройдёт куб за это время? Чему равно расстояние 𝑥 на рис. 73?
Рис. 73. Что видит наблюдатель, смотря снизу вверх.
б) Предположим, что некто решил истолковать видимую проекцию куба на рис. 73 как его поворот, а не лоренцево сокращение. Найдите выражение, описывающее угол такого кажущегося поворота φ не подвергнутого сокращению куба на рис. 74. Исследуйте это выражение в двух предельных случаях: β→0 и β→1.
Рис. 74. Как этот наблюдатель может истолковать свои визуальные наблюдения (проекцию рис. 73).
в) Соответствует ли выражение «на самом деле» реальному положению вещей в следующих высказываниях:
1) Наблюдатель в системе отсчёта ракеты говорит: «Мой куб на самом деле не подвергся ни повороту, ни сокращению».
2) Наблюдатель, пользующийся часовой сеткой лабораторной системы отсчёта, говорит: «Этот куб на самом деле подвергся лоренцеву сокращению, а не повороту».
3) Зритель, визуально проводящий наблюдения в лабораторной системе отсчёта, утверждает: «Куб на самом деле повернулся, а не претерпел лоренцево сокращение».
Как сформулировать в одной или двух фразах корректное высказывание, которое показало бы каждому из этих наблюдателей, что его партнёры должны были прийти к иным заключениям, чем он? ▼
51**. Парадокс часов. III
Можно ли улететь в место, удалённое на 7000 световых лет, и вернуться назад, постарев не более чем на 40 лет? «Да!»— к такому выводу пришёл инженер в правлении некой большой авиационной фирмы в своём последнем отчёте. Он рассмотрел путешественника, подвергающегося постоянному ускорению 1 𝑔 (или такому же торможению, в зависимости от этапа полёта; см. диаграмму пространства-времени на рис. 75). Верен ли его вывод при сделанных им предположениях? (Ради простоты, ограничьтесь анализом первого этапа путешествия, когда действует двигатель 𝐴, т.е. первыми десятью годами во времени астронавта, а затем удвойте пройденное при этом расстояние, чтобы узнать, какой путь проделан до самой дальней точки, достигнутой в путешествии).
Рис. 75. Мировая линия ракеты, движущейся по замкнутому пути с постоянным ускорением или торможением.
а) Ускорение не равно 𝑔=9,8 м/сек² относительно лабораторной системы отсчёта. Если бы оно было таким, то во сколько раз быстрее света двигался бы космический корабль к концу десятилетнего полёта? (1 год = 31,6⋅10⁶ сек). Если мы определяем ускорение не по отношению к лабораторной системе отсчёта, то по отношению к чему же мы его определяем? Обсуждение. Взглянем на медицинские весы, на которых стоит астронавт. Двигатели корабля пусть будут давать такую тягу, чтобы весы всё время показывали правильный вес. При этих условиях астронавт всё время подвергался ускорению 𝑔=9,8 м/сек² по отношению к такому космическому кораблю, который: 1) был бы мгновенно сопутствующим первому, так чтобы их скорости в этот момент совпадали, однако 2) не подвергался бы ускорению и поэтому 3) мог бы быть принят за инерциальную (мгновенную) систему отсчёта, ускорение относительно которой равняется 𝑔 (Начиная с этого места, мы переходим от 𝑔, выраженного в м/сек², к 𝑔*=𝑔/𝑐², выраженному в метрах пути за квадрат метров времени).
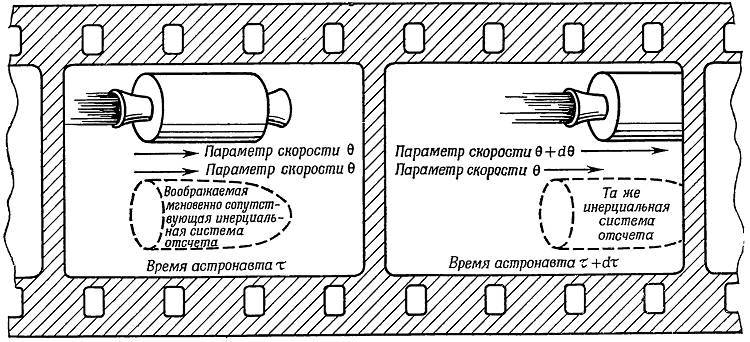
Рис. 76. Регистрация ускоренного движения ракеты в лабораторной системе отсчёта.
б) Какую скорость разовьёт космический корабль за данный промежуток времени? Но мы сразу же подвергнем этот вопрос критике и перефразируем его. Дело в том, что скорость β — недостаточно простая для исследования величина. Простым является параметр скорости θ, и его простота состоит в аддитивности. Смысл же аддитивности в том, что, если параметр скорости космического корабля на рис. 76 относительно воображаемой мгновенно сопутствующей инерциальной системы отсчёта меняется от 0 до 𝑑θ за время 𝑑τ по часам астронавта, то параметр скорости этого корабля по отношению к лабораторной системе отсчёта за тот же промежуток времени по часам астронавта изменится от своего первоначального значения θ до значения θ+𝑑θ. Свяжем теперь величину 𝑑θ с ускорением 𝑔* в мгновенно сопутствующей инерциальной системе отсчёта. В этой системе
𝑔*
𝑑τ
=
𝑑β
th 𝑑θ
≈
𝑑θ
,
так что
𝑑θ
=
𝑔*
𝑑τ
.
(64)
По прошествии каждого интервала времени 𝑑τ по часам астронавта происходит соответствующее увеличение параметра скорости космического корабля на 𝑑θ=𝑔*𝑑τ. Полная величина параметра скорости космического корабля в лабораторной системе отсчёта просто-напросто равна сумме всех этих последовательных увеличений параметра скорости. Пусть вначале космический корабль покоился. Тогда его параметр скорости линейно возрастал пропорционально величине истёкшего времени по часам астронавта согласно уравнению
θ
=
𝑔*τ
.
(65)
Так определяется параметр скорости θ космического корабля в лабораторной системе отсчёта в любой момент времени 𝑥 в системе отсчёта астронавта.
в) Какое расстояние в лабораторной системе отсчёта 𝑥 покрывает космический корабль за данный промежуток времени τ в системе отсчёта астронавта? В каждый момент скорость космического корабля в лабораторной системе отсчёта связана с его параметром скорости уравнением 𝑑𝑥/𝑑𝑡=th θ, так что расстояние 𝑑𝑥, пройденное за лабораторное время 𝑑𝑡 равно
𝑑𝑥=th θ 𝑑𝑡.
Вспомним, что соответствующие промежутки времени по часам астронавта 𝑑𝑥 представляются как более длинные промежутки 𝑑𝑡 в лабораторной системе отсчёта (замедление хода времени), и между ними существует связь
𝑑𝑡=ch θ 𝑑τ.
Отсюда расстояние в лабораторной системе отсчёта 𝑑𝑥, пройденное за время 𝑑τ по часам астронавта, равно
𝑑𝑥
=
th θ
ch θ
𝑑τ
=
sh θ
𝑑τ
.
Подставляя сюда выражение θ=𝑔*τ из пункта (б), найдём
𝑑𝑥
=
sh(𝑔*τ)
𝑑τ
.
Просуммируем (проинтегрируем) все эти малые перемещения 𝑑𝑥, начиная с момента «нуль» во времени астронавта и до конечного момента по этому времени; мы получим
𝑥
=
1
𝑔*
[ch(𝑔*τ)-1]
.
(66)
Так выражается расстояние 𝑥 в лабораторной системе отсчёта, покрытое космическим кораблём за любое данное время τ в системе отсчёта астронавта.
г) Переведём 𝑔* (в м/м²) в 𝑔=𝑔*𝑐² (в м/сек²) и τ (в м) в τсек=τ/𝑐 (в сек) в формуле (66). Выясним, был ли прав инженер, заключив в своём отчёте о возможности полёта, упомянутого в начале этого упражнения (1 год 31,6⋅10⁶ сек). ▼
52*. Наклонный стержень
Рис. 77а. Метровый стержень движется перпендикулярно самому себе (наблюдение в лабораторной системе отсчёта).