35*. Эксперимент Дикке ¹)

¹) См. R. Н. Diсkе, The Eotvos Experiment, Scientific American, 205, 84 (December 1961), а также P. G. Rоll, R. Кrоtkоv, R. H. Diсke, Annals of Physics, 26, 442 (1964). Первая из этих статей представляет собой популярный обзор, написанный ещё в начале проведения эксперимента. Вторая статья сообщает окончательные результаты эксперимента и тем более интересна, что в ней описаны те тонкие предосторожности, которые потребовалось предпринять для обеспечения исчерпывающего учёта всех привходящих влияний, могущих подействовать на течение опыта.

а) Высота пизанской «Падающей башни» составляет около 55 м. Галилей пишет: «Скорости падения в воздухе шаров из золота, свинца, меди, порфира и прочих тяжёлых веществ различаются настолько мало, что при падении с высоты 100 локтей (около 46 м) шар из золота наверняка не обгонит шара из меди более чем на 4 пальца. Проведя это наблюдение, я пришёл к выводу, что в среде, где исключено всякое сопротивление, все тела падали бы с одинаковой скоростью» ²). Приняв «4 пальца» равными 7 см, найдите наибольшее относительное различие ускорения силы тяжести Δ𝑔/𝑔 для шаров из золота и меди, соответствующее результатам опытов Галилея. Результат новейшего эксперимента Дикке: это отношение не превышает 3⋅10⁻¹¹. Приняв, что это отношение даётся таким новейшим результатом, вычислите, насколько разойдутся при своём падении с вершины 46-метровой вышки в вакууме одновременно брошенные два таких шара, когда первый из них достигнет поверхности Земли. С какой высоты при тех же условиях нужно было бы сбросить шары из разных веществ, чтобы при падении в вакууме в однородном гравитационном поле с напряжённостью 10 м/сек² они разошлись один от другого на расстояние в 1 мм? Сравните эту высоту с расстоянием между Землёй и Луной (3,8⋅10⁸ м), и вы увидите, почему эксперимент Дикке не мог состоять в сбрасывании шаров!

²) Галилео Галилей, Диалоги о двух новых науках. Соч., т. I, ГТТИ, М.— Л.„ 1934.

Рис. 50. Массивный шар, помещённый вблизи груза, вызывает статическое отклонение отвеса от вертикали.

б) Гиря отвеса массы 𝑚 подвешена на конце длинной нити, закреплённой на потолке герметически закрытой комнаты (рис. 50). Шар очень большой массы, помещённый сбоку от этой комнаты, действует на груз с силой гравитационного происхождения 𝑚𝑔_𝑠 направленной по горизонтали. Здесь 𝑔_𝑠=𝐺𝑀/𝑅², 𝑀 — масса шара, а 𝑅 — расстояние между грузом отвеса и центром шара. Эта горизонтальная сила вызывает статическое отклонение нити отвеса от вертикали на малый угол ε. (Аналогичный пример из практики: на севере Индии масса Гималайских гор приводит к небольшому отклонению линии отвеса, что затрудняет прецизионные геодезические промеры). Переместим теперь массивный шар так, чтобы он оказался у противоположной стены комнаты (рис. 51), и тогда статическое отклонение нити подвеса от вертикали, сохранив ту же величину угла, изменит своё направление на противоположное. Но ведь угол ε чрезвычайно мал (массив Гималаев вызывает отклонение нити подвеса всего на 5 дуговых секунд, т.е. на 0,0014°!). Однако, если всё время перемещать массивный шар вокруг герметически закрытой комнаты, наблюдатель в комнате сможет измерить обусловленное им гравитационное поле — для этого ему нужно со всё большей и большей степенью точности измерять полный угол, на который изменяется отклонение нити подвеса, 2ε=2 sin ε. Выведите уравнение, необходимое для вычисления величины 𝑔_𝑠 с помощью этого угла.

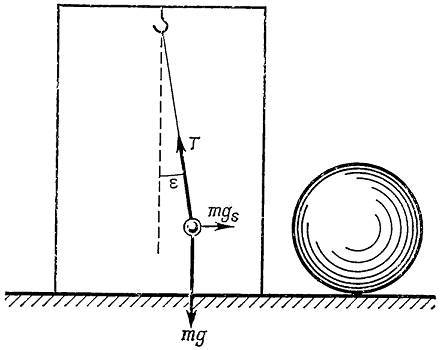
Рис. 51. Расположение шара по другую сторону отвеса приводит к статическому отклонению его от вертикали в противоположном направлении.

в) Мы, жители Земли, располагаем огромным шаром, эффективно совершающим ежедневный обход вокруг нас каждый день. Этот шар — самое массивное тело Солнечной системы — само Солнце! Чему равняется гравитационное ускорение 𝑔_𝑠=𝐺𝑀/𝑅², обусловленное Солнцем в окрестностях Земли? (Некоторые из постоянных, которые вам понадобятся при вычислении, можно найти в конце этой книги).

г) Необходимо учесть ещё одно ускорение, которое, однако, не будет фигурировать при окончательном сравнении величины гравитационного ускорения 𝑔_𝑠 для различных веществ. Таким дополнительным ускорением будет центробежное ускорение, вызванное движением Земли вокруг Солнца. Когда ваш автомобиль поворачивает, то вас прижимает к той его стороне, которая является внешней относительно направления поворота. Эта отбрасывающая сила, именуемая центробежной фиктивной силой или центробежной силой инерции, обусловлена ускорением вашей системы отсчёта (автомобиля) относительно центра дуги поворота. Величина этой центробежной силы инерции равна 𝑚𝑣²/𝑟, где 𝑣 — скорость движения автомобиля, а 𝑟 — радиус дуги поворота. Наша Земля движется вокруг Солнца по приблизительно круговой орбите. Сила гравитационного притяжения Солнца 𝑚𝑔_𝑠 действует на груз отвеса в направлении к Солнцу, центробежная же сила инерции 𝑚𝑣²/𝑅 стремится отбросить груз в сторону от Солнца. Сравните величину «центробежного ускорения» 𝑣²/𝑅 в окрестностях Земли с вычисленной вами в пункте (в) величиной гравитационного притяжения 𝑔_𝑠, имеющего противоположное направление. Чему равно результирующее ускорение (в направлении к Солнцу или от него), действующее на частицу, летящую вместе с Землёй, если его наблюдать в (ускоренно движущейся) системе отсчёта Земли?

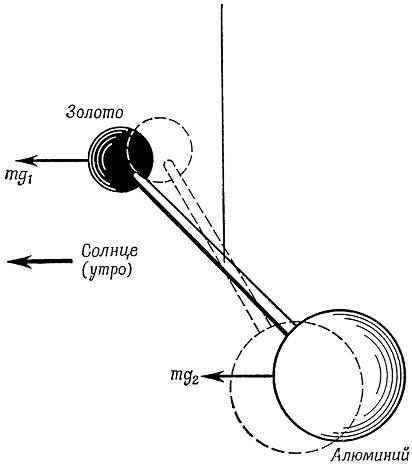
а) Предполагаемый эффект утром.

б) Предполагаемый эффект вечером.

Рис. 52. Схематическое изображение эксперимента Дикке.

Различие величин гравитационного ускорения золота и алюминия, вызванного Солнцем, привело бы к изменению знака результирующего закручивающего момента от утра к вечеру. Большой алюминиевый шар обладает такой же массой, как и маленький шар из золота, имеющего более высокую плотность.

д) Какова цель проведённого обсуждения? На груз отвеса, расположенный поблизости от поверхности Земли, действуют гравитационное ускорение 𝑔_𝑠 направленное к Солнцу, и равное ему по абсолютной величине, но противоположное по направлению центробежное ускорение 𝑣²/𝑅 (от Солнца). В результате в ускоренно движущейся системе отсчёта Земли действующая на груз результирующая сила, в целом обусловленная существованием Солнца, оказывается равной нулю. Но именно так мы и строили с самого начала инерциальную систему (разд. 2), положив, что эта система отсчёта находится в состоянии свободного падения к центру гравитационного притяжения. Покоящаяся на земной поверхности частица находится в состоянии свободного падения относительно Солнца, и поэтому результирующая сила, действующая на неё со стороны последнего, просто равна нулю. Какое же тогда может иметь отношение всё это к установлению равенства гравитационного ускорения, действующего на частицы различного состава, т.е. к предмету эксперимента Дикке? Ответ. Наша цель — обнаружить разницу (если таковая имеется) в гравитационном ускорении 𝑔_𝑠, действующем со стороны Солнца на различные вещества. Предполагается, что центробежное ускорение 𝑣²/𝑅 при движении вокруг Солнца по данной круговой орбите одно и то же для всех веществ и поэтому выйдет из игры при сравнении их ускорений. Рассмотрим крутильные весы, подвешенные за центр масс на кварцевой нити (рис. 52, а). На концах лёгкого стержня длины 𝑙 две равные массы из разных веществ (например, из алюминия и из золота). Предположим теперь, что величина гравитационного ускорения 𝑔₁, действующего на золото со стороны Солнца, несколько превышает ускорение 𝑔₂, действующее на алюминий со стороны Солнца. Тогда влияние Солнца выразится в форме слабого результирующего закручивающего момента, действующего на крутильные весы. Покажите, что в случае расположения Солнца, изображённого на рис. 52, а, этот закручивающий момент действует против часовой стрелки, если смотреть сверху. Покажите также, что его абсолютная величина даётся выражением