Таблица 7.

Классификация взаимной упорядоченности пар событий

Характер описания

Величина

квадрата интервала

Наименование

Временна'я часть интервала преобладает по сравнению с пространственной

Положительна

Временноподобный интервал

Временна'я часть интервала равна его пространственной части

Равна нулю

Светоподобный (изотропный) интервал

Пространственная часть интервала преобладает по сравнению с временно'й

Отрицательна

Пространственноподобный интервал

Три типа интервалов между парами событий: временноподобный, светоподобный и пространственноподобный

В зависимости от того, временноподобный он или пространственноподобный, интервал между двумя событиями обозначается по-разному. Временноподобный интервал записывается с помощью греческой буквы «тау» (τ) и называется также инвариантным временноподобным расстоянием или собственным временем (иногда — локальным временем) между двумя событиями:

Δ

τ

=

√

(

Δ

𝑡)²-

Δ

𝑥)²

.

(7)

Собственное время и собственное расстояние

Пространственноподобный интервал обозначается с помощью греческой буквы «сигма» (σ) и называется инвариантным пространственноподобным расстоянием или собственным расстоянием между двумя событиями:

Δ

σ

=

√

(

Δ

𝑥)²-

Δ

𝑡)²

.

(8)

Мировая линия частицы

Рис. 18. Временноподобная мировая линия частицы.

На рис. 18 изображено положение частицы в пространстве в функции времени в предположении, что частица в момент 𝑡=0 находилась в начале координат и затем двигалась вдоль оси 𝑥. Такой график зависимости положения в пространстве от времени на пространственно-временной диаграмме, называется мировой линией частицы. Каждые встречающиеся с частицей часы решётки регистрируют время встречи, так что мировая линия частицы в некотором смысле есть сумма таких отдельных событий-встреч. Никто никогда не наблюдал частиц, движущихся быстрее света. Поэтому любая частица всегда проходит за 1 м светового времени менее 1 м пути. Это значит, что разница во времени между всеми событиями на мировой линии частицы больше, чем расстояние между ними в пространстве, т.е. мировая линия частицы складывается из событий, временноподобных по отношению к исходному событию и по отношению друг к другу. Иначе говоря, мировая линия частицы должна быть временноподобной. Временноподобная мировая линия характеризуется в каждой точке 𝑃 касательной к ней в этой точке, лежащей где-то между мировыми линиями световых лучей, испущенных в той же точке. Эти световые лучи распространяются за 1 м светового времени на 1 м длины. События, лежащие на мировой линии светового луча, одинаково отстоят друг от друга в пространстве и во времени. Поэтому мировая линия светового луча складывается из событий, светоподобных по отношению к исходному событию и друг к другу. Иначе говоря, мировая линия светового луча должна быть светоподобной.

Путь в пространстве обладает длиной

Центральным в эвклидовой геометрии является понятие расстояния. Например, пользуясь гибкой измерительной рулеткой, легко найти расстояние Δ𝑠 вдоль пути, начинающегося на городской площади и идущего по кривой через городские ворота 𝐴 (рис. 19а). Расстояние Δ𝑠 между двумя любыми близкими точками на этом пути (например, теми, что обозначены на рисунке как 3 и 4) можно также вычислить исходя из разностей координат Δ𝑥 и Δ𝑦 этих точек в каждой из систем координат. Ввиду инвариантности расстояния оно будет для этой пары точек одним и тем же в любой из систем координат, хотя сами разности координат Δ𝑥 и Δ𝑦 будут различны в разных системах. Также и расстояния между всеми другими парами соседних точек на этом пути не будут зависеть от выбранной для расчётов системы координат. Значит, это заключение справедливо и в отношении суммы всех отрезков данного пути! Итак, разные землемеры, пользующиеся различными системами координат, найдут, что длина данного пути от определённой начальной точки 𝑂 до определённой конечной точки 𝐵 для всех них одинакова.

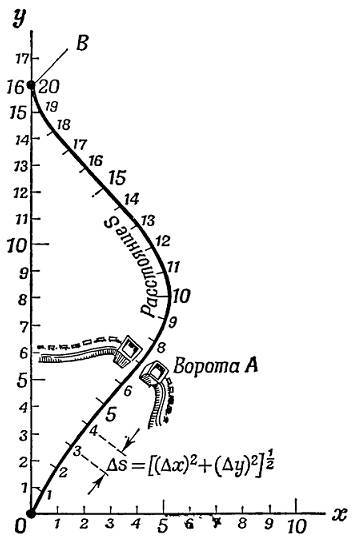
Рис. 19а. Расстояние вдоль искривлённого пути, начинающегося на городской площади. Заметим, что полное расстояние вдоль искривлённого пути от точки 𝑂 до точки 𝐵 больше, чем расстояние по прямому пути (ось 𝑦) от точки 𝑂 до точки 𝐵.

Рис. 19б. Собственное время вдоль искривлённой мировой линии на диаграмме пространства-времени. Заметим, что полное собственное время вдоль искривлённой мировой линии от события 𝑂 до события 𝐵 меньше, чем собственное время по прямой оси 𝑡 от события 𝑂 до события 𝐵.

Но от 𝑂 до 𝐵 можно пройти и по совершенно другому пути, например по прямой 𝑂𝐵 (рис. 19а). Этот новый путь, очевидно, обладает другой длиной, чем старый. Такое различие в длинах разных путей между 𝑂 и 𝐵 — настолько общеизвестный факт в эвклидовой геометрии, что не требует никаких комментариев и уж, конечно, не вызывает удивления. В эвклидовой геометрии путь по кривой между заданными двумя точками длиннее, чем прямолинейный путь между этими же двумя точками. Различие же длин для разных путей не приводит ни к каким противоречиям, и никто не станет заявлять, будто измерительная рулетка даёт неверный результат, если её протянуть в соответствии с кривизной пути.

Прямой путь обладает наименьшей длиной

Собственное время играет ту же роль для мировой линии в лоренцевой геометрии, какую играла длина для пути в эвклидовой геометрии. Пусть началом мировой линии служит событие 𝑂 а концом — событие 𝐵. Существует бесконечное множество разных мировых линий, соединяющих события 𝑂 и 𝐵. Соответствующий каждой из них промежуток собственного времени определён вполне однозначно, но различен для разных мировых линий. Удивительно ли это? Если да, то следует подробнее рассмотреть определение собственного времени и методику его измерения.

Протяжённость мировой линии измеряется собственным временем

Рассмотрим частицу, движущуюся от 𝑂 к 𝐵 по искривлённой мировой линии (рис. 19б) ¹). В этом случае частица движется реально вдоль оси 𝑥 с переменной скоростью. Пусть эта частица посылает световой сигнал через каждый метр времени по часам, движущимся вместе с частицей. Собственное время Δτ, прошедшее между каждыми двумя последовательными вспышками (например, обозначенными на рисунке через 3 и 4), можно вычислить, исходя из разностей координат Δ𝑥 и Δ𝑡 этих событий, измеренных в некоторой инерциальной системе отсчёта. Ввиду инвариантности этого интервала промежуток собственного времени между двумя данными событиями будет одним и тем же, в какой бы инерциальной системе отсчёта мы его ни вычисляли, хотя сами разности пространственных и временных координат Δ𝑥 и Δ𝑡 будут различны в разных системах отсчёта. Интервалы между всеми другими парами последовательных событий-вспышек на этой мировой линии не будут зависеть от выбранной для вычисления величины интервала системы отсчёта. Значит, это заключение справедливо и в отношении суммы интервалов собственного времени между всеми событиями-вспышками на данной мировой линии! Итак, разные наблюдатели в различных инерциальных системах отсчёта найдут, что промежуток собственного времени между определённым начальным событием 𝑂 и определённым конечным событием 𝐵 вдоль данной мировой линии для всех них одинаков.