Если нанести на карту еще больше магазинов, вы, вероятно, заметите, что часть из них находится на перекрестках, чуть в стороне от Юниверсити-авеню, а некоторые — вообще в других местах:

Тем не менее большинство магазинов все равно расположены довольно близко к центральной улице, и, если разрешено использовать для описания положения магазина только одно число, расстояние от вокзала вдоль этой улицы будет довольно удачным вариантом: пройдя этот отрезок и оглядевшись, вы с достаточной вероятностью найдете нужный магазин. Итак, вы только что понизили размерность «расположения магазинов в Пало-Альто» с двух измерений до одного.

У Робби, однако, нет преимуществ, которые дает человеку сильно развитая зрительная система, поэтому, если вы попросите его забрать белье из химчистки Elite Cleaners и учтете на его карте только одну координату, ему нужен будет алгоритм, чтобы «открыть» Юниверсити-авеню на основе GPS-координат магазинов. Ключ к решению проблемы — заметить, что, если поставить начало координат плоскости x, y в усредненное расположение магазинов и медленно поворачивать оси, магазины окажутся ближе всего к оси x при повороте примерно на 60 градусов, то есть когда ось совпадает с Юниверсити-авеню:

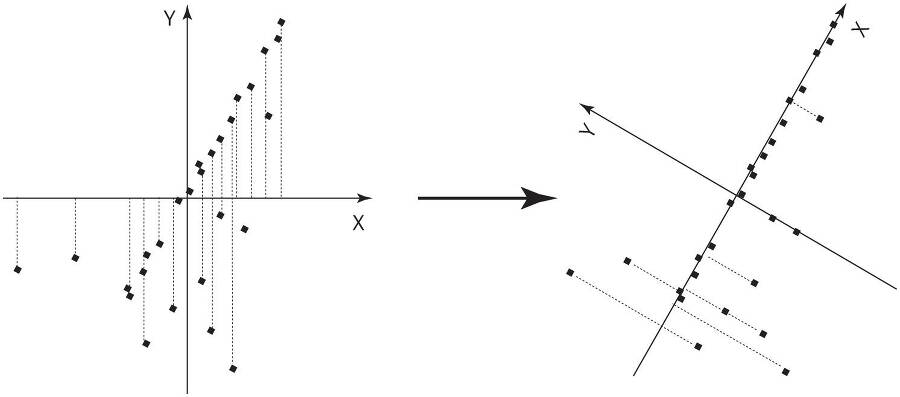
Это направление — так называемая первая главная компонента данных — будет направлением, вдоль которого разброс данных наибольший. (Обратите внимание: если спроецировать магазины на ось x, на правом рисунке они будут находиться дальше друг от друга, чем на левом.) Обнаружив первую главную компоненту, можно поискать вторую, которой в данном случае станет направление наибольшей дисперсии под прямым углом к Юниверсити-авеню. На карте остается только одно возможное направление (направление перекрестков). Но если бы Пало-Альто находился на склоне холма, одна или две главные компоненты частично были бы расположены непосредственно на холме, а третья — последняя — оказалась бы направлена в воздух. Ту же идею можно применить к тысячам и миллионам измерений данных, как в случае изображений лиц: нужно последовательно искать направления наибольшей дисперсии, пока оставшаяся вариабельность не окажется наименьшей. Например, после поворота осей на рисунке выше координата y большинства магазинов будет равна нулю, поэтому среднее y окажется очень маленьким, и, если его вообще проигнорировать, потеря информации получится незначительной. А если мы все же решим сохранить y, то z (направленная вверх) наверняка будет несущественна. Как оказалось, линейная алгебра позволяет провести процесс поиска главных компонент всего за один цикл, но еще лучше то, что даже в данных с очень большим количеством измерений значительную часть дисперсии зачастую дают всего несколько измерений. Если это не так, все равно визуальный поиск двух-трех важнейших измерений часто оказывается очень успешным, потому что наша зрительная система дает удивительные возможности восприятия.

Метод главных компонент (Principal Component Analysis, PCA), как называют этот процесс, — один из важнейших инструментов в арсенале ученого. Можно сказать, что для обучения без учителя это то же самое, что линейная регрессия для контролируемого множества. Знаменитая «клюшкообразная» кривая глобального потепления, например, была получена в результате нахождения главной компоненты различных рядов данных, связанных с температурой (годичные кольца деревьев, ледяные керны и так далее), и допущения, что это запись температуры как таковой. Биологи используют метод главных компонент, чтобы свести уровни экспрессии тысяч различных генов в несколько путей. Психологи обнаружили, что личность можно выразить пятью факторами — это экстраверсия, доброжелательность, добросовестность, нейротизм и открытость опыту, — которые оценивают по твитам и постам в блогах. (У шимпанзе, предположительно, есть еще одно измерение — реактивность, — но их с помощью Twitter не оценишь.) Применение метода главных компонент к голосам на выборах в Конгресс и данным избирателей показывает, что, вопреки расхожему мнению, политика в основном не сводится к противостоянию либералов и консерваторов. Люди отличаются в двух основных измерениях — экономических и социальных вопросах, — и, если спроецировать их на одну ось, либертарианцы смешаются с популистами, хотя их позиции полярно противоположны, и возникнет иллюзия, что в центре много умеренных. Попытка апеллировать к ним вряд ли окажется выигрышной стратегией. С другой стороны, если либералы и либертарианцы преодолеют взаимную неприязнь, они могут стать союзниками в социальных вопросах, где и те и другие выступают за свободу личности.

Когда Робби подрастет, он сможет применять один из вариантов метода главных компонент для решения проблемы «эффекта вечеринки», то есть чтобы выделить из шума толпы отдельные голоса. Схожий метод может помочь ему научиться читать. Если каждое слово — измерение, тогда текст — точка в пространстве слов, и главные направления этого пространства окажутся элементами значения. Например, «президент Обама» и «Белый дом» в пространстве слов далеко отстоят друг от друга, но в пространстве значений близки, потому что обычно появляются в схожих контекстах. Хотите верьте, хотите нет, но такой тип анализа — все, что требуется и компьютерам, и людям для оценки сочинений на экзаменах SAT (стандартизованный тест для приема в высшие учебные заведения США). В Netflix используется похожая идея. Вместо того чтобы рекомендовать фильмы, которые понравились пользователям со схожими вкусами, система проецирует и пользователей, и фильмы в «пространство вкуса» с низкой размерностью и рекомендует картины, расположенные в этом пространстве рядом с вами. Это помогает найти фильмы, которые вы никогда не видели, но обязательно полюбите.

Тем не менее главные компоненты набора данных о лице вас, скорее всего, разочаруют. Вопреки ожиданиям, это будут, например, не черты лица и выражения, а скорее размытые до неузнаваемости лица призраков. Дело в том, что метод главных компонент — линейный алгоритм, поэтому главными компонентами могут быть только взвешенные пиксель за пикселем средние реальных лиц (их еще называют «собственные лица», потому что они собственные векторы центрированной ковариационной матрицы этих данных, но я отхожу от темы). Чтобы по-настоящему понять не только лица, но и большинство форм в мире, нам понадобится кое-что еще, а именно нелинейное понижение размерности.

Представьте, что вместо карты Пало-Альто у нас есть GPS-координаты важнейших городов всей Области залива Сан-Франциско:

Глядя на эту схему, можно, вероятно, сделать предположение, что города расположены на берегу залива и, если провести через них линию, положение каждого города можно определить всего одним числом: как далеко он находится от Сан-Франциско по этой линии. Но метод главных компонент такую кривую найти не может: он нарисует прямую линию через центр залива, где городов вообще нет, а это только затуманит, а не прояснит форму данных.

Теперь представьте на секунду, что мы собираемся создать Область залива с нуля. Бюджет позволяет построить единую дорогу, чтобы соединить все города, и нам решать, как она будет проложена. Естественно, мы проложим дорогу, ведущую из Сан-Франциско в Сан-Бруно, оттуда в Сан-Матео и так далее, вплоть до Окленда. Такая дорога будет довольно хорошим одномерным представлением Области залива, и ее можно найти простым алгоритмом: «построй дорогу между каждой парой близлежащих городов». Конечно, у нас получится целая сеть дорог, а не одна, проходящая рядом с каждым городом, но можно получить и одну дорогу, если сделать ее наилучшим приближением сети, в том смысле, что расстояния между городами по этой дороге будут как можно ближе расстоянию вдоль сети.