(x),J

^ν

(0)]⟩

₀

.

(15.3)

При выводе этой формулы использован закон сохранения энергии-импульса, благодаря которому слагаемые, отвечающие переставленным токам J, равны нулю. Удобно определить тензор Π^μν выражением

Π

^μν

(q)=

i

∫

d

⁴

x e

^iq⋅x

⟨ΤJ

^μ

(x)J

^ν

(0)⟩

⁰

.

(15.4 а)

где p₁+p₂=q; нетрудно убедиться в справедливости соотношения Δ^μν=2ImΠ^{μν 23)}: сечение e⁺e^- -аннигиляции в адроны связано с мнимой частью фотонного поляризационного оператора.

²³⁾ Простой, но несколько громоздкий способ убедиться в этом состоит в применении соотношений унитарности (2.8) и (2.9) к процессу рассеяния на нулевой угол e⁺e^-→e⁺e^- во втором порядке теории возмущений по константе электромагнитного взаимодействия.

Небольшие усложнения возникают из-за интерференции сильных и электромагнитных взаимодействий. Поскольку поляризационный оператор Π^μν вычисляется во втором порядке теории возмущений по константе электромагнитного взаимодействия e, необходимо учитывать перенормировку электрического заряда, описываемую двумя диаграммами рис. 10, б. Простейшее решение этого вопроса заключается в рассмотрении тесно связанной с наблюдаемыми характеристиками процесса мнимой части поляризационного оператора ImΠ^μν, для которой подобных усложнений не возникает.

Электромагнитные токи являются сохраняющимися, поэтому их аномальные размерности равны нулю. Если из выражения для поляризационного оператора Π^μν выделить тензорную структуру -q^μνq²+q^μq^ν :

Π

^μν

(q)=(-g

^μν

q

²

+q

^μ

q

^ν

)Π(q),

(15.4 б)

то в соответствии с общими положениями теории для мнимой части поляризационного оператора можно написать соотношение

ImΠ

_R

(q;m(ν),g(ν);ν)=ImΠ

_R

(νn;

m

(Q

²

),

g

(Q

²

);ν),

Q

²

=-q

²

=s, n

²

=1 .

(15.5)

Таким образом, надо вычислить лишь величину ImΠ_R(q;m(ν),g(ν);ν) и произвести в ней замены q=ν, m(ν)→m(Q²), q(ν)→q(Q²). В нулевом порядке теории возмущений возникает диаграмма рис. 10, в, из которой, пренебрегая массами кварков, приводящими к поправкам порядка m²/s , получаем

ImΠ

₍₀₎

^R

=

1

12Π

3

_nƒ

∑

^ƒ=1

Q

₂

^ƒ

.

(15.6)

Формула (15.6) подтверждает результат старой партонной модели [58, 120], в которой кварки считались свободными. Поэтому принято рассматривать отношение сечения аннигиляции в адроны σ_h к сечению процесса е⁺е^-→μ⁺μ^-, вычисленному в низшем порядке теории возмущений по электромагнитному взаимодействию:

R(s)=

σ

^h (s)

σ

₍₀₎

^{е+е-→μ+μ-} (s)

.

(15.7)

В нулевом порядке теории возмущений это отношение равно

R

₍₀₎

(s)=3

_nƒ

∑

^ƒ=1

Q

2

ƒ

.

(15.8)

Поправки следующего порядка представлены диаграммами рис. 10, г. С точностью до замены фотона глюоном и учета теоретико-группового множителя Σ_a,kt^a_ikt^a_kj=C_Fδ_ij эти диаграммы аналогичны соответствующим диаграммам квантовой электродинамики, вычисленным много лет назад в работе [180]. Воспользовавшись этим результатом, получаем [18, 278]

R

⁽¹⁾

(s)=3

_nƒ

∑

^ƒ=1

Q

₂

^ƒ

⎧

⎨

⎩

1+

α_s(Q²)

π

⎫

⎬

⎭

(15.9)

Поправки второго порядка вычислены в работах [67, 95]. В перенормировочной схеме MS во втором порядке теории возмущений

R

⁽²⁾

(s)

=

3

_nƒ

∑

^ƒ=1

Q

₂

^ƒ

⎧

⎨

⎩

1+

α_s(Q²)

π

+r

₂

⎧

⎪

⎩

α_s(Q²)

π

⎫²

⎪

⎭ 

⎫

⎬

⎭

,

r

₂

=

[

2

3

ζ(3)-

11

12

]

n

_ƒ

+

365

24

-11ζ(3)≃2.0-0.12n

_ƒ

(15.10)

Здесь ζ — дзета-функция Римана, а для константы сильных взаимодействий α_s следует использовать выражение второго порядка теории возмущений.

Необходимо рассмотреть еще вопрос о том, сколько ароматов кварков следует учитывать. Этот вопрос тесно связан с проблемой кварковых масс. Если масса кварка m_q удовлетворяет условию s≫m²_q , то возникают поправки типа O(m²_q/s). В пределе s→∞ они пренебрежимо малы по сравнению с поправками любого порядка по параметру α_s . Совершенно иная ситуация возникает, когда m²_q≫s и передаваемой энергии недостаточно для рождения дополнительных кварк-антикварковых пар. Этот вопрос будет подробно рассмотрен несколько ниже; здесь же мы примем эвристический рецепт, состоящий в том, что суммы по ароматам кварков следует распространять на ароматы только тех кварков, массы которых удовлетворяют условию m²_q≪s. При этом порог рождения нового аромата 4m²_q≈s , в окрестности которого могут возникать сложные эффекты, рассматриваться не будет. Можно показать, что в этой области теория возмущений КХД непосредственно не применима.

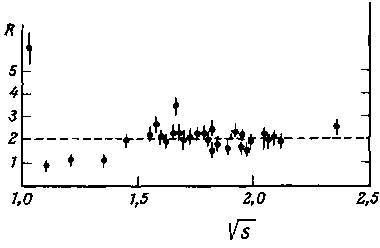
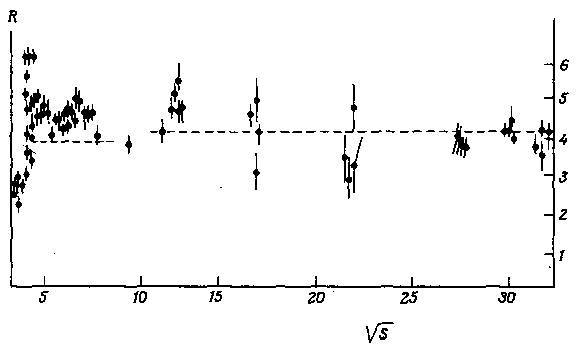
Рис. 11. Зависимость величины R от s. Штриховой линией показано (ведущее) предсказание КХД для R [265].

С учетом этих замечаний теоретические предсказания хорошо согласуются с экспериментальными данными, как видно на рис. 11, где приведены результаты первой экспериментальной проверки КХД²⁵. Однако из-за больших систематических ошибок экспериментальных данных при такой проверке трудно выйти за рамки ведущего порядка теории возмущений КХД.