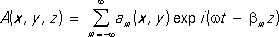
каждое слагаемое которого называется пространственной гармоникой. Здесь am — амплитуда пространственной гармоники, которая зависит от формы П. с.; (w — круговая частота электромагнитных колебаний; t — время; bm = b+ (2pm/d ) — волновое число m -той пространственной гармоники; i — мнимая единица. Основные характеристики П. с.: коэффициент замедления пространственных гармоник nт = bm•c /w, совпадающие по определению с коэффициентом преломления в оптике и численно равные отношениям фазовой скорости волны в свободном пространстве с к фазовым скоростям гармоник в П. с. w/bm ; групповая скорость dw/d bm , направление которой совпадает с направлением переноса энергии электромагнитных волн; дисперсия , характеризующая зависимость коэффициента замедления n от длины волны (в свободном пространстве (см. также Дисперсия света ). По значению коэффициент замедления определяют фазовую скорость волны, а по дисперсии можно судить о групповой скорости. Фазовые скорости и коэффициенты замедления пространственных гармоник различны, а их групповые скорости одинаковы.
В электронных приборах СВЧ, использующих П. с. в качестве замедляющих систем, скорость электронов обычно близка к фазовой скорости волны, а от групповой может отличаться не только по значению, но и по направлению. Совпадение направлений фазовой и групповой скоростей волны (положительная дисперсия) характерно для режима усиления колебаний, противоположные направления этих скоростей (отрицательная дисперсия) — для режима генерирования их.
Лит.: Айзенберг Г. 3., Антенны ультракоротких волн, М., 1957; Тараненко З. И., Трохименко Я. К., Замедляющие системы, К., 1965; Силин Р. А., Сазонов В. П., Замедляющие системы, [М.], 1966.
Р. А. Силин.
Рис. 1. Одномерно периодические структуры с различными типами дисперсионных характеристик: 1 — «широкая гребёнка» в волноводе с нормальной положительной дисперсией; 2 — диафрагмированный прямоугольный волновод с отрицательной дисперсией; 3 — «меандр» в волноводе с участками аномальной и нормальной положительной дисперсии; n — коэффициент замедления; l — длина волны.
Рис. 2. Двумерно (а) и трёхмерно (б) периодические структуры: d1 , d2 , d3 — периоды структур.
Периодическая функция
Периоди'ческая фу'нкция, функция, значение которой не изменяется при добавлении к аргументу определённого, неравного нулю числа, называемого периодом функции. Например, sin х и cos x: являются П. ф. с периодом 2p ; {x } — дробная часть числа х — П. ф. с периодом 1; показательная функция ex (если х — комплексное переменное) — П. ф. с периодом 2pi и т.п. Так как сумма и разность двух периодов есть снова период и, следовательно, любое кратное периода есть также период, то каждая П. ф. имеет бесконечное множество периодов. Если П. ф. имеет действительный период, непрерывна и отлична от постоянной, то для неё существует наименьший положительный период Т ; всякий другой действительный период той же функции будет иметь вид kT , где k = ±1, ± 2,.... Сумма, произведение и частное П. ф. с одним и тем же периодом являются П. ф. с тем же периодом. Производная П. ф. есть П. ф. с тем же периодом, однако интеграл от П. ф. f (x ) с периодом Т будет П. ф. (с тем же периодом) лишь в том случае, когда
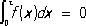
. Фундаментальная теорема теории П. ф. утверждает, что П. ф.
f (x) с периодом
Т [подчинённая ещё некоторым условиям, например непрерывная и имеющая в интервале (О,
T ) лишь конечное число максимумов и минимумов] может быть представлена суммой сходящегося тригонометрического ряда (ряда Фурье) вида:
;
коэффициенты этого ряда выражаются через f (x ) по формулам Эйлера — Фурье (см. Тригонометрические ряды , Фурье коэффициенты ).
Для непрерывной П. ф. комплексного переменного возможен случай, когда существуют два периода T1 и T2 , отношение которых не есть действительное число: если функция отлична от постоянной, то всякий её период будет иметь вид k1 T1 + k2 T2 , где k1 = 0,±1, ±2,... и k2 = 0, ±1, ± 2,.... В этом случае П. ф. называется двоякопериодической функцией . Рассматриваются ещё двоякопериодические функции второго и третьего родов; под ними понимают функции, которые при добавлении периодов к аргументу приобретают, соответственно, постоянный или показательный множитель [то есть f (x + T1 ) = a1 f (x ) и f (x + T2 ) = a2 f (x ) или f (x + T1 ) = и f (x + T2 ) -= ea2x f (x )].
Сумма П. ф. с разными периодами не будет периодической функцией в случае, когда периоды несоизмеримы [напр., cos х + cos
) не есть П. ф.]; однако функции такого рода обладают многими свойствами, приближающими их к П. ф.; такие функции являются простейшими примерами так называемых
почти периодических функций . П. ф. играют чрезвычайно большую роль в теории колебаний и вообще в математической физике.
Периодические возмущения
Периоди'ческие возмуще'ния в астрономии, см. в ст. Возмущения небесных тел .
Периодические психозы
Периоди'ческие психо'зы, повторно возникающие психические расстройства. Учение о П. п. зародилось в 40-х гг. 20в. и разрабатывалось преимущественно советскими психиатрами (Г. Е. Сухарева, Р. Я. Голант, А. З. Розенберг, Т. Б. Никонова и др.). Заболевания связывают с наследственным предрасположением, для реализации которого необходим внешний толчок — переутомление, инфекция, психическая или физическая травма. Согласно др. точке зрения, принятой в современной психиатрии, П. п.— вариант течения шизофрении или маниакально-депрессивного психоза . В клинической картине преобладают возбуждение, тревога, страх, возможны помрачения сознания, галлюцинации . Характерны острое начало и быстрое (через 2—3 нед , иногда через несколько сут ) выздоровление. П. п. хорошо поддаются лечению психотропными средствами . В межприступные периоды психика больных вполне сохранна.
Периодические решения
Периоди'ческие реше'ния уравнений, решения, описывающие правильно повторяющиеся процессы. Для теории колебаний, небесной механики и др. наук особый интерес представляют П. р. системы дифференциальных уравнений
,
i = 1,...,
n (1)
Это такие решения yi = ji (t ), которые состоят из периодических одного и того же периода функций независимого переменного t , то есть для всех значений t