Величина приливного ускорения a, которое испытывает человек на борту, прямо пропорциональна его расстоянию l от центра масс корабля.

Мы хотели разместить Драконоборец на высоте 406 километров от поверхности Яйца, так что корабль обращался вокруг звезды по синхронной орбите (с периодом, равным периоду ее собственного осевого вращения). Несмотря на то, что гравитационное притяжение в центре корабля компенсируется его орбитальным движением, при таком расстоянии от звезды приливное ускорение в расчете на один метр в 200 раз превышает земную силу тяжести в радиальном направлении к Яйцу Дракона и в 100 раз – по направлению внутрь в касательной плоскости звезды.

Для противодействия приливным силам экипаж Сент-Джорджа соорудил приливный компенсатор, состоящий из шести ультраплотных масс, образующих кольцевую формацию вокруг корабля. Как видно из рис. 7, в середине кольца приливная картина в точности противоположна той, что наблюдается над одной, изолированной массой. Подобрав массу m каждого из шести тел, а также радиус кольца r, нам удалось нейтрализовать приливные силы нейтронной звезды и подобраться к ней достаточно близко, чтобы собрать научные данные.

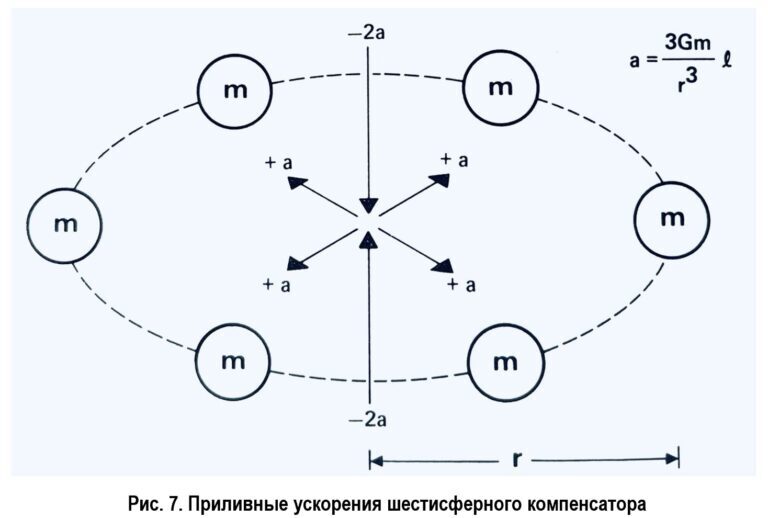
Впоследствии, когда чила решили сжать компенсаторное кольцо, приливы от каждой из шести масс стали мощнее приливов самого Яйца, так что последние пришлось «усилить», чтобы суммарная приливная сила оставалась примерно равной нулю. Для этого, как показано на рис. 8, чила воспользовались системой из двух добавочных масс. Такая конфигурация обеспечивает нулевую гравитацию в средней точке, поэтому орбитальные параметры тел, заключенных между добавочными массами, остаются неизменными, а ускорения в точках, удаленных от центра, возрастают точно так же, как и приливные ускорения над одиночной массой. Подробное описание приливных сил, а также способов их нейтрализации и увеличения при помощи конфигураций плотных сфер можно найти в одной старой статье, посвященной созданию локальной пикогравитации в окрестностях Земли [5].

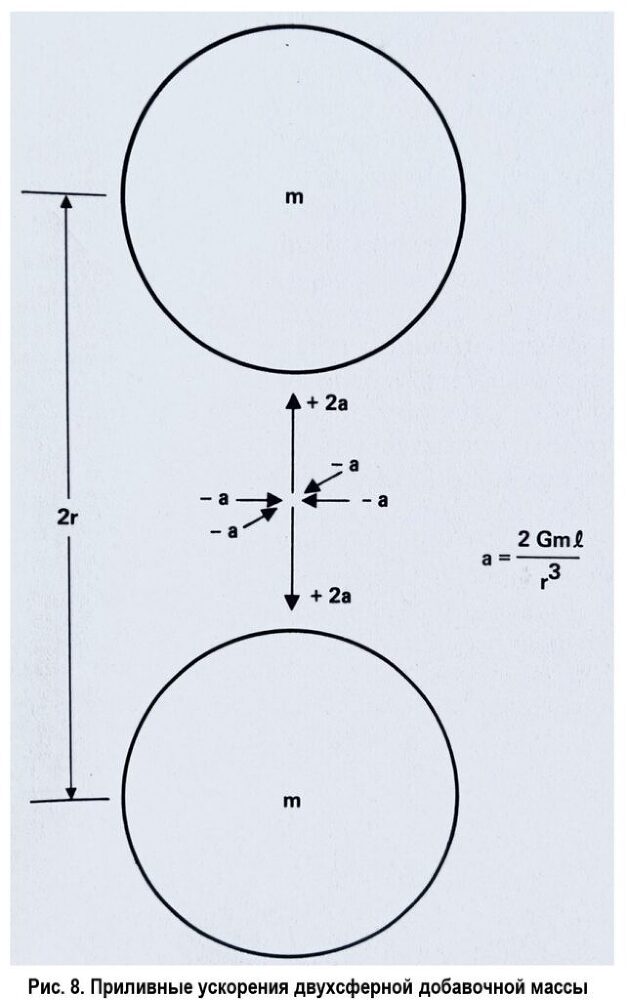
Приливные силы нейтронной звезды, а также необходимые для их сдерживания компенсаторы и добавочные массы не выходят за рамки представлений Ньютона, хотя он бы наверняка удивился тому, что в нашем мире могут существовать настолько плотные звезды и механизмы. У чила, впрочем, есть и более удивительные образчики ультраплотных машин. Мы знаем лишь, что технология, лежащая в основе таких машин, выходит за рамки эйнштейновой теории гравитации – особенно в области релятивистских скоростей, сверхвысоких плотностей и сверхмощных полей, доступных продвинутой цивилизации чила.

Секреты изготовления ультраплотных машин чила до сих зашифрованы их криптографическим кодом и хранятся на кристаллах голопамяти в Смитсоновском музее. Тем не менее, подобно тому, как ньютоновские законы гравитации остаются справедливыми для масс низкой плотности, законы гравитации Эйнштейна верны и для ультраплотных тел, а это, в свою очередь, дает нам некоторые подсказки насчет того, что может происходить в сверхплотных областях пространства, где эйнштейновы законы теряют свою применимость.

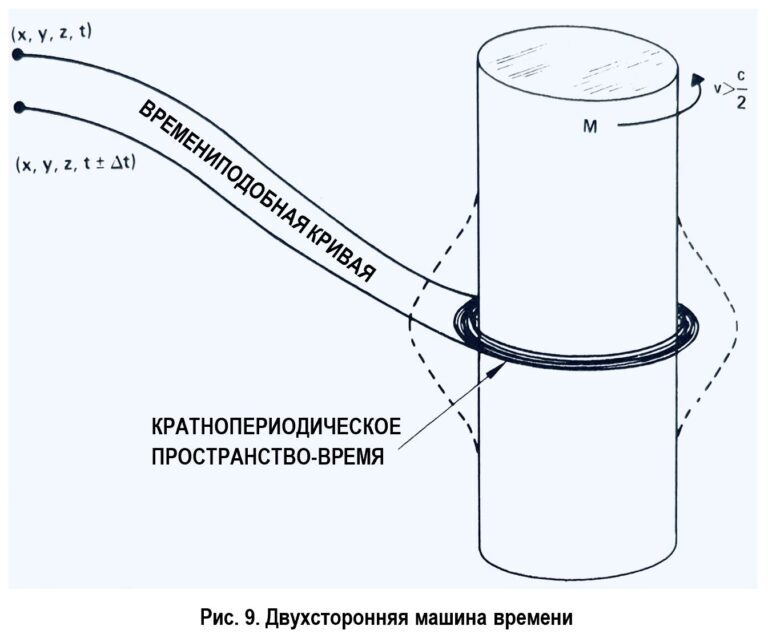
Чила также располагали машиной времени, которая позволяла им передавать сообщения в прошлое и будущее. Устройство такой машины – несмотря на парадоксы, которая она могла бы создать, если бы ее построили на самом деле – можно объяснить при помощи общей теории относительность Эйнштейна. Если длинный, ультраплотный цилиндр (см. рис. 9) неким образом раскрутить вокруг продольной оси, пока линейная скорость периферийных точек не превысит половину скорости света, то, как показывает несложный анализ [6], в районе его центра – но при этом за пределами самого цилиндра, – возникает область смешения пространства и времени. При подходящем выборе траектории объект или фотон можно заставить двигаться вокруг цилиндра – как в сторону его осевого вращения, так и против нее – в результате чего тот оказывается либо в прошлом, либо в будущем. Каким образом чила удалось изготовить вращающийся ультраплотный цилиндр и поддерживать его вытянутую форму достаточно долго для передачи сообщений, остается неясным.

«Рабочей лошадкой» первых космических полетов чила была гравитационная катапульта. Мы не знаем точного принципа ее работы, однако и здесь нам на помощь приходит общая теория относительности Эйнштейна. В ранних работах [7, 8] уже было показано, что эйнштейнова теория гравитации имеет ряд сходств с электромагнитной теорией Максвелла. В теории электромагнетизма основным источником всех сил является заряд электрона. Вокруг заряда существует электрическое поле. Если же привести заряд в движение, то образующийся ток породит поле магнитное. Мы также знаем, что электрическое поле возникает при росте или ослаблении магнитного – как результат его изменения.

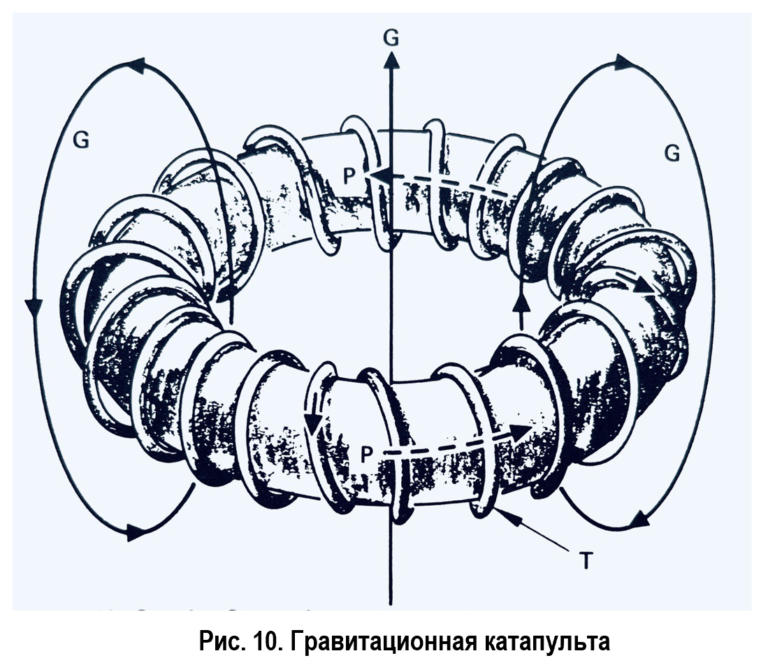
Аналогичными свойствами обладает и поле тяготения. Основным источником всех сил в данном случае выступает масса интересующих нас частиц. Эта масса создает вокруг себя гравитационное поле. При перемещении частиц возникает массовый ток, который, в свою очередь, порождает новое поле, представляющее собой гравитационный аналог магнитного. На рис. 10 показан тор, обмотанный трубкой с массовым током T и порождаемым гравитационным полем P, которое также называется протационным полем или полем Лензе-Тирринга. При увеличении или уменьшении протационного поля в центре катапульты возникает гравитационное поле G, которое будет толкать вверх любой объект, оказавшийся в центре кольца. Скорее всего, по аналогичному принципу работают и гравитационные катапульты чила, хотя в этом процессе, очевидно, используется и физика иного рода. Согласно предсказаниям теории Эйнштейна, машина, созданная на основе вещества нейтронной звезды, не сможет создать достаточно сильное гравитационное поле, чтобы запустить космический корабль с поверхности Яйца.

Самой удивительной из построенных чила ультраплотных машины стало миниатюрное искривление пространства. Некоторые подсказки, касающиеся его создания, мы опять-таки можем почерпнуть в ОТО, но не более того, ведь размер пространственной деформации оказался куда больше, чем следует из теории Эйнштейна. У полных уравнений Эйнштейна есть сравнительно простое точное решение, описывающее поле вокруг плотной вращающейся массы. Оно называется метрикой Керра.

Если предположить, что вращающаяся масса имеет форму ультраплотного кольца массой M и электрическим, либо магнитным зарядом Q (см. рис. 11), то с помощью метрики Керра можно показать [9, 10], что при достаточной плотности и скорости вращения кольца оно будет совмещать в себе свойства пространственной деформации и машины времени. Когда небольшое тело проходит сквозь горловину кольца, оно не выходит из машины с противоположной стороны!

Вместо этого, как следует из математических выкладок, тело попадает в гиперпространство, где время и пространство меняются местами. При движении согласно вращению кольца или против него тело будет перемещаться вперед или назад во времени. Чтобы вернуться в нашу Вселенную, объект нужно просто еще раз провести через горловину устройства. Такое быстровращающееся кольцо сверхвысокой плотности, очевидно, является неустойчивым, поэтому для спасения людей чила пришлось применить все достижения своих суперпродвинутых технологий, чтобы достаточно долго удерживать кольцо в стабильном состоянии.