6. Чтобы не впасть в ошибку, необходимо помнить, что формулы (1), (2), (3) имеют не просто математический смысл, вернее, не просто арифметический смысл. Надо помнить, что арифметика оперирует не с чистыми числами в полном смысле этого слова, но с количествами. Даже когда арифметика говорит об отвлеченных числах, все равно она их рассматривает главным образом с точки зрения их счетности, сосчитанности. Мы же, говоря о ц, б, м, имеем в виду как раз не абсолютные количества, но ту идею порядка, которая эти количества превращает в некие числовые, смысловые фигурности. Равенство (1) поэтому мы читаем так: тождество — везде в выражении одинаково присутствует, или: целое равно своей части. А равенство (2) так: различие везде одинаково присутствует в выражении, или: целое не равно своей части. Сравнивая эти два положения, мы можем поступить двояко — или говорить о различии тождественного, или о тождестве различного (что, конечно, есть одно и то же). Если мы говорим о различии тождественного, то, поскольку под тождеством мы понимаем не просто количественное тождество в абсолютном смысле, но именно тождественность повсеместного присутствия целого, тождественность отношения целого к части, — мы должны это отношение приравнять к отношению заведомо различествующих частей между собою. Если же мы будем говорить о тождестве различного, то, взявши отношение заведомо различных частей, мы должны то же самое отношение находить и во всех других частях. Чисто количественно формулу (3) нельзя понимать уже по одному тому, что и отношение

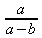
= (где α есть целое, а b — меньшая часть), взятое само по себе, чисто количественно, также не есть закон золотого деления, а последний предполагает выражение этой формулы, т. е. при–влечение материала, а не только чисто количественные операции.

Самым главным является во всем этом рассуждении то, что в законе золотого деления материальными средствами выражается смысл. В самом деле, как можно было бы материально, физически, т. е. в звуках и вообще величинах, выразить тождество отношения целого к части? Только так, чтобы физически же это отношение оставалось везде одинаковым, несмотря на различие величин. И вот мы видим, что при переходе от целого к одной части, меньшей, чем целое, образуется определенное отношение; при переходе от этой части к другой, меньшей, чем первая, полученное отношение (остается) тем же самым; при переходе к еще меньшей части — отношение опять то же и т. д. Это и значит, что мы физически и выразили самотождественное различие равновесно подвижного смысла. Итак, вот разгадка закона золотого деления. Это есть 1) единое, т. е. целостное, выражение 2) чистого смысла (или числа) 3) в аспекте подвижного покоя самотождественного различия. Только диалектически и можно разгадать этот универсальный и таинственный закон художественной формы, не прибегая ни к каким ни физическим, ни метафизическим теориям.

7. Можно из сферы смысла взять специально подвижной покой и выразить и его как таковой. Когда выражается подвижной покой смысла — возникает особое, совершенно специфическое строение музыкальной формы. Зададимся вопросом: как можно было бы выразить чисто смысловой подвижной покой чисто материальными, физическими, т. е. с точки зрения данного смысла совершенно алогическими, средствами? Какие физические элементы для этого оказываются необходимыми?

Чтобы решить этот вопрос, вспомним, что значит движение в музыке. Если я буду несколько раз подряд повторять один и тот же интервал, я буду тем самым стоять на месте и не двигаться. Чтобы двинуться с места, я должен, при наличии уже имеющегося музыкального элемента, напр. интервала, целой фразы и т. д. и т. д., дать нечто иное в сравнении с этим элементом; я должен нечто изменить в уже имеющемся музыкальном моменте. Движение в музыке имеет место тогда, когда наряду с элементом а есть еще элемент 6, не сходный с а, хотя и сравниваемый с ним, поскольку оба они движутся в одном и том же направлении. Проигравши одну какую–нибудь тему и тут же, непосредственно за ней, проигравши другую тему, я выражаю, насколько и как я музыкально движусь, я выражаю музыкальное движение. Но что теперь дает в музыкальном выражении смысловой покой? Как выражается смысловой покой в музыке? Физически его можно выразить только так, что мы как–то вернемся к исходному пункту, как бы описавши окружность. Если мы возьмем пространство, то подвижной покой в нем всецело выразится в виде круга. Сколько бы мы ни двигались по кругу и сколько бы раз ни проходили по его окружности, мы, в сущности, остаемся на том же самом месте и, вращаясь вокруг неподвижного центра, в своем движении остаемся в тех же самых границах, не выходим за пределы окружности. Этому пространственному подвижному покою соответствует в музыке, как мы сказали, возвращение того или иного музыкального элемента к исходной точке. Пусть мы имеем, напр., тему а. Чтобы быть в движении, она должна видоизмениться в тему b. Но чтобы в своем движении быть неподвижной, она должна снова прийти к теме а. То же самое должно относиться к количеству тактов, к ритмическим построениям и т. д. Все это я обозначаю общим именем «музыкального элемента». Итак, схема abba есть схема выражения чисто смыслового подвижного покоя, без специальной выраженности самотождественного различия. Особенный интерес это получает при той новой точке зрения на целое и элементы, к которой мы сейчас переходим.

До сих пор мы говорили о целом постольку, поскольку это надо было для суждения о переходе одного элемента целого к другому. Однако можно иметь в виду целое как такое в составе и совокупности всех его частей, не ограничиваясь специально рассмотрением перехода от одного элемента к другому. Тут получается та замечательная концепция музыкальной формы, которой в настоящее время может одинаково гордиться и диалектика, и эмпирическая наука о музыке. Рассмотрим участие всех основных категорий, конструирующих смысл, по порядку.

1. Смысл есть 1) различие, и музыкальная форма есть выражение этого различия. Выражая смысловое различие пространственными средствами, мы получаем по крайней мере две различные точки, т. е., другими словами, линию. Выражая смысловое различие музыкально–временными средствами, мы получаем, очевидно, по крайней мере два различных музыкальных элемента, напр. два звука, два интервала, два такта, две темы, две тональности и т. д.

2. Смысл есть 2) тождество, и музыкальная форма есть выражение этого тождества. Если бы мы захотели эту категорию выразить пространственно, мы должны были бы выразить то, что упомянутая выше линия, воплощающая категорию различия, тождественна себе самой. Как это сделать? Сделать это можно было бы только так, чтобы выбрать какую–нибудь третью точку и установить тождественное отношение нашей линии к этой третьей точке. Это значило бы, что мы опускаем на данную линию из третьей точки перпендикуляр. Другими словами, тождество и различие, самотождественное различие выражается в пространстве как координаты, и прежде всего как прямоугольные координаты. Самотождественное различие создает возможность внутри смысловой сферы отличать одно от другого и сравнивать одно с другим, т. е., попросту, ориентироваться в сфере смысла. То же самое делают координаты в пространстве. Что же теперь соответствует пространственным координатам в музыке? Как выражается самотождественное различие в музыке? Мы уже получили два разных элемента. Теперь надо показать, что они остаются самотождественными, т. е. отношение между ними всегда одно и то же, несмотря ни на какие изменения их самих. Выразить физически–музыкально это можно только так, что эти два элемента мы повторим в новой об–становке. Так, имея тему, мы можем дать вариации на эту тему. Это будет значить, что мы выразили в музыке самотождественное различие, так как вариация, во–первых, есть то же, что и заданная тема, а во–вторых, она, конечно, и нечто новое. Имея интервал в одном регистре, мы можем повторить его в другом регистре; имея музыкальную фразу (состоящую, стало быть, уже не из двух, а из большего числа элементов), занимающую определенное число тактов, мы можем повторить эту фразу в другой тональности, сохранивши ее мелодическую структуру и количество тактов и т. д. и т. д. Везде здесь будет выражаться самотождественное различие. Другими словами, самотождественное различие выражается в музыкально–временной форме при помощи принципа кратности отражения. Кратное от–ражение тех или других элементов создает в музыке ту самую систему ориентаций, которая в пространстве обнаруживается как система координат. Это — то, благодаря чему в музыке можно «одно» отделять от «другого» и «одно» сравнивать с «иным». Стоит вслушаться в любую пьесу, даже самую незначительную народную песню, чтобы сразу же заметить целую систему различных повторений и отражений. Без этого нет музыкального произведения и нет законченности его формы.