Выразить — значит соотнести с некоторым материалом, значит привлечь инородный материал, который сам по себе никакого отношения к данному смыслу не имеет, но отныне получает назначение носить на себе определенный, ему чуждый смысл. Так, желая «выразить» какое–нибудь раздумье и грусть в музыке, мы употребляем паузы, несмотря на то что пауза сама по себе, как пустой промежуток времени, никакого отношения к «раздумью» и ни к какому иному художественному осмыслению не имеет. Итак, мы должны выразить момент самотождественного различия в смысле. Посмотрим, что получится, если мы станем следить за выражением каждой из этих категорий в отдельности.
2. Мы выражаем тождество. Так как мы сейчас оперируем, как сказано, с материалом, который как таковой никакого отношения к смыслу и его тождественности не имеет, т. е. оперируем по существу с алогическим материалом, то тождество этими алогическими средствами мы можем выразить только так, что будем мыслить отношение целого ко всем своим частям совершенно одинаковым. Пусть ц обозначает целое, б — какую угодно большую часть, м — какую угодно меньшую часть. Если мы всерьез станем считать, что целое везде тождественно самому себе и, таким образом, одна часть абсолютно равна всякой другой части, всякая большая часть абсолютно тождественна всякой меньшей части, то мы можем написать следующее выражение:
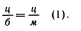
Это значит, что б = м что в ц нет никакой различенное. Так, если наиболее нравящаяся форма креста есть та, где вертикальная перекладина делится горизонтальной по закону золотого деления, т. е. вся она так относится к большей части, как большая к меньшей, то равенство (1) указывает на то, что между большей и меньшей частью вертикальной линии содержится в каком–то отношении абсолютное тождество. Именно, это отношение есть отношение к целому. Сразу видно, что это не есть тождество в абсолютном смысле, потому что одна часть остается тут сама по себе все–таки больше другой. Но все же тождество есть. И оно заключается в соотнесенности с целым. Большая и меньшая часть в каком–то смысле тождественно соотнесены с целой линией, т. е. одно и то же целое диктует свои законы большей и меньшей части. В чем конкретно содержится это тождество, пока не видно. Видно только то, что целое есть одна линия, одна и та же линия, и эта самотождественность одинаково присутствует в той или другой части, ибо то и другое суть и прямые линии и суть, кроме того, части общей вертикальной линии. Итак, равенство (1) мы можем прочитать так: тождество везде одинаково присутствует в выражении, или: отношение частей к целому везде в выражении самотождественно.
3. Но смысл есть не только самотождественность; он есть также и различие. И кроме того, это смысловое различие должно быть выражено, т. е. на алогическом материале должно быть показано, что все части целого отличны друг от друга. Как это сделать? Нас, следовательно, теперь интересует взаимоотношение частей. В равенстве (1) нас интересовало отношение частей к целому. Теперь нас интресует отношение не
и не
но отношение
. Что нужно о нем сказать? Тождество б и м достаточно выражено в равенстве (1). Как теперь выразить различие б и ж? Различие, как того требует диалектика, содержится везде ровно настолько же, насколько и тождество. Отношение
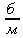
должно быть везде разным. Это значит, что отношение большего к меньшему мы должны уравнять с отношением чего–то такого к меньшему же, что является в данном случае универсальным. Только тогда мы выразим именно то, что эта разница большего и меньшего везде одинаково присутствует. Таким универсальным, конечно, может явиться только целое. Если отношение большего к меньшему действительно равняется отношению целого к меньшему, то это значит, что отношение целого ко всякой своей части везде совершенно различно. Чтобы получить меньшее, мы должны были хотя бы минимально отойти от целого, отличиться от него. И вот теперь оказывается, что, беря отношение любой большей части к любой меньшей, — мы находим, что оно равняется отношению целого к меньшему, т. е. оно всегда указывает хотя бы на минимальное раз–личие. Итак, большая часть всегда отлична от меньшей части, несмотря на общее тождественное отношение их обоих к целому. Поэтому равенство
=
(2) можно прочитать так: различие везде одинаково присутствует в выражении, или: отношение частей к целому везде в выражении различно. Тут также формально видно, в чем, собственно, проявляется различие. Если равенство (1) говорило о тождественном отношении частей к целому, то равенство (2) говорит о различном отношении частей к целому, т. е. имеются в виду, очевидно, их абсолютные величины.
4. Однако смысл есть не только тождество и не только различие, но самотождественное различие. Равенства (1) и (2) должны быть взяты как нечто целое. Самотождественность целого в своих частях должна быть абсолютно тождественной саморазличенности целого в своих частях. Самотождество и есть не что иное, как саморазличие. Это — нечто одно. Из сравнения формул (1) и (2) вытекает следующее отношение:
=
(3).
На первый взгляд это отношение и есть не что иное, как закон золотого деления, потому что он как раз и формулируется обычно в виде равенства отношения целого к большему с отношением большего к меньшему. Однако не надо соблазняться видимой точностью математической формулы. Мы занимаемся тут не математикой, но диалектикой, и отношения величин тут гораздо сложнее, чем в математике. Что мы получили в (3) ? Одно из двух: или это — выражение самотождественного различия целого с частями, и тогда это еще не есть закон золотого деления; или это — закон золотого деления, но тогда в этой формуле содержатся и еще некоторые моменты помимо момента самотождественного различия. Так как до сих пор мы говорили только о различии и тождестве, то будем пока отношение (3) читать так: отношение целого к своим частям везде тождественно и везде различно, или: отношение целого к частям есть самотождественное различие.
5. Вдумаемся теперь еще раз в закон золотого деле–ния и спросим себя: чего нам не хватает? Мы определили отношение большей части к целому и меньшей части к целому. Что нам еще надо? Нам нужен, несомненно, переход от целого к частям, и притом постепенный переход. До сих пор мы только сравнивали статически стоящие друг против друга целое и его части, устанавливая отношения тождества или различия. Но надо, чтобы мы прошли по пространству целого и зафиксировали бы этот переход в специальной формуле.
Не только одна пара категорий — различие и тождество — нашла свое выражение в законе золотого деления. Именно, раз мы переходим от ц к б, а от б к м, то тут мы невольно соблюдаем некую постепенность, некое движение. Переходя от б к м, а затем от ц опять все к тому же ж, мы, конечно, давали бы некую статическую формулу, в которой не было бы момента подлинного передвижения по пространству целого. Но именно формула (3) выражает и движение, а как такая, следовательно, и покой, ибо тут дается определенно положенное движение, дан переход и — остановка. Однако мы уже знаем, что эйдос есть единство не четырех, а пяти категорий, и потому эйдос золотого деления есть не что иное, как все та же единичность подвижного покоя самотождественного различия, данная как выражение алогических стихий времени, пространства или любой материальности. В тождестве и различии мы установили отношение между целым и частями и увидели, что это отношение, при всем различии частей, везде одинаковое; в движении и покое мы установили переход от целого к большей, от большей к меньшей, от меньшей еще к более малой части и т. д.; в подвижном покое самотождественного различия мы устанавливаем одинаковость отношения целого к части и частей между собою при всяких переходах по пространству целого, т. е. некое подвижное равновесие целого с частью; наконец, в единичности мы закрепляем определенную комбинацию частей и определенную фигуру их отношения между собою и к целому, ибо ведь переходить от целого к частям можно было на тысячу ладов. Отсюда подлинный феноменолого–диалектический смысл закона золотого деления и его разгадка заключается в том, что он есть принцип выражения смысла в аспекте его единичности подвижного покоя самотождественного различия. Диалектика закона золотого деления есть диалектика категорий тождества и различия, которые, будучи перенесены в сферу алогического материала (пространственных наличий, звуков) в своем подвижном равновесии, специфическим образом организуют этот материал, так что в результате всего этот материал должен своими слепыми материальными средствами воплотить и выразить целиком это подвижно–равновесное самотождественное различие. Таким образом, формула (3), если брать ее буквально, выражает не только тождество и различие, но и постепенность перехода.