Каждая эквипотенциальная поверхность имеет свою асимптотическую плоскость. Одна из эквипотенциальных поверхностей, показанная пунктиром, имеет коническую точку и лепесток, охватывающий точку 𝐴. Расположенные ниже эквипотенциальные поверхности однолистные и имеют углубление вблизи оси. Выше расположены эквипотенциальные поверхности, состоящие из замкнутой части, охватывающей точку 𝐴, и отдельного листа с небольшим углублением вблизи оси.

Если одну из поверхностей ниже точки 𝐴 принять за поверхность проводника, а за поверхность второго проводника, находящегося под другим потенциалом, принять другую эквипотенциальную поверхность, расположенную далеко внизу под точкой 𝐴, то система линий и поверхностей между этими двумя проводниками будет указывать распределение электрического поля. Если нижний проводник расположен очень далеко от точки 𝐴, то его поверхность очень близка к плоскости, так что мы имеем здесь решение для распределения электричества на двух поверхностях, которые обе почти плоские и параллельные друг другу, не считая выступа на верхней поверхности вблизи оси, величина которого зависит от того, какую эквипотенциальную поверхность мы выбираем.

121. На графике IV представлены эквипотенциальные поверхности и линии индукции для трёх точечных зарядов 𝐴, 𝐵 и 𝐶, причём заряд 𝐴 равен 15 единицам положительного электричества, заряд 𝐵 - 12 единицам отрицательного электричества и заряд 𝐶 - 20 единицам положительного электричества. Точечные заряды расположены на одной прямой, причём 𝐴𝐵=9, 𝐵𝐶=16, 𝐴𝐷=25.

В этом случае поверхность, на которой потенциал равен нулю, состоит из двух сфер с центрами в точках 𝐴 и 𝐶 и с радиусами, равными 15 и 20. Сферы эти пересекаются по окружности, которая проходит через плоскость рисунка в точках 𝐷 и 𝐷'; центром этой окружности является точка 𝐵, а радиус её равен 12. Эта окружность - пример линии равновесия, так как в каждой её точке равнодействующая сила равна нулю.

Если мы предположим, что сфера с центром в точке 𝐴 является проводником с зарядом в 3 единицы положительного электричества, находящимся под индуктивным воздействием 20 единиц положительного электричества в точке 𝐶, то этот случай будет представлен тем же графиком, если только убрать все линии внутри сферы 𝐴. Часть этой сферической поверхности, находящаяся под малой окружностью 𝐷𝐷', будет заряжена отрицательно из-за влияния заряда 𝐶. Вся остальная поверхность сферы будет заряжена положительно, а самая малая окружность 𝐷𝐷' будет линией нулевого заряда.

Этот же график можно считать представляющим сферу с центром в 𝐶, заряженную 8 единицами положительного электричества и находящуюся под воздействием 15 единиц положительного электричества, помещённого в точку 𝐴.

Можно также считать, что на графике представлен проводник, образуемый большими сегментами обеих сфер, смыкающимися в 𝐷𝐷', заряженными 23 единицами положительного электричества.

Мы ещё вернёмся к рассмотрению этого графика как иллюстрации к томсоновской Теории Электрических Изображений, см. п. 168.

122. Эти графики следует изучать как иллюстрации языка Фарадея, таких его выражений, как «силовые линии», «силы наэлектризованного тела» и т. д.

Слово Сила означает ограниченное выражение того действия между двумя материальными телами, благодаря которому их движение становится отличным от движения, которое было бы в отсутствие этого действия. Явление в целом при одновременном рассмотрении обоих тел называется Напряжением и может быть описано как передача количества движения от одного тела к другому. Если мы сосредоточиваем внимание на первом из двух тел, то напряжение, действующее на него, мы называем Движущей Силой или просто Силой, действующей на это тело. Она измеряется количеством движения, получаемым телом в единицу времени.

Механическое взаимодействие двух заряженных тел - это напряжение, а воздействие на одно из этих тел - сила. Сила, действующая на малое заряженное тело, пропорциональна его собственному заряду, а сила, приходящаяся на единицу заряда, называется Напряжённостью силы.

Слово Индукция употребляется Фарадеем для обозначения способа взаимосвязи зарядов наэлектризованных тел: каждая единица положительного заряда связана с единицей отрицательного заряда линией, направление которой в жидких диэлектриках совпадает в каждой точке с направлением электрической напряжённости. Такая линия часто называется Силовой лнией, но правильнее было бы называть её линией Индукции.

Далее, количество электричества в теле измеряется, согласно идеям Фарадея, числом силовых линий, или, лучше сказать, линий индукции, исходящих из тела. Все эти силовые линии должны где-то кончаться, либо на окружающих телах, либо на стенках и крыше помещения, либо на земле, либо на небесных телах, и, где бы они ни кончались, там присутствует количество электричества, в точности равное и противоположное по знаку тому количеству электричества, которое расположено на участке тела, из которого вышли силовые линии. Из приведённых графиков видно, что это действительно имеет место. Поэтому нет никакого противоречия между взглядами Фарадея и математическими результатами старой теории. Наоборот, идея силовых линий делает ясными эти результаты и даёт, по-видимому, средство перехода непрерывным образом от довольно косных понятий старой теории к представлениям, допускающим дальнейшее обобщение и создающим, таким образом, возможность расширения наших знаний в последующих исследованиях.

123. Графики на рис. 5 построены следующим образом. Возьмём сначала случай единственного силового центра - малого наэлектризованного тела с зарядом 𝑒. Потенциал на расстоянии 𝑟 равен 𝑉=𝑒/𝑟. Следовательно, положив 𝑟=𝑒/𝑉 мы найдём радиус 𝑟 сферы, на которой потенциал равен 𝑉. Придавая 𝑉 значения 1, 2, 3 и т. д. и построив соответствующие сферы, мы получим ряд эквипотенциальных поверхностей, на которых потенциалы измеряются натуральными числами. Сечение этих сфер плоскостью, проходящей через их общий центр, образует окружности, каждую из которых мы можем пометить числом, показывающим значение потенциала. Они показаны на рис. 5 справа в виде пунктирных полуокружностей.

Если имеется ещё другой силовой центр, мы можем тем же способом построить эквипотенциальные поверхности, относящиеся к нему, и если теперь задаться целью найти форму эквипотенциальных поверхностей, обусловленных обоими центрами, то следует лишь вспомнить, что если 𝑉₁ - потенциал, создаваемый одним центром, а 𝑉₂ - потенциал, создаваемый другим центром, то обусловленный обоими центрами потенциал равен 𝑉₁+𝑉₂=𝑉. Поскольку во всех точках пересечения эквипотенциальных поверхностей, относящихся к обоим семействам, мы знаем и 𝑉₁ и 𝑉₂ мы знаем также и значение 𝑉 в них. Поэтому, если построить поверхность, проходящую через все те точки пересечения, для которых 𝑉 имеет одно и то же значение, то эта поверхность совпадёт с истинной эквипотенциальной поверхностью во всех этих точках пересечения, и при достаточной густоте Построения исходной системы поверхностей можно построить новую поверхность с любой требуемой точностью. Эквипотенциальные поверхности, соответствующие Двум точечным зарядам, равным по величине, но противоположным по знаку, Показаны сплошными линиями справа на рис. 5.

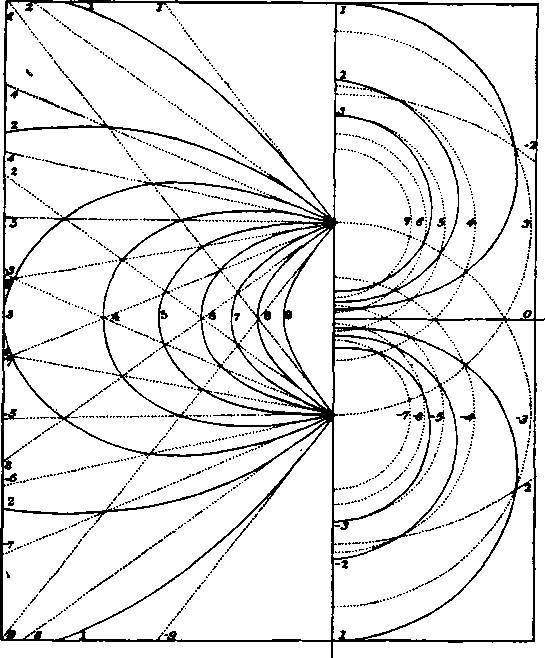
Рис. 5. Метод построения силовых линий и эквипотенциальных поверхностей

Этот метод может быть применён для построения произвольной системы эквипотенциальных поверхностей, если только потенциал является суммой двух потенциалов, для которых эквипотенциальные поверхности уже построены.

Силовые линии для одиночного силового центра представляют собой прямые, выходящие из этого центра. Если мы хотим указать этими линиями и интенсивность, и направление силы в любой точке, мы должны строить их так, чтобы они выделяли на эквипотенциальных поверхностях участки, по которым интеграл от индукции имеет определённое значение. Для этого лучше всего принять, что наша плоская фигура представляет собой сечение пространственной фигуры, образуемой вращением плоской фигуры вокруг оси, проходящей через центр сил. Любая прямая, выходящая из этого центра и образующая угол θ с осью, будет при этом описывать конус, и поверхностный интеграл от индукции по той части любой поверхности, которая вырезается этим конусом со стороны, прилегающей к положительному направлению оси, равен 2π𝑒(1-cos θ).