Математические подробности: другие меры риска
Те из вас, кто имеет серьезную математическую подготовку, осознают ограничения использования стандартного отклонения (SD, от standard deviation) как меры риска. Например, в реальном мире инвестиций доходности не следуют модели классического «нормального распределения», а гораздо ближе подходят к логарифмически-нормальному распределению. Далее, существует некоторая степень асимметричности относительно среднего значения (асимметрия), а также более высокая частота событий ближе к экстремумам диапазона (эксцесс). Наиболее значимый недостаток стандартного отклонения как меры риска в том, что одинаково важное значение придается доходностям выше и ниже среднего, в то время как только события, происходящие ниже среднего значения, важны при измерении риска инвестиций. Это навело некоторых ученых и практиков на мысль ввести полудисперсию, или среднее отклонение событий, происходящих ниже среднего значения, как более реалистичное измерение риска. Однако на практике как дисперсия, так и полудисперсия дают очень похожие результаты, и дисперсия / стандартное отклонение остается превосходной мерой риска. По сути, простая дисперсия / стандартное отклонение имеет дополнительное преимущество, дважды давая возможность поймать избыточную волатильность. В печально известном случае с компанией Long Term Capital Management она едва не оказалась на грани банкротства из-за того, что ей не удавалось достичь значительной отрицательной полудисперсии. Обычный расчет показателя стандартного отклонения / дисперсии ежемесячной доходности предупредил бы о надвигающихся проблемах за несколько лет.
Определений риска существует так же много, как и ученых в области финансов. В число возможных мер риска входят вероятность номинального убытка, или убытка с поправкой на инфляцию, «стандартное отклонение убытка», или вероятность получения более низкой доходности, чем по какому-либо индексу (например, S&P 500) или по казначейским векселям. Большинство отдает предпочтение мере, связанной с вероятностью того, что доходность инвестиций окажется ниже доходности безрискового актива, обычно казначейских векселей. Это легко рассчитать, используя кумулятивную функцию стандартного нормального распределения, подобную функции биноминального распределения, которую использовал наш воображаемый профессор статистики.
Вы можете придумать собственную меру риска. Такие индивидуальные меры риска и доходности называются функциями полезности.
Рис. 1.2. Распределение доходности актива «А»
В качестве более простого примера рассмотрим фонд, состоящий из акций латиноамериканских компаний, с ожидаемой доходностью в 15 % и очень высоким стандартным отклонением в 35 %. Это сигнализирует о вероятности убытка в 20 % или выше каждые шесть лет, убытка выше 55 % каждые 44 года и убытка выше 90 % каждые 740 лет. Очень сомневаюсь, что кто-либо из торговых агентов фонда или брокеров, продвигающих подобные фонды, в последние годы сообщал такую информацию своим клиентам. По сути, одним из характерных признаков сильно перекупленного рынка является общая недооценка рисков.
Если до сих пор вы понимали весь материал этой главы, то вы либо очень старались, либо хорошо оперируете числами (или прослушали курс статистики). Сегодня больше не читайте – отложите книгу, отдохните, займитесь другими делами. В следующий раз начнем с вами рассматривать реальные активы.
2. Риск и доходность
Отдельные классы активов: 1926–1998 гг.
К настоящему моменту у вас уже должно сложиться представление о статистическом значении доходности и риска. Вы готовы к анализу исторических данных за длительный период. Можно предположить, что вы не купите автомобиль или холодильник, не выяснив в специализированном издании, насколько надежно они работают и как часто их нужно ремонтировать. Аналогично вы не должны инвестировать значительную часть своего свободного дохода, не получив достаточного представления об ожидаемой доходности (надежности работы) и риске (информации о ремонте). К счастью, существует много полезных данных, которые относительно легко доступны и дешевы. Сколько времени нужно для того, чтобы получить четкое представление о долгосрочной доходности и риске класса активов? Мнения разойдутся, но для хорошего понимания ожидаемой доходности потребуются данные по меньшей мере за 20 или 30 лет. О риске актива можно получить хорошее представление из ежемесячных данных за период не более 5–10 лет.
Что касается американских ценных бумаг, то с этим никаких проблем: существуют полезные данные, восходящие ко времени образования Республики, по обыкновенным акциям и государственным облигациям и исключительно подробные данные начиная с 1926 г. Одной из выдающихся книг в мире инвестиций является монография Роджера Ибботсона Stocks, Bonds, Bills and Inflation, известная среди инвесторов как SBBI. В ней содержатся все возможные классификации доходности, рисков и корреляций по большому числу американских активов за период от месяца до десяти дней. Мы рассмотрим пять классов активов: акции крупных и мелких компаний США, а также 30-дневные, 5-летние и 20-летние казначейские ценные бумаги. В табл. 2.1 суммировано все, что вам действительно нужно знать об американских акциях и облигациях в целом; неплохо было бы запомнить примерные величины доходности и стандартных отклонений для этих активов.
Табл. 2.1. Доходность и стандартное отклонение по классам активов за период с 1926 по 1998 г.
Рассмотрим каждый класс активов отдельно. Необходимо обращаться к соответствующей серии графиков для каждого актива. В названиях правительственных ценных бумаг легко запутаться. Ценная бумага сроком менее 1 года называется казначейским векселем. Обязательство сроком от 1 до 10 лет называется казначейским билетом, а сроком более 10 лет – казначейской облигацией.
Казначейские векселя. Казначейские векселя – самый безопасный вид инвестиций. Динамика доходности казначейских векселей за период с 1926 по 1998 г. представлена на рис. 2.1. Если исключить банкротство государства, то по ним отсутствует вероятность дефолта, хотя Дядя Сэм под давлением инфляции время от времени печатает деньги. Цена этой безопасности очень высока: доходность составляет всего 3,77 %, что не намного выше темпов инфляции в 3,08 % за период с 1926 по 1998 г. Несмотря на то, что многие ученые считают казначейские векселя безрисковыми, беглый взгляд на график казначейских векселей позволяет увидеть значительную волатильность доходности, а это означает, что вы не можете полагаться на постоянный поток доходов. Этот риск надлежащим образом отражен в стандартном отклонении в 3,22 %. Но есть и положительная сторона: в конечном счете доходность казначейских векселей не отстает от темпов инфляции в долгосрочном периоде, хотя бывали длительные периоды, когда это наблюдение было неверным, особенно в 1970-е гг.
Рис. 2.1. Казначейские векселя, 1926–1998 гг.
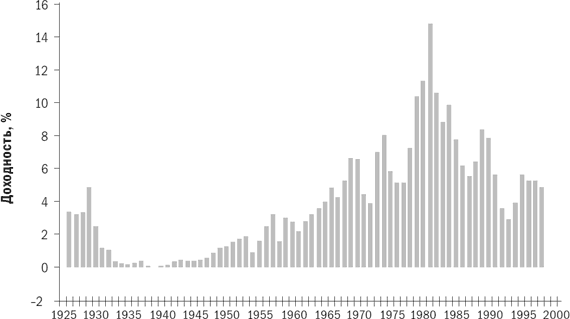
Среднесрочные (5-летние) казначейские билеты. Подобно казначейским векселям, среднесрочные (5-летние) казначейские билеты предлагают практически полную защиту от дефолта по основной сумме и процентам, но они связаны с одним риском – риском повышения процентных ставок. На рис. 2.2 изображен график доходности казначейских билетов за период с 1926– по 1998 г. Рыночная стоимость билета или облигации с фиксированным купонным доходом снизится при повышении процентных ставок, и чем больше срок погашения казначейского билета или облигации, тем больше будут потери. При сроке погашения в пять лет снижение рыночной стоимости основной суммы может превысить размер купона билета или облигации, что приведет к получению отрицательной общей доходности за год. Это случалось семь раз за период с 1926 по 1998 г., а самый большой убыток за этот период (2,65 %) получен в 1994 г. За несение этого риска в качестве вознаграждения вы дополнительно получите 1,5 % долгосрочной доходности. В итоге реальная (с поправкой на инфляцию) доходность составила около 2 %.