Данные отношения между категорическими суждениями были представлены в древнем квадрате противопоставлений[27]. Мы также можем построить следующую таблицу обоснованных выводов из каждого из четырех видов категорических суждений.

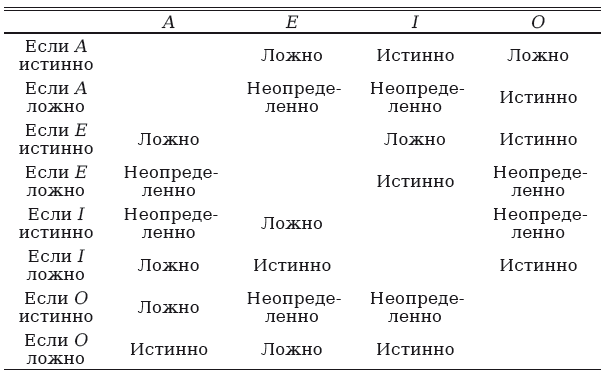
В заключение отметим, что без допущения относительно существования, которое мы сделали в начале этого параграфа, суждения типа I и О не могут быть выведены из суждений типа А и Е соответственно. Более того, без этого допущения суждения типа Л и Е не были бы противоположными, поскольку в таком случае могли бы вместе быть истинными. Так, суждения «все бессмертные люди находятся в этой комнате» и «ни один бессмертный человек не находится в этой комнате» были бы вместе истинными, если бы не существовало бессмертных людей. Однако поскольку ложно то, что существуют бессмертные люди, то (согласно интерпретации, которую мы дали частным суждениям) суждение «некоторые бессмертные люди находятся в этой комнате» и суждение «некоторые бессмертные люди не находятся в этой комнате» являются ложными. Следовательно, суждения, противоречащие данным, должны быть истинными.

Одним из источников интеллектуальных заблуждений является слишком поспешное допущение о том, что любые два неэквивалентных суждения являются взаимоисключающими. Люди долго спорили об отношении между сознанием и телом, между влияниями, оказываемыми наследственностью и окружающей средой, между эгоизмом и альтруизмом, искусством и природой. Зачастую эти споры проходили без осознания того, что из того факта, что рассматриваемые альтернативы не являлись эквивалентными, не следовало, что они исключали друг друга. Две вещи, соотносящиеся как часть и целое, не являются идентичными, однако они, разумеется, не являются противоположными. Суждение «все последователи православной греческой церкви – истинно верующие» не эквивалентно суждению «все христиане – истинно верующие», однако это не значит, что данные два суждения несовместимы.

Отношение противоречия мы видели в традиционном квадрате противопоставлений на примере таких суждений, как «все мусульмане – истинно верующие» и «некоторые мусульмане не являются истинно верующими». Однако неверно думать, что всегда легко распознать, какие суждения состоят в данном отношении друг к другу.

Предположим, что читатель, изучающий работу Руссо «Об общественном договоре», резко не согласен с первым предложением первой главы: «Человек рождается свободным, но повсюду он в оковах». Каким образом он может возразить данному утверждению? Или, допустим, он хочет отрицать утверждение, высказываемое несколько ниже в том же самом тексте: «Самый сильный никогда не бывает настолько силен, чтобы оставаться постоянно повелителем, если он не превращает своей силы в право, а повиновения ему – в обязанность». Какое суждение можно противопоставить данному в качестве противоречащего? Наконец, какое суждение, по мнению читателя, будет противоречить суждению «суверенитет… являет собою волю народа как целого либо – только одной его части»?[28]

Начнем с конъюнктивного суждения р: «человек рождается свободным и повсюду он в оковах». Утверждать данное суждение означает утверждать, что оба конъюнкта истинны, следовательно, отрицание данного суждения должно означать, что неверно, что оба конъюнкта истинны, т. е. что, по крайней мере, один из них ложен. В таком случае дизъюнкция q «некоторые люди не являются рожденными свободными или человек не является повсюду в оковах» будет противоречащим суждением относительно исходного. Читателю следует убедиться в том, что данные два суждения не могут вместе быть истинными и вместе быть ложными. Можно также получить и другие формы противоречия, поскольку данная дизъюнкция эквивалентна суждению «если все люди являются рожденными свободными, то они не суть в оковах», а также суждению «если человек повсюду в оковах, то некоторые люди не являются рожденными свободными».

Далее рассмотрим суждение «самый сильный никогда не бывает настолько силен, чтобы оставаться постоянно повелителем, если он не превращает своей силы в право, а повиновения ему – в обязанность». Это суждение является условным и может быть выражено следующим образом: «если самый сильный не превращает свою силу в право, а повиновение ему в обязанность, то он никогда не бывает настолько силен, чтобы оставаться постоянно повелителем». Данное суждение эквивалентно строгой дизъюнкции «неверно, что самый сильный не превращает свою силу в право, а повиновение ему в обязанность и что вместе с этим он является иногда достаточно сильным, чтобы оставаться постоянно повелителем». Суждением, противоречащим данному, следовательно, будет суждение «самый сильный не превращает свою силу в право, а повиновение ему в обязанность, и он иногда является достаточно сильным, чтобы оставаться постоянно повелителем».

Наконец, суждение «суверенитет являет собою волю народа как целого, либо только одной его части» является дизъюнктивным и может быть выражено как «суверенитет является волей народа как целого или он является волей одной его части». Поскольку данное суждение эквивалентно строго дизъюнктивному суждению, противоречить ему будет следующая конъюнкция: «суверенитет не является волей народа как целого и он не является волей одной его части».

Из сказанного следует, что суждение, противоречащее условному суждению, а также строгой или нестрогой дизъюнкции, всегда может быть выражено в форме конъюнкции.

С другой стороны, суждение, противоречащее конъюнкции, является либо условным, либо дизъюнктивным, либо строго дизъюнктивным суждением. Символьная запись выражает отношения между сложными суждениями в более компактном и точном виде. Поскольку

(р ⊃ q) ≡ (q′ ⊃ р′) ≡ (р′∨q) ≡ (p . q′)′,

суждение, противоречащее любому из приведенных, будет противоречить каждому из них. Следовательно,

(р ⊃ q)′ ≡ (q′ ⊃ р′)′ ≡ (р′∨q)′ ≡ (p . q′).

Иными словами, суждением, противоречащим суждению «если р, то q», будет «р и q′»; суждением, противоречащим суждению «р или q», будет «р′ и q′»; суждением, противоречащим суждению «неверно, что вместе р и q», будет «р и q».

Читателю следует обратить внимание на эквивалентность (р′ ∨ q)′ ≡ (р . q′). Данное отношение является абсолютно общим, и совершенно неважно, какие суждения мы подставим вместо символов. Поэтому подставим «r» вместо «р′». Тогда вместо «p» будет подставлен символ «r′». И тогда мы получим:

(r ∨ q)′ ≡ (r′. q′).

Данное отношение известно как теорема де Моргана. В ней утверждается, что отрицанием дизъюнкции (или суждением, противоречащим дизъюнкции) является конъюнкция, в которой конъюнкты противоречат соответствующим им дизъюнктам. В иной форме данная теорема выглядит следующим образом:

(р . r)′ ≡ (p′ ∨ r′).

Здесь утверждается, что отрицанием конъюнкции является дизъюнкция, в которой дизъюнкты противоречат соответствующим конъюнктам.

Мы удостоверились в том, что специально введенные символы существенным образом способствуют более ясному выражению логической структуры суждений, которая скрывается за громоздкостью обыденного языка. Вследствие этого читатель, несомненно, согласится с тем, что символы не препятствуют, а скорее способствуют пониманию. Обобщающая сила современной логики, равно как и современной математики, возможна во многом благодаря адекватности символической записи, принятой в этих дисциплинах.