В 1984 г. Экли, Хинтон и Сейновски предложили[1509] решение, в котором набор входных образов сопоставляется с набором выходных образов через небольшой набор скрытых нейронов. В последующем году появилась публикация[1510], посвящённая исследованию методов обучения такой сети.

Эта модель и получила название «машина Больцмана», в честь австрийского физика Людвига Больцмана, одного из основоположников статистической физики. Все синаптические связи между нейронами больцмановской машины — симметричные, а сами нейроны разделены на два множества — скрытые и видимые, где последние выполняют роль рецептивного слоя. Каждый нейрон может находиться в одном из двух состояний — «включённом» [on] и «выключенном» [off], причём это состояние он приобретает на основе некоторой функции вероятности от состояний нейронов, соединённых с нашим нейроном, и от синаптических весов этих связей. Синаптические веса являются действительными числами и могут принимать также и отрицательные значения. Довольно интересно здесь то, что авторы статьи не говорят о том, какая именно функция вероятности может быть использована в машине, что позволяет конструировать машины Больцмана на основе самых разных функций. Понятно, что классическим решением будет логистическая функция от суммы произведений состояний связанных нейронов (где «включённое» состояние соответствует 1, а «выключенное» — 0) на веса соответствующих связей. Каждый нейрон также имеет индивидуальную величину «смещения» [bias] (иногда также используется термин «порог» [threshold]), обозначаемую традиционно буквой θ. Смещение можно рассматривать как вес синапса, связывающего наш нейрон с особенным нейроном, находящимся в постоянно включённом состоянии.

Хинтон и его коллеги рассматривали машину Больцмана как модель для решения задачи «удовлетворения ограничений» [constraint satisfaction], то есть задачи поиска набора значений переменных, удовлетворяющих определённому набору ограничений.

В математической статистике модели, подобные машине Больцмана, называют марковскими случайными полями.

Впрочем, достижением Хинтона и его коллег стало не только и не столько создание прямого нейросетевого аналога случайных марковских полей и присвоение ему имени австрийского физика (тем более что некоторые исследователи склонны рассматривать машину Больцмана в качестве разновидности сети Хопфилда), сколько идея использования для обучения таких сетей так называемого алгоритма имитации отжига [simulated annealing].

Название этого алгоритма отсылает нас ВНЕЗАПНО к металлургии, в которой отжигом называется вид термической обработки стали, заключающийся в нагреве заготовки до определённой температуры, выдержке в течение некоторого времени и последующем, обычно медленном, охлаждении до комнатной температуры. Из школьного курса физики мы знаем, что температура вещества пропорциональна средней кинетической энергии составляющих его частиц. Чем выше температура, тем быстрее движутся частицы, по мере же остывания их движение становится всё более медленным, и в случае с кристаллическими телами частицы постепенно всё ближе и ближе перемещаются к позициям, соответствующим узлам кристаллической решётки. В процессе остывания система приближается к состоянию, соответствующему энергетическому минимуму. В машине Больцмана таким энергетическим минимумом является состояние, при котором набор синаптических весов (включая смещения) и состояний нейронов находится в «полностью непротиворечивом состоянии» (когда состояния нейронов видимого слоя, установленные в результате инициализации сети, совпадают с их состояниями, рассчитанными на основе синаптических входов). Энергию системы создатели модели описывают при помощи следующей нехитрой формулы:

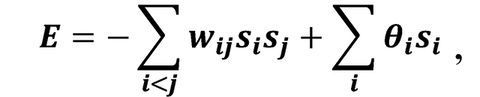
где w_ij — вес синапса, соединяющего нейроны i и j; s_i — состояние нейрона (0 или 1); θ — смещение. Условие i < j при суммировании нужно для того, чтобы исключить повторное суммирование для одних и тех же синапсов (поскольку синаптические связи в машине Больцмана полностью симметричны). Энергия суммируется для всего набора имеющихся у нас прецедентов. Процесс обучения начинается с точки, соответствующей случайному набору весов и некоторой величины температуры T. Затем на каждом шаге мы выбираем случайным образом новую точку в окрестностях текущей и рассчитываем величину энергии для неё. Если энергия в новой точке меньше, то мы переходим в неё со стопроцентной вероятностью. Если же величина энергии в новой точке больше или равна текущей, то мы переходим в неё или остаёмся в старой точке с некой вероятностью, зависящей от текущей температуры и энергии в старой и новой точках. Эта зависимость называется функцией вероятности принятия [acceptance probability function]. Можно использовать различные функции принятия, но классическая такова:

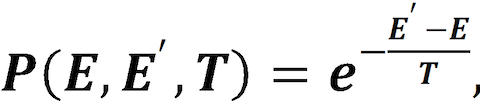
где P — вероятность перехода, E — энергия в текущей точке, E’ — энергия в новой точке, T — температура.

На следующем шаге мы уменьшаем величину T и повторяем процедуру, пока температура не достигнет нуля, а энергия — минимума.

Обученную машину Больцмана можно использовать так же, как и любой другой автокодировщик, — либо для расчёта латентного вектора для прецедента, либо для генерации нового прецедента на основе заданного (например, случайного) латентного вектора.

Ограниченная машина Больцмана, предложенная изначально в 1986 г. Полом Смоленским под названием Harmonium, представляет собой частный случай машины Больцмана, получаемый путём добавления следующего ограничения: синаптические связи могут связывать только скрытые нейроны с видимыми (но не скрытые со скрытыми или видимые с видимыми).

Завершённая в 1987 г. диссертация[1511] Лекуна, публикации[1512] Галлинари и его коллег, а также Бурлара и Кампа[1513] заложили основы применения автокодировщиков.

В 1990-е и начале 2000-х гг. исследования автокодировщиков продолжались. Например, в 1991 г. свет увидела работа[1514] Марка Крамера из MIT, в которой было показано преимущество автоэнкодеров (сам Крамер использовал термин «автоассоциативные нейронные сети» (Autoassociative Neural Networks)) над классическим методом главных компонент. В 1990-е и начале 2000-х гг. основным центром исследования автокодировщиков была группа Джеффри Хинтона в Торонто. В это время активно изучаются[1515]^, [1516] различные способы обучения таких сетей, позволяющие добиться наилучших результатов. Важным шагом вперёд становится появление глубоких сетей доверия — варианта ограниченной машины Больцмана с несколькими слоями скрытых нейронов (при этом допускаются связи между нейронами различных скрытых слоёв, но не внутри отдельного слоя). Для обучения таких сетей в начале 2000-х гг. в группе Хинтона применяли[1517] алгоритмы послойного обучения. Однако в целом можно сказать, что автокодировщики оставались в тени других нейросетевых моделей того времени (в первую очередь свёрточных и рекуррентных сетей). По всей видимости, в те годы многим исследователям казалось, что автокодировщики представляют главным образом теоретический интерес, а на практике могут применяться лишь в небольшом числе весьма специфических задач.