столбцом

оказывается естественной МО, строго локализованной на связи С-Н₁ и заселенной двумя электронами. Эту локализованную МО можно записать в виде следующей линейной комбинации базисных атомных орбиталей:

или

где

гибридная АО углерода, ориентированная вдоль связи С-Н₁, Существенно, что s-характер этой гибридной орбитали равен 33%, что соответствует sр²-гибридизации атома углерода и явно противоречит распространенному в химической литературе мнению о sp³-гибридизации углерода в метане и других насыщенных соединениях. Такое противоречие является следствием того что метод проектирования приводит к неортогональным наборам локализованных МО и гибридных АО, в то время как в теоретической химии обычно используется понятие об ортогональных орбиталях. Ортогонализация неортогонального набора четыоех эквивалентных гибридных АО h_iC по методу Лёвдина приводит в рассматриваемом случае (СН₄) к четырем ортогональным эквивалентным гибридным АО, которые идентичны гибридным АО углерода в метане, полученным из соображений симметрии. Вместе с тем следует отметить, что завышенный s-характер неортогональных гибридных АО углерода не является случайным. Как повышенная заселенность 2s-орбитали углерода в метане (1,2 против 1,0 для каждой из 2р-орбиталеЙ) он отражает "энергетическую предпочтительность" 2s-орбитали углерода по сравнению с его 2р-орбиталыо. В связи с этим уместно привести потенциалы ионизации свободного, т. е. химически не связанного, атома углерода, соответствующие его валентным орбиталям. Для 2s²2p²-конфигурации I_2s = 16,6 эВ и I_2p = 12 4 эВ; для 2s2p³-конфигурации I_2s = 24,7 эВ и I_2p = 12,4 эВ.

Существенно для понимания особенностей метода проектирования то, что в отличие от обсуждавшихся ранее методов этот метод не приводит к смешиванию МО σ- и π-типа локализованных на кратных связях, например, в молекулах N₂, CO, BF, C₂H₂ и C₄H₄. Однако вычисленные методом проецирования локализованные МО σ- и π-типа могут быть переведены дополнительным унитарным преобразованием в эквивалентные банановые МО аналогичные тем, которые были получены Эдмистоном и Рюденбергом (см. табл. 4.3).

Метод эталонной матрицы плотности. Метод эталонной матрицы плотности был предложен в 1968 г. Мак-Вини и Дель Ре [63] и получил дальнейшее развитие в работе [22].

Следуя Мак-Вини и Дель Ре, допустим, что МО могут быть локализованы в орбитали неподеленных и связывающих электронных пари, возможно, в вакантные орбитали некоторых атомов. Это означает, что каждую локализованную МО можно представить либо гибридной атомной орбиталью (ГАО), либо линейной комбинацией двух ГАО, относящихся к непосредственно связанной паре атомов. Будем предполагать пока, что заселенности этих гибридных АО равны, т. е. связи строго ковалентны. При учете поляризации двухцентровых локализованных связей орбитали неподеленных электронных пар и вакантные АО следовало бы рассматривать как случай предельной поляризации и выделять его особо не имело бы смысла. В силу сделанных допущений одноэлектронная матрица плотности в ортонормированном по методу Лёвдина многоцентровом базисе ГАО состоит из целых чисел 0, 1,2, причем каждой связывающей электронной пара соответствует блок

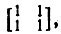
, неподеленной электронной паре — диагональный элемент 2 и остальные элементы матрицы плотности равны нулю. Такая идеализированная матрица плотности называется эталонной.

Коэффициенты гибридизации, образующие матрицу

(4.45)

где А, В, С, ...- атомы в молекуле и одновременно соответствующие им наборы АО, определялись Мак-Вини и Дель Ре из условия минимума суммы орбитальных энергий

(4.46)

b предположении, что матрица Фока F(P) фиксирована и не меняется при преобразовании U. Однако E_oрб составляет лишь часть полной электронной энергии E_эл, и то обстоятельство, что изменение δE_эл совпадает с δE_орб в линейном по δР приближении, не может служить обоснованием критерия Мак-Вини и Дель Ре, так как величина Е_эл должна быть стационарной относительно варьирования матрицы плотности, и определяюдими для ее изменения следует считать приближения более высокого порядка. В то же время вследствие зависимости F от матрицы плотности и, следовательно, от U точная минимизация Е_эл относительно U является довольно сложной задачей.

Более простым в вычислительном отношении является метод, основанный на минимизации (посредством гибридизации АО) :реднеквадратического отклонения заданной в гибридном базисе матрицы плотности P^h от эталонной

[22]. Для его реализации не требуется решения задачи самосогласованного поля при определении локализованных МО и соответствующих им ГАО, если эта задача уже решена в целях определения канонических МО или матрицы плотности. Основанием для такого выбора критерия оптимальности гибридных АО может служить то, что полная электронная энергия молекулы стационарна относительно малых вариаций одноэлектронной матрицы плотности

(4.47)

т.е.

(4.48)

при условии, что исходная матрица плотности Р вычислена в приближении самосогласованного поля и δР — достаточно малая (в смысле евклидовой нормы ||δP||) эрмитова матрица, определяемая формулой (4.47).

В качестве примера, иллюстрирующего формализм метода эталонной матрицы плотности, рассмотрим локализацию МО σ-типа в молекуле HCN. Предполагая, что в этой молекуле имеется одна неподеленная электронная пара, две остовные орбитали и две двухцентровые орбитали σ-типа, реализующие ковал ентные связи НС и CN, эталонную матрицу плотности записывают в виде

Исходная матрица плотности, вычисленная по методу МО, в ортонормированном базисе сферических АО

существенно отличается от

:

Однако преобразованием гибридизации АО базиса g:

(4.49)

и его ортогонализацией:

(4.50)

можно добиться того, что по отношению к новому базису

(4.51)

матрица плотности примет вид

В отличие от исходной матрицы Р матрица P^h может аппроксимироваться эталонной матрицей

. Последняя отвечает строгой локализации МО, которые в ортонормированном (по Лёвдину) базисе представлены столбцами матрицы