Приведенные выше рассуждения Хунда относились к случаю, когда расстояние между ядрами являлось достаточно малым, чтобы расщепление атомных термов было существенно меньше, чем расстояние между ними на шкале энергии. Если теперь несколько увеличить межъядерное расстояние и (одновременно) взаимодействие электронов считать несколько меньшим, то энергетическая последовательность электронных уровней будет определяться в первую очередь квантовыми числами n и l, во вторую очередь — квантовым числом |m| и только в третью очередь — квантовыми числами полного спина и абсолютной величиной проекции полного орбитального момента импульса на ось молекулы. Последовательность одноэлектронных состояний характеризуется тогда рядом

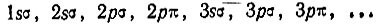
Обратимся теперь к рассмотренному Хундом случаю разделенных атомов. При достаточном разведении атомных ядер термы двухатомной молекулы должны перейти в атомные термы. Если заряды ядер одинаковы (гомонуклеарная молекула), то атомные орбитали могут порождать молекулярные орбитали согласно схеме:

Атомные 1s-уровни при сближении ядер расщепляются на два молекулярных одноэлектронных σ-уровня, один из которых соответствует молекулярной орбитали, симметричной относительной плоскости, равноотстоящей от ядер и перпендикулярной к оси молекулы. Этот уровень, согласно Хунду (а также Гайтлеру и Лондону), лежит ниже, чем второй σ_u-уровень, соответствующий антисимметричной орбитали.

При мысленном сведении ядер до их слияния симметричная молекулярная оуорбиталь переходит в 1s-орбиталь объединенного атома, антисимметричная — в 2р-орбиталь. Поэтому эти состояния Хунд обозначает символами 1sσ и 2рσ т. е. он рассматривает молекулу с точки зрения объединенного атома. Такой взгляд был впоследствии подвергнут критике Леннард-Джонсом и Герцбергом.

Для четырех первых электронов двухатомной молекулы при большом межъядерном расстоянии реализуется конфигурация (1sσ)²(2pσ)². Если затем добавить к ним пятый, то ему будет соответствовать 2s-орбиталь разъединенных атомов. Две таких орбитали, принадлежащие разным атомам, при сближении ядер преобразуются в симметричную и антисимметричную молекулярные σ-орбитали, причем энергия первой ниже, чем энергия второй, что следует из корреляции этих МО с орбиталями объединенного атома: симметричной МО соответствует 2sσ-AO, антисимметричной — 3pσ.

Таким образом, следует ожидать следующую последовательность одноэлектронных состояний двухатомной молекулы в порядке возрастания соответствующих им энергетических уровней: 1sσ, 2pσ, 2sσ, 3pσ, ...

Для первых восьми электронов при больших межъядерных расстояниях реализуется конфигурация (1sσ)²(2pσ)²(2sσ)²(3pσ)². Девятый электрон соответствует 2р-орбитали разъединенного атома. Шесть таких орбиталей (по три от каждого атома) преобразуются при сближении ядер в следующие МО: симметричную σ_g-МО, антисимметричную σ_u-МО и две двукратно вырожденные симметричные π_u-МО. Устанавливая соответствие между МО и АО объединенного атома, Хунд определил, что первая из названных выше МО является sσ (или dσ)-орбиталью, вторая- рσ-орбиталью, третья — pσ — и последняя dπ-орбиталями. При этом состояние 3sσ по энергии должно лежать ниже, чем 4рσ, а 2рπ ниже, чем 3dπ. По мнению Хунда, наиболее вероятной является следующая последовательность одноэлектронных состояний в порядке возрастания их энергии:

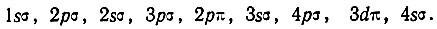
Таким образом, в 1927-1929 гг. Хундом были в качественном виде сформулированы некоторые важные идеи (одноэлектронного приближения, соответствия между атомными и молекулярными состояниями и т. п.), получившие затем более глубокую разработку. Однако его рассуждения о природе химической связи не являются специфическими для метода молекулярных орбиталей, а соответствуют более общему уровню рассмотрения, на котором не проявляются различия методов ВС и МО.

Другим исследователем, внесшим большой вклад в развитие молекулярно-орбитальной теории, был американский ученый Малликен. В 1925 г., изучая закономерности в молекулярных спектрах и сопоставляя их с атомными, он отметил сходство в спектральных характеристиках молекул CN, CO⁺, N₂⁺, ВО, BeF со спектром Na. Подобные аналоги были установлены в 1925-1927 гг. в работах Мекке, Бэрджа, Шпонер и других на примере молекул СО и N₂ и атома Mg, молекулы NO и атома Аl и т. п. Так, сопоставляя структуру молекулярных и атомных спектров, Бэрдж предположил, что энергетические уровни, связанные с валентными электронами молекулы, соответствуют "во всех существенных аспектах", т. е. по характеру вырождения, мультиплетности и взаимному расположению на энергетической шкале, уровням, на которых находятся валентные электроны в изоэлектронных, точнее изовалентноэлектронных, атомах. По предложению Бэрджа, молекулярные уровни стали обозначаться теми же буквами (s, p, d, f,... и т. п.), что и атомные, но только заглавными. Его обозначения ¹S, ¹Р, ^lD, ²S, ²Р соответствуют современным:

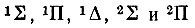
(с подуровнями ²∏¹_/2 и ²∏³_/2).

Указанные аналогии натолкнули Малликена на мысль, что каждому электрону в молекуле можно приписать определенную орбиту [64-65]. Например, электроны в молекулах CN и ВО должны характеризоваться квантовыми числами, аналогичными квантовым числам в атоме Na (хотя эти молекулы имеют на два K-электрона больше). Созданная Малликеном теория в значительной степени основана на изложенных выше идеях Хунда. Малликен отмечает, что интерполяция между случаями строгб разделенных атомов и объединенного атома, проводившаяся Хундом, оказывается полезной для оценки электронного состояния двухатомных молекул. В частности, модель объединенного атома позволяет использовать принцип Паули для определения максимально возможного числа электронов, соответствующих любым заданным квантовым числам. Квантовые числа, характеризующие электронное состояние молекулы, получаются из квантовых чисел, соответствующих электронному состоянию объединенного атома в предположении, что этот атом помещен в сильное электрическое поле. Наложение последнего эквивалентно мысленному расщеплению ядра объединенного атома на отдельные ядра, входящие в молекулу.

Однако реальная последовательность термов по энергии может отличаться (и весьма значительно!) от последовательности, имеющей место в сильном электрическом поле. Распределение электронов для основного состояния молекулы может соответствовать их распределению в некотором возбужденном состоянии объединенного атома, и наоборот.

Так как основная часть информации о прочности химических связей основана на спектроскопических данных, Малликен высказал предположение, что при анализе электронной структуры молекулы может оказаться полезным метод, аналогичный использованному Бором для определения электронной конфигурации атомов. Этот метод состоит в том, что все электроны мысленно удаляются из атома, а затем по одиночке возвращаются в атом, занимая доступные орбиты с наиболее низкой энергией. Конечно, применение этого метода к молекулам затруднялось тем, что отсутствовала достаточная информация об энергетической последовательности орбит в молекуле. Для решения этой проблемы были использованы корреляции между предельными случаями объединенного и изолированного атомов. Развитие метода Хунда Малликеном, по мнению последнего, "состояло прежде всего в попытке определить квантовые числа отдельных электронов" [65, с. 190]. При понижении сферической симметрии изолированного атома до аксиальной электроны, характеризующиеся одними и теми же квантовыми числами n и l, но различными |m|[24], уже не будут эквивалентными. Их энергия теперь зависит также от абсолютной величины квантового числа m. Таким образом, атомная оболочка ns не расщепляется, в то время как оболочки np,nd,... расщепляются на две, три,... оболочек. Одна из них (σ-типа) характеризуется нулевым значением проекции одноэлектронного момента импульса на ось квантования. Она может заполняться не более чем двумя электронами с противоположными спинами. Каждой из остальных оболочек (π-, σ-...типов) соответствуют два не нулевых, равных по абсолютной величине, но различающихся знаком, значения проекции момента импульса. Соответственно эти оболочки могут заполняться не более чем четырьмя электронами.