или с учётом 1/c 2=ε 0μ 0и известного выражения для поля тока B=μ 0 I/2π rнайдём
F эл=qVB/1,5.
Это с точностью до множителя 1,5 даёт силу Лоренца F л=qVB. То есть и сила Лоренца имеет чисто электрическую природу. Ту же силу легко получить из БТР и для заряда, летящего перпендикулярно проводнику. Раз сила Лоренца не зависит от направления движения заряда, то и по теории Ритца заряд должен описывать в магнитном поле Bокружности, как того требует опыт.
Итак, надобность в магнитном поле отпадает, ибо то, что принято считать магнитной силой, всего лишь не скомпенсированная добавка силы электрической, созданная движением зарядов. В свою очередь, эта добавка — естественное следствие баллистической модели взаимодействия зарядов и механического сложения скорости распространения света и электрического воздействия (по сути скорости реонов) со скоростью источника. Другими словами, как это утверждали ещё Ампер и Ритц, магнитных сил и полей, вообще говоря, не существует. За их проявления мы ошибочно принимаем результат вызванного движением зарядов изменения электрических сил. Именно поэтому не удалось и никогда не удастся найти магнитные «заряды», — предсказанные Дираком монополи, существование которых казалось естественным следствием равноправия, обратимости полей и симметрии уравнений Максвелла. Выходит, что, вопреки Максвеллу, свет вполне может распространяться и без помощи магнитного поля. Наоборот, именно конечная скорость света, реонов и порождает магнитные эффекты.
Таким образом, баллистическая модель и теория Ритца не только согласуются со всеми электрическими и магнитными эффектами, но и позволяют в рамках классической картины мира понять их природу. Сама идея влияния движения заряда на величину электрической силы и объяснение через это магнитных эффектов возникла уже очень давно. Задолго до Ритца (как он сам же замечает [8]) её высказал Гаусс и развил Вебер, ещё в середине XIX века построивший на её основе электродинамику, рассматривающую магнитные и индукционные силы как следствие изменения (при движении и ускорении зарядов) сил электрических [72, 106]. Причём электродинамика Ампера и Вебера долгое время принималась учёными и противопоставлялась теории Максвелла.
Но концепция Вебера была отвергнута, причём, по иронии судьбы, — тем самым фактом, из которого должна бы была проистекать. Дело в том, что Вебер был сторонником теории дальнодействия, то есть мгновенного распространения воздействий, без помощи какого-либо промежуточного агента. А формулы свои, описывающие влияние движения на величину электрической силы, он не вывел, а эмпирически подобрал, основываясь на опытах [72, 106]. А между тем, как было показано, и как утверждал Гаусс (учитель Вебера), их можно вывести строго, придерживаясь прямо противоположного принципа, — считая, что воздействие передаётся не мгновенно, а с задержкой, через некий промежуточный агент (реоны). Предположение же о мгновенной передаче воздействия с бесконечной скоростью реонов ( c =∞), как легко проверить, привело бы, напротив, к постоянной, не зависящей от движения зарядов величине силы. Так Ритц обосновал подход Вебера и Гаусса и тем самым завершил процесс сведения магнитных эффектов к электрическим, начатый ещё Ампером. Именно Ампер впервые понял, что магнетизм — это фикция, и магнит представляет собой лишь набор элементарных молекулярных круговых токов, то есть, в конечном счёте, — движение зарядов. Таким образом, правильнее говорить не о связи электрических и магнитных эффектов, а о том, что вторые — это лишь частное проявление первых. Интересно, что гипотезу Ампера об электрической природе магнитных сил, как следствия взаимодействия элементарных токов тел, выдвигали ещё Демокрит с Лукрецием, объяснявшие магнитное воздействие ударами микрочастиц (реонов § 4.19), источаемых магнитами и электроном (янтарём).
В том, что магнитное поле — это фикция, легко убедиться, рассмотрев два пучка электронов, летящих параллельно с одинаковой скоростью. По Максвеллу это движение зарядов создаст магнитное поле, отчего между пучками, кроме кулоновской силы отталкивания, возникнет ещё сила магнитного притяжения, как между двумя токами. Но если перейти в подвижную систему отсчёта, связанную с летящими электронами, магнитная сила исчезнет, хотя сила взаимодействия пучков по классическому принципу относительности должна остаться прежней. Свести концы с концами в теории Максвелла удаётся лишь посредством теории относительности, по которой исчезновение магнитного притяжения в точности компенсируется релятивистским снижением кулоновского отталкивания пучков [96]. Совсем как в опыте Майкельсона, где пытались объяснить отсутствие перемен при изменении скорости тем, что оно в точности компенсируется сокращением плеч интерферометра, пока не поняли, что справедлив принцип относительности (§ 1.9). Но, раз справедлив этот открытый Галилеем принцип, не проще ли считать, что и электрическая сила взаимодействия пучков не зависит от того, в какой системе она измерена, тогда как магнитная сила вообще не возникает? И действительно, электрическая сила по Ритцу, как видели, зависит не от абсолютной скорости зарядов в некой системе отсчёта, а лишь от их взаимной скорости по отношению друг к другу. Именно эта зависимость, доказывающая, что заряд сообщает свою скорость воздействиям, и воспринимается нами в форме магнитных эффектов.
Идея чисто электрической природы магнитных сил всегда лежала на поверхности, отчего многократно переоткрывалась и в наше время. Ведь любой знает, что магнитные силы порождаются движением зарядов, откуда один шаг до мысли, что изменение кулоновского взаимодействия зарядов от их движения и создаёт магнитные эффекты за счёт конечной световой скорости электрических воздействий и запаздывающих потенциалов. Не случайно, с этой идеей, высказанной ещё Гауссом, Вебером и развитой Ритцем, независимо выступали многие учёные, в том числе Н.К. Носков, В.М. Петров [96]. Кстати, В. Петров, рассматривая взаимодействие проводников, ещё в 2004 г. выдвинул ряд интересных идей, в том числе о неравномерном распределении движущихся электронов по металлу, что позволяет решить ряд затруднений теории Ритца, скажем при объяснении явлений индукции, самовоздействия тока электронов, а также формы закона Ампера и значения коэффициента в нём.
Следует заметить, что теории Вебера и Ритца приводят к закону взаимодействия токов, отличному от общепринятого. Так, считается, что магнитные силы всегда перпендикулярны элементам тока (Рис. 17). Но это нарушает принцип действия и противодействия, особенно если один ток идёт вдоль, а другой поперёк соединяющей их линии MN; здесь одна из сил — вообще нулевая. В теории же Вебера силы магнитного взаимодействия всегда равны и противоположно направлены. Да и сам Ампер, открывший взаимодействие токов, утверждал, что магнитные силы действуют вдоль линии, соединяющей элементы. Конечно, и в теории Ритца сила действия порой не равна силе противодействия и они направлены не строго вдоль линии, соединяющей элементы или заряды (§ 1.17, § 3.17). Но это вызвано конечной скоростью воздействий и, в отличие от закона Био-Савара, не противоречит закону сохранения импульса, если учесть импульс, несомый реонами, летящими в пространстве меж элементами тока. Поэтому экспериментально найденный Ампером и подтверждённый Вебером закон взаимодействия токов [106], равно как закон, вытекающий из теории Ритца, не совпадает с общепринятым закона Био-Савара-Лапласа, следующим из теории Максвелла.
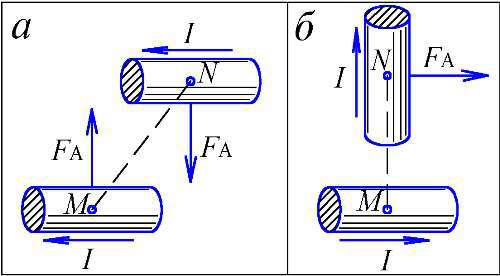
Рис. 17. Нарушение 3-го закона Ньютона общепринятым законом взаимодействия параллельных (а) и перпендикулярных (б) токов: силы направлены под углом к линии связи MN, а в случае б в точке M сила вообще отсутствует.