Отметим, что ключ к пониманию селективного и простого фотоэффекта, на основе волновой теории, был предложен ещё П. Друде, который развил классическую теорию проводимости металла, на основе модели электронного газа (§ 4.17). Именно Друде открыл, что свет, отражённый металлом, поляризуется, словно при отражении диэлектриком, что доказывает преимущественное пропускание и поглощение металлом света одной поляризации [136]. Однако, Друде вскоре после разработки этих теорий трагически умер в 1906 г. в возрасте 42-х лет, как считают, — в результате самоубийства [161]. Это не только позволило спокойно расправиться с его классическими теориями металлооптики и проводимости, но и открыло дорогу теории относительности и квантовой теории на страницы редактируемого им журнала "Анналы физики", — одного из ведущих в то время.
§ 4.5 Нелинейный фотоэффект
Вот уже более пятнадцати лет развивается новое научно-техническое направление, связанное с умножением оптических частот (применяется также термин "генерация оптических гармоник": второй гармоники, третьей, четвёртой и т. д. — в зависимости от того, во сколько раз умножается частота исходного лазерного излучения).
Л.В. Тарасов, "Что такое нелинейная оптика" [143]
Другая важная разновидность фотоэффекта — нелинейный фотоэффект, чаще называемый ошибочно — "многофотонным". Суть его в том, что мощное лазерное излучение частоты fвыбивает электроны с энергией уже не hf, а — удвоенной и кратной энергии E= nhf, где n— целое число [74]. Это принято объяснять тем, что в лазерном излучении плотность потока света столь высока, что электрон, порой, поглощает не один, а сразу nфотонов, у каждого забирая энергию E= hf, потому эффект и называют ещё "многофотонным". И, всё же, этот эффект легко объясним в рамках волновой оптики. Металл под действием лазерного излучения генерирует, за счёт нелинейных эффектов, излучение удвоенной и других кратных частот. Вторичное излучение и выбивает электроны из металла. В отличие от принятого многофотонного объяснения, это позволяет понять, почему нелинейный фотоэффект вызывает, опять же, лишь нормальная к металлу компонента поля волны. То есть, нелинейный фотоэффект, подобно селективному, чувствителен к поляризации света (§ 4.4). Это означает, что и здесь свет вырывает электроны не с поверхности, а из толщи металла, проникая вглубь.
Как раз тот факт, что какую-то роль играет поляризация излучения, направление колебаний поля, — доказывает, что нелинейный, а, значит, и простой (линейный) фотоэффект связан с волновыми свойствами света [74]. Об этом говорит и тот факт, что эффект проявляется только под воздействием мощного лазерного излучения, когда в среде возникают нелинейные эффекты и колебания. А, раз дело в волнах, колебаниях, то фотоны уже не к месту.
В самом деле, давно известны среды, генерирующие в свете лазерного луча излучение с удвоенной, утроенной и, вообще, — кратной частотой. Этот нелинейный эффект, чисто классически следующий из нелинейной теории колебаний [103], называют умножением оптических частот или генерацией оптических гармоник [143, с. 110]. Так, инфракрасный луч, упав на кристалл ниобата лития, выходит из него уже зелёным. Видимо, то же происходит и в нелинейном фотоэффекте: луч, упав на границу полупроводника или металла, рождает излучение удвоенной и кратной частоты nf. Это вторичное излучение и выбивает электроны кратных энергий hnf(Рис. 155). Нелинейный и селективный фотоэффекты потому и зависят от направления световых колебаний относительно среды, что электроны выбивает вторичное, преобразованное средой излучение. Так, в селективном фотоэффекте резонанс излучения в веществе избирательно усиливает пропускание света в определённом диапазоне, наращивая фототок на данной частоте (§ 4.4). А в нелинейном фотоэффекте среда генерирует излучение кратных частот. Итак, фотоэффект легко объясним в рамках волновой теории света, и фотоны с квантами здесь излишни.
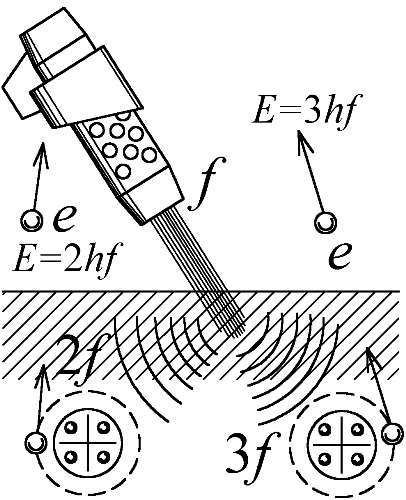
Рис. 155. Нелинейный фотоэффект.
Вообще, нелинейные эффекты в оптике сейчас любят сводить к квантовым. Так, генерацию второй гармоники в нелинейной среде (чисто волновое явление) теперь зачем-то объясняют сложением двух фотонов в один, но с удвоенной энергией, вдобавок с переходом через несуществующий виртуальный уровень. Никто не наблюдал такого сложения фотонов в свободном пространстве: для него всегда требуется вещество, среда, а, значит, не в фотонах дело, а как раз в среде. Об этом говорит ещё и тот факт, что интенсивность второй гармоники существенно зависит от нелинейных характеристик среды. Так, есть среды с кубичной нелинейностью, которые легко генерируют третью гармонику и намного хуже — вторую, хотя, по квантовой теории, всё было бы наоборот, поскольку двум фотонам сложиться проще, чем сразу трём. То же касается двух- и многофотонного поглощения, нелинейного фотоэффекта, где реально происходит не захват многих фотонов, а поглощение излучения кратной частоты, сгенерированного средой, под напором лазерного света. Таким образом, следуя принципу Оккама, не стоит умножать сущностей сверх необходимого. Раз для объяснения фотоэффекта, включая селективный и нелинейный, вполне достаточно классической волновой теории, то ни к чему придумывать кванты света и фотоны, противоречащие ряду особенностей фотоэффекта. Зачем огород городить и квантовать, раз и без этого всё вполне понятно? Если бы причина была в поглощении электроном нескольких фотонов, то нелинейный фотоэффект интенсивней всего шёл бы на поверхности металла, где интенсивность света и пропорциональная ей вероятность многофотонных процессов — выше. А, на деле, как показывает чувствительность фотоэффекта к поляризации излучения, свет вырывает электроны из толщи металла, подтверждая волновую природу фотоэффекта.
Интересно, что нелинейный эффект генерации разностных или суммарных (в том числе кратных) частот от сложения двух колебаний, гораздо раньше, чем в оптике, был открыт и исследован в акустике (тоны Гельмгольца [72]). Никому и в голову не придёт объяснять этот эффект сложением квантов звука (гипотетических фононов), поскольку эффект легко объясним классической нелинейной теорией колебаний. Однако, когда и в оптике, наконец, выявили генерацию разностных и суммарных частот света (скажем, в рамановском комбинационном рассеянии), то учёные почему-то прибегли к квантовой трактовке эффекта, по принципу сложения и деления квантов света, хотя существовала готовая теория взаимодействия световых колебаний в нелинейных средах и соотношения Мэнли-Роу. Таким образом, квантовая теория эффекта Рамана и умножения оптических частот не только не нужна, но даже вредна, поскольку вводит избыточные и ошибочные утверждения, мешающие правильному пониманию процессов и их точному описанию.
Так, только волновая, колебательная трактовка объясняет тот факт, что для нелинейного фотоэффекта существует зависимость величины фототока от направления поляризации падающего света, совсем как в селективном фотоэффекте (§ 4.4). Раз преобразование излучения во вторую гармонику — это обычный нелинейный волновой эффект, протекающий в веществе (любое вещество в сильных лазерных полях становится нелинейной средой), то излучение должно прежде проникнуть в среду. А это, как видели, возможно лишь для света с продольной поляризацией, проникающего в толщу металла и выбивающего электроны уже не только с поверхности. Действительно, свет высокой интенсивности, даже при сильном затухании, способен сравнительно глубоко проникать в металл. Интенсивный свет, прошедший в глубь металла, и создаёт нелинейные эффекты. Удвоение частоты может происходить как в объёме металла, так и в отдельных его кристаллах, ориентированных случайным образом, в том числе, — таким, который обеспечивает выполнение условия синхронизма и эффективное преобразование первой гармоники во вторую. Итак, прозрачность металла — вещь относительная. Вдобавок в сильных лазерных полях, за счёт эффекта просветления среды, даже непрозрачная среда может стать отчасти прозрачной. Именно это позволило, в своё время, создать полупроводниковые лазеры, хотя полупроводники непрозрачны для света и во многом сходны по свойствам с металлами, что, как полагали кванторелятивисты, делает полупроводник непригодным в качестве активной среды лазера (§ 4.9). Таким образом, фотоэффект, часто называемый "многофотонным", гораздо правильней называть "нелинейным", как у Ландсберга [74]. Нелинейный фотоэффект — это чисто волновое, колебательное, классическое явление, относящееся к нелинейной оптике.