В целом видим, что какими бы великими ни казались поначалу сложности механической модели взаимодействия зарядов, отмеченные ещё Ритцем, их можно решить. Во времена Ритца эти трудности казались неустранимыми, поскольку не было ещё известно о распадах элементарных частиц, об античастицах и антиматерии, имевшей по исходной гипотезе Дирака минусовую массу. И, всё же, Ритц осмелился выступить со своей революционной моделью обменного взаимодействия зарядов, посредством испускаемых ими частиц.
§ 1.7 Природа магнетизма
Пуанкаре показал, что, придав лучистой энергии импульс, всё можно поставить на свои места. Очевидно, что такое предположение вполне естественно, если эта энергия испускается [в виде частиц], а не распространяется [в среде]… Исходя из этих принципов, получится вывести электродинамические силы, зависящие от скорости и ускорения, руководствуясь лишь кинематическими соображениями. Именно эту проблему, не решённую теорией Максвелла, Гаусс поставил в своём известном послании к В. Веберу.
Вальтер Ритц, "Критический анализ общей электродинамики" [8]
Что собой представляют электрические и магнитные воздействия? Современная физика, к несчастью, не может ответить на этот вопрос, оправдывая свою беспомощность ньютоновской отговоркой: «Довольно и того, что эти силы существуют и действуют согласно изложенным законам» (в электродинамике этими законами служат уравнения Максвелла). И только баллистическая теория Ритца, как было показано выше, впервые в истории науки наглядно объяснила, как же взаимодействуют заряды. Ритц не просто описал электрическое взаимодействие, а нашёл его глубинные причины, начала: вскрыл механизм взаимодействия. Но как же он объяснил взаимодействие магнитное? Чтобы понять это, снова рассмотрим взаимодействие двух элементарных зарядов.
Напомним, как по Ритцу протекает взаимодействие двух электронов. Первый электрон излучает, выстреливает по всем направлениям со скоростью света cособые микрочастицы — реоны. Спустя время часть их долетает до второго электрона и поглощается им, причём каждый реон передаёт электрону элементарную порцию (квант) воздействия — стандартный импульс p. Полная сила отталкивания электронов
F = np,
где n— частота попаданий реонов в электрон, а p— импульс, передаваемый каждым реоном. Если скорость реонов — V, а их масса — m, то
p = mV.
Частота попаданий в площадку S, перпендикулярную потоку частиц, находится как
n = kVS,
где k— концентрация частиц в потоке, а V— скорость их потока. Отсюда
F = np = kV 2Sm.
Для электрона в потоке реонов (от неподвижного электрона) скорость частиц V= c, а S— площадь поперечного сечения электрона, откуда
F = np = kcSp = kc 2Sm.
С удалением от электрона концентрация kвыстреленных им реонов убывает пропорционально квадрату расстояния (Рис. 11). Отсюда, как выяснили выше, и следует закон Кулона: сила Fотталкивания электронов спадает, пропорциональна квадрату расстояния между ними (§ 1.4).
Рис. 11. Один электрон действует на другой через посредство выстреливаемых им реонов R, воздействие которых спадает вместе с их концентрацией k пропорционально квадрату расстояния.
Так теория Ритца объясняет силу электростатического взаимодействия зарядов. Ну а магнитные силы возникают, как известно, от движения электрических зарядов. Физики говорят, что в зависимости от движения зарядов их электрическое поле преобразуется в магнитное и наоборот (поэтому говорят об электромагнитном поле, считая электричество и магнетизм лишь различными его проявлениями). Но как происходит этот переход, почему его вызывает движение зарядов, и что вообще такое магнетизм, современная физика объяснить не может. Теория же Ритца даёт на это простой и ясный ответ.
Выше было показано, что два неподвижных заряда взаимодействуют с силой F= kc 2Sm. Теория Ритца предсказывает изменение этой силы при сближении зарядов. Если один заряд движется, закон Кулона оказывается не вполне точен, что связано с конечной скоростью света, реонов, переносящих электрическое воздействие. В самом деле, пусть электрон, испускающий реоны, покоится, а другой движется ему навстречу со скоростью v. В таком случае скорость потока V, с которой реоны ударяются об электрон, согласно классической механике, будет равна уже не c, но V=c΄=c+v. Соответственно вырастет и импульс, передаваемый реонами электрону и частота их ударов, а, в конечном счёте, и сила отталкивания одного электрона другим. Из-за увеличения скорости Vвстречного потока реонов от cдо c΄=c+vполучим F= k(c+v) 2Sm. Сила вырастет по сравнению с той, что испытывали бы покоящиеся заряды на том же удалении. Напротив, расхождение зарядов уменьшит эту силу. Именно это небольшое изменение силы электростатического взаимодействия и воспринимается нами как магнитное воздействие. Причину этих изменений поясняет баллистическая модель: броневик, расстреливающий неподвижную мишень, увеличивает свою огневую мощь, когда быстро едет навстречу цели (Рис. 12). Ведь при движении к мишени растёт частота ударов и скорость пуль, а значит и сила ударов по мишени: пули барабанят по мишени чаще и сильнее. Ещё заметней будет эффект для пулемёта, установленного на самолёте, скорость которого уже сравнима со скоростью пуль.
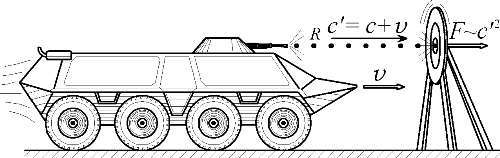
Рис. 12. Подобно огневой силе движущегося броневика, повышена сила F взаимодействия сближающихся со скоростью v зарядов за счёт выросшей скорости c'=c+v и частоты ударов реонов R.
Далее рассмотрим заряженную нить и возле неё в т. Oзаряд q. Сила отталкивания заряда от нити
F= qτ/2πε 0r,
где τ— линейная плотность заряда нити, r— расстояние от заряда до нити, а ε 0— электрическая постоянная. Сила же взаимодействия заряда с малым участком нити Mдлиной dl, имеющим заряд τ dl, даётся законом Кулона
F= qτ dl/4πε 0 OM 2.
Перпендикулярная нити составляющая этой силы выразится через углы φи dφкак
F у= qτcos(φ)dφ/4πε 0r(Рис. 13).
Найдём, как изменится сила при движении заряда параллельно нити со скоростью v. По отношению к движущемуся заряду встречные реоны будут иметь скорость c΄отличную от cза счёт векторного вычитания из c скорости v заряда. И направлена скорость c΄ реонов будет уже не вдоль MO, а вдоль M΄O(ту же природу имеет звёздная аберрация — отклонение световых лучей, вызванное движением Земли, § 1.9). Из треугольника скоростей OMM΄:
c΄= [c 2+v 2–2cvsin(φ)] 1/2
или, разлагая в ряд и считая v/cмалым, получим
c΄≈ с[1–sin(φ)v/c+(v/c) 2cos 2(φ)/2].
Соответственно меняется и сила:
F΄=F(c΄/c) 2.
Но, поскольку сила меняет и направление ( F΄ действует вдоль c΄ ), то интересующая нас составляющая F уизменится в несколько меньшей степени:
F у΄= F у(c΄/c) = [1–sin(φ)v/c+ (v/c) 2cos 2(φ)/2]cos(φ)dφqτ/4πε 0r.
Остаётся найти суммарную силу воздействия на заряд со стороны всех элементов нити, проинтегрировав F у΄в пределах φ от — π/2до +π/2. В итоге, полная сила