Чаще всего к М. ф. прибегают при исследовании различных механических (включая гидроаэромеханику и механику деформируемого твёрдого тела), тепловых и электродинамических явлений. При этом число и вид критериев подобия для каждого моделируемого явления зависит от его природы и особенностей. Так, например, для задач динамики точки (или системы материальных точек), где все уравнения вытекают из второго закона Ньютона, критерием подобия является число Ньютона Ne = Ft²/ml и условие М. состоит в том, что

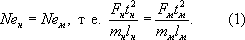
  Для колебаний груза под действием силы упругости F = cl равенство (1) приводит к условию t²_нс_н/m_н = t²_мс_м/m_м , что, например, позволяет по периоду колебаний модели определить период колебаний натуры; при этом явление не зависит от линейного масштаба (от амплитуды колебаний). Для движения в поле тяготения, где F = km/l² , условием подобия является k_нt²_н/l³_н = k_мt²_м/l³_м (явление не зависит от масс). При движении в одном и том же поле тяготения, например Солнца, k_м = k_н , и полученное соотношение даёт третий закон Кеплера для периода обращения. Отсюда, считая одну из планет «моделью», можно, например, найти период обращения, любой другой планеты, зная её расстояние от Солнца.

  Для непрерывной среды при изучении её движения число критериев подобия возрастает, что часто значительно усложняет проблему М. ф. В гидроаэромеханике основными критериями подобия являются Рейнольдса число Re , Маха число М , Фруда число Fr , Эйлера число Еu , а для нестационарных (зависящих от времени) течений ещё и Струхаля число St . При М. ф. явлений, связанных с переносом тепла в движущихся жидкостях и газах или с физико-химическими превращениями компонентов газовых потоков и др., необходимо учитывать ещё ряд дополнительных критериев подобия.

  Создаваемые для гидроаэродинамического моделирования экспериментальные установки и сами модели должны обеспечивать равенство соответствующих критериев подобия у модели и натуры. Обычно это удаётся сделать в случаях, когда для течения в силу его особенностей сохраняется лишь один критерий подобия. Так, при М. ф. стационарного течения несжимаемой вязкой жидкости (газа) определяющим будет параметр Re и необходимо выполнить одно условие

где r — плотность, m — динамический коэффициент вязкости среды. При уменьшенной модели (l_м < l_н ) это можно сделать, или увеличивая скорость (v_м > v_н ), или используя для моделирования другую жидкость, у которой, например, r_м > r_н , а m_м £ m_н . При аэродинамических исследованиях увеличивать v_м в этом случае нельзя (нарушится условие несжимаемости), но можно увеличить r_м , используя аэродинамические трубы закрытого типа, в которых циркулирует сжатый воздух.

  Когда при М. ф. необходимо обеспечить равенство нескольких критериев, возникают значительные трудности, часто непреодолимые, если только не делать модель тождественной натуре, что фактически означает переход от М. ф. к натурным испытаниям. Поэтому на практике нередко прибегают к приближённому моделированию, при котором часть процессов, играющих второстепенную роль, или совсем не моделируется, или моделируется приближённо. Такое М. ф. не позволяет найти прямым пересчётом значения тех характеристик, которые не отвечают условиям подобия, и их определение требует соответствующих дополнительных исследований. Например, при М. ф. установившихся течений вязких сжимаемых газов необходимо обеспечить равенство критериев Re и М и безразмерного числа c = c_p /c_v (c_p и c_v — удельные теплоёмкости газа при постоянном давлении и постоянном объёме соответственно), что в общем случае сделать невозможно. Поэтому, как правило, обеспечивают для модели и натуры лишь равенство числа М , а влияние на определяемые параметры различий в числах Re и c исследуют отдельно или теоретически, или с помощью других экспериментов, меняя в них в достаточно широких пределах значения Re и c.

  Для твёрдых деформируемых тел особенности М. ф. тоже зависят от свойств этих тел и характера рассматриваемых задач. Так, при моделировании равновесия однородных упругих систем (конструкций), механические свойства которых определяются модулем упругости (модулем Юнга) Е и безразмерным Пуассона коэффициентом n, должны выполняться 3 условия подобия:

где g — ускорение силы тяжести (g = rg — удельный вес материала). В естественных условиях g_м = g_н = g , и получить полное подобие при l_м ¹ l_н можно, лишь подобрав для модели специальный материал, у которого r_м , Е_м и n_м будут удовлетворять первым двум из условий (3), что практически обычно неосуществимо.

  В большинстве случаев модель изготовляется из того же материала, что и натура. Тогда r_м = r_н , Е_м = Е_н и второе условие даёт g_мl_м = g_нl_н . Когда весовые нагрузки существенны, для выполнения этого условия прибегают к т. н. центробежному моделированию, т. е. помещают модель в центробежную машину, где искусственно создаётся приближённо однородное силовое поле, позволяющее получить g_м > g_н и сделать l_м < l_н . Если же основными являются другие нагрузки, а весом конструкции и, следовательно, учётом её удельного веса g = rg можно пренебречь, то приближённое М. ф. осуществляют при g_м = g_н = g , удовлетворяя лишь последнему из соотношений (3), которое даёт F_м/l²_м = F_н/l²_н , следовательно, нагрузки на модель должны быть пропорциональны квадрату её линейных размеров. Тогда модель будет подобна натуре и если, например, модель разрушается при нагрузке F_кр , то натура разрушается при нагрузке F_крl_н/l_м . Неучёт в этом случае весовых нагрузок даёт следующее. Поскольку эти нагрузки имеют значения gl³ , а последнее из условий (3) требует пропорциональности нагрузок Р , то при l_м < l_н весовая нагрузка на модель будет меньше требуемой этим условием, т. е. М. ф. не будет полным и модель, как недогруженная, будет прочнее натуры. Это обстоятельство тоже можно учесть или теоретическим расчётом или дополнительными экспериментами.

  Одним из видов М. ф., применяемым к твёрдым деформируемым телам, является поляризационно-оптический метод исследования напряжений, основанный на свойстве ряда изотропных прозрачных материалов становиться под действием нагрузок (т. е. при деформации) анизотропными, что позволяет исследовать распределение напряжений в различных деталях с помощью их моделей из прозрачных материалов.

  При М. ф. явлений в других непрерывных средах соответственно изменяются вид и число критериев подобия. Так, для пластичных и вязкопластичных сред в число этих критериев наряду с параметрами Фруда, Струхаля и модифицированным параметром Рейнольдса входят параметры Лагранжа, Стокса, Сен-Венана и т. д.