Ну, действительно: как измеряют количество теплоты? Его измеряют калориметрическим методом – через приращение температуры балластного вещества, когда считаются известными его масса и теплоёмкость. А как измеряют теплоёмкости? Их измеряют тоже калориметрическим методом – через приращение температуры балластного вещества, когда считаются известными его масса и сообщённое ему количество теплоты. Выходит, что тепловые эффекты и теплоёмкости, связанные законом Кирхгофа (5.11.1), образуют, с эмпирической точки зрения, тривиальный замкнутый круг. Хуже того: соответствия между справочными температурными зависимостями теплоёмкостей и тепловых эффектов зачастую обеспечивались прямыми пересчётами, при множественных согласованиях экспериментальных результатов для одних и тех же веществ, участвующих в различных реакциях. По результатам этой титанической работы, в которой задействованы целые институты, закон Кирхгофа подтверждается, в основном, благодаря калькуляциям – выполненным именно так, как требует этот самый закон!
Такое положение дел неудивительно. Выше мы уже приводили свидетельства о том, что энергии химических связей являются иллюзиями (5.7,5.8). Теперь мы изложим наши представления о источниках тепла химических реакций. Мы говорим «о источниках», а не «о источнике» - вот почему. Известно, во-первых, множество реакций со слабыми тепловыми эффектами. Такие реакции, как правило, термодинамически обратимы – в условиях химического равновесия, количества элементарных актов прямой и обратной реакций, экзотермической и эндотермической, в среднем, одинаковы, и температура среды остаётся постоянной. Но известно, во-вторых, множество реакций с большим тепловым выходом – в частности, реакций горения. Они термодинамически необратимы: здесь, насколько нам известно, не бывает равновесий между прямой и обратной реакциями, причём, в обратной реакции не происходит эквивалентного «поглощения тепла». С позиций термодинамики, совершенно необъяснимо, почему при слабых тепловых эффектах названная обратимость имеет место, а при сильных – нет. Между тем, этот парадокс легко разрешается: ниже мы постараемся показать, что главный источник тепла при реакциях горения – совсем не тот, что при обратимых реакциях со слабым тепловым выходом.
Заметим, что известно множество экзотермических реакций пересоединения, при которых образованию связей у продуктов предшествует разрыв связей у реагентов. Тепловой выход здесь объясняют более сильными связями у продуктов по сравнению с реагентами. На первый взгляд, всё логично: реакция идёт в таком направлении, чтобы результирующая конфигурация оказывалась в сильнее связанном состоянии, чем исходная. Но эта исходная конфигурация не может самопроизвольно «скатиться» в более глубокую потенциальную яму. Молекулы реагентов имеют собственный запас устойчивости – скажем, в несколько эВ – и этот запас устойчивости определяет высоту энергетического барьера, который необходимо преодолеть этим молекулам, чтобы могло произойти химическое превращение. Полагают, что молекулы реагентов попадают на вершину этого энергетического барьера, приобретая т.н. энергию активации [Ф3,Б1]. Так, для реакций в газовой фазе, энергия активации приобретается, например, в результате столкновений молекул, скорости которых соответствуют высоко-скоростному «хвосту» максвелловского распределения. При таком столкновении, якобы, временно формируется т.н. активированный комплекс [П2] – из вмазанных друг в друга молекул реагентов – и этот комплекс скатывается в более связанное состояние, т.е. химические связи переформировываются, после чего продукты реакции разлетаются. Но эта механистическая модель, на наш взгляд, несостоятельна [Г3].
Тепловые эффекты у обратимых реакций с малым тепловым выходом.
Наблюдая метаморфозы неодушевлённого вещества, мы видим, что в результате реакций синтеза, типа А+В->АВ, происходит, как правило, повышение температуры в зоне реакции, а в результате реакций распада, типа АВ->А+В, происходит, как правило, понижение температуры в зоне реакции. Главная причина этих повышений-понижений температуры, на наш взгляд – отнюдь не «выделение тепла» при образовании химических связей и не «поглощение тепла» при их разрыве. Мы полагаем, что в данных случаях происходят процессы, которые являются проявлениями принципа Ле Шателье: «если первоначальные условия, при которых система находится в состоянии равновесия, изменяются, то равновесие смещается в направлении, способствующем восстановлению первоначальных условий» [П2]. Только мы трактуем этот принцип несколько шире, чем это обычно делается.
Действительно, рассмотрим такую равновесную систему, как смесь двух газов, в которой пока ещё не идёт реакция синтеза. Пусть эта смесь находится в закрытом сосуде. При термодинамическом равновесии, энергообмен между содержимым сосуда и его стенками происходит так, что поток энергии от газов к стенкам в точности скомпенсирован потоком энергии от стенок к газам. Теперь, пусть в смеси газов начинается реакция синтеза – в ходе которой, концентрация молекул в сосуде, очевидно, уменьшается. Если при этом средняя кинетическая энергия молекул оставалась бы прежней, то поток энергии, передаваемый ими стенкам сосуда, уменьшался бы. Результирующее нарушение равновесия восстанавливается, согласно принципу Ле Шателье, через такое перераспределение между различными составляющими внутренней энергии смеси, при котором средняя кинетическая энергия молекул увеличивается – что и означает повышение температуры смеси.
Оценим максимальную величину этого эффекта при допущении, что энергообмен между содержимым сосуда и его стенками обусловлен лишь ударами молекул газов о стенки. В качестве мощности W* энергообмена примем произведение средней кинетической энергии молекул газов на эффективное число их ударов, приходящихся на участок площади стенки за единицу времени. Будем считать, что эффективное число ударов определяется числом движущихся к стенке молекул, содержащихся в пристеночном слое с толщиной, равной длине свободного пробега молекул – причём это число ударов происходит за промежуток времени, равный частному от деления толщины пристеночного слоя на среднюю скорость молекул. Тогда для случая, когда в сосуде содержатся однотипные молекулы, величина W* пропорциональна произведению nSmV3, где n – концентрация молекул, S – площадь участка стенки, m и V – масса и средняя скорость молекулы. Используя известное соотношение молекулярно-кинетической теории mV2=3kT, получаем, что W*~nS(3kT)3/2m-1/2. Для предельного случая, т.е. полного превращения одноатомного газа в двухатомный – например, при реакции Н+Н->Н2 – условие сохранения мощности энергообмена даёт нам равенство
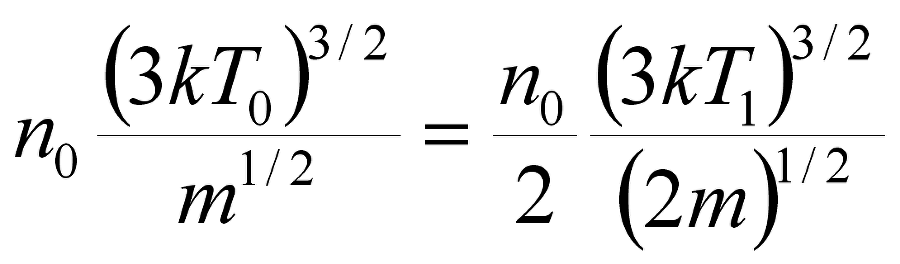
, (5.11.2)
где нулевые индексы означают исходные значения, T1 – конечная температура. Из (5.11.2) следует, что T1=81/3·T0=2T0, т.е. полному превращению газа из одноатомного в двухатомный соответствует увеличение его температуры вдвое – причём, к этому результату не имеют никакого отношения ни теплоёмкости исходного и конечного газов, ни «энергия химической связи» у молекул второго из них. Конечно, двукратное локальное повышение температуры в результате реакции синтеза – и, аналогично, двукратное локальное понижение температуры в результате реакции распада – это теоретические идеализации. Практические изменения температуры ΔT, как результаты реакций синтеза-распада, должны быть гораздо меньшими. Принцип Ле Шателье задаёт лишь направление процессов, компенсирующих уход от равновесия – отнюдь не утверждая, что компенсация будет стопроцентной. И, обратим внимание: если результирующее изменение температуры прямо пропорционально исходной температуре, т.е. ΔT=ξT0, где ξ<<1, то не здесь ли скрывается источник главных частей температурных зависимостей у «тепловых эффектов»? Ведь величины «тепловых эффектов», как правило, увеличиваются по мере повышения температуры – как у экзотермических реакций, так и у эндотермических!