Рис.5.1.1

Как можно видеть, атом, имеющий в своём составе равные количества носителей элементарных зарядов обоих знаков, при статическом зарядовом разбалансе даже в одной своей связке «протон-электрон», способен вести себя как обладатель ненулевого эффективного заряда – на интервалах времени, больших по сравнению с периодом прерываний, который для внешних атомарных электронов составляет ~10^-15 с.

Первое, что модель зарядовых разбалансов помогает нам прояснить – это природа тех энергий возбуждения в атоме, которые попадают в континуум между квантовыми уровнями. Квантовая теория отказывает в существовании этому континууму – полагая, что энергия возбуждения может соответствовать только дискретным стационарным уровням. Но, как мы уже излагали выше (3.1), этот подход квантовой теории, с точки зрения практики, избыточно категоричен. Атомные спектральные линии соответствуют резонансным переходам, с одного квантового уровня на другой – происходящим с наибольшими вероятностями – но квантовые переходы с участием промежуточного континуума, несомненно, тоже происходят (3.1). Поэтому адекватные представления об атомных структурах должны пояснять расклад энергий для ситуаций, при которых энергия связи атомарного электрона соответствует некоторому значению из континуума между квантовыми уровнями.

Как мы излагали выше (4.9), размер атомарной связки «протон-электрон», которая имеет энергию связи, соответствующую тому или иному возбуждённому стационарному состоянию, равен её размеру в основном состоянии. Иными словами, радиус атома, при нахождении электрона на любом квантовом уровне энергии, один и тот же – и равен радиусу в основном состоянии. Логично допустить, что и при наличии у электрона энергии, попадающей в континуум между квантовыми уровнями, радиус атома остаётся прежним. Тогда, рассмотрим случай наличия у связки «протон-электрон» энергии возбуждения, попадающей в континуум между основным и первым стационарным уровнями. Если размер связки «протон-электрон» при этом равен размеру в основном состоянии, то, согласно (4.9.1), и частота атомных прерываний такова же, как в основном состоянии, и, соответственно, собственные энергии протона и электрона в этой связке таковы же, как в основном состоянии. Но поскольку энергия их связи при этом уменьшена на величину энергии возбуждения, то нам придётся допустить, что энергия возбуждения – это какая-то особая форма энергии, о которой мы не говорили прежде. Мы полагаем, что это – энергия колебаний зарядового разбаланса, причём эти колебания обусловлены колебаниями скважности у прерываний, связующих протон и электрон. Сразу заметим, что у этих колебаний скважности могут варьироваться два параметра: размах и частота. Соответственно, и энергия этих колебаний скважности должна зависеть, вообще говоря, от тех же двух параметров – как и энергия классических осцилляций. Однако, при поглощении атомом нерезонансного кванта света и соответствующем попадании энергии возбуждения атома в междууровневый континуум, энергия этого кванта должна быть беспроблемно превращаема в энергию колебаний зарядового разбаланса, и обратно. Поскольку энергия кванта света зависит только от частоты, логично допустить, что беспроблемная превращаемость имеет место, если энергия колебаний зарядового разбаланса точно так же зависит только от частоты. Такое возможно, если, какова бы ни была энергия поглощённого нерезонансного кванта, размах результирующих колебаний зарядового разбаланса является одним и тем же – и мы полагаем, что он при этом максимален. Т.е., мы полагаем, что энергия hf нерезонансного кванта света равна энергии колебаний зарядового разбаланса, происходящих с частотой f и с полным размахом изменения скважности попеременных прерываний: от 0% до 100%. При таком раскладе вырисовывается, на наш взгляд, простейшая «сшивка» логики «цифрового» микромира и «аналогового» макромира. Действительно, энергии квантовых пульсаций, т.е. неопределённо долгой цепочки мгновенных смен двух состояний, ставится в соответствие энергия неопределённо долгих гармонических колебаний – причём, одинаковые приращения этих двух энергий вызываются одинаковыми приращениями их частот!

Такой подход позволяет прояснить вопрос, который может показаться риторическим – зачем в атоме требуются возбуждённые стационарные уровни энергии. Но неспроста же они организованы! Пусть связка «протон-электрон», находившаяся в основном состоянии (ground state), испытывает нерезонансное возбуждение, энергия которого попадает в континуум над основным уровнем. При этом расклад энергий таков: собственные энергии протона и электрона те же, что и в основном состоянии, а энергия их связи уменьшена на величину энергии возбуждения, т.е. на величину энергии колебаний зарядового разбаланса – с полным размахом. Тогда, как можно видеть, частота этих колебаний зарядового разбаланса имеет ограничение сверху. Действительно, на один период T₀ связующих прерываний всегда приходится лишь одно значение скважности, и минимальное число этих периодов, на протяжении которых скважность может измениться с полным размахом, равно двум: на одном периоде скважность равна 0%, а на другом – 100%. Таким образом, частота колебаний зарядового разбаланса, равная половине частоты связующих прерываний, является максимально возможной – при этом энергия возбуждения равна половине энергии связи в основном состоянии. Картина электронных пульсаций в связке «протон-электрон» для этого случая приведена на левой части Рис.5.1.2.

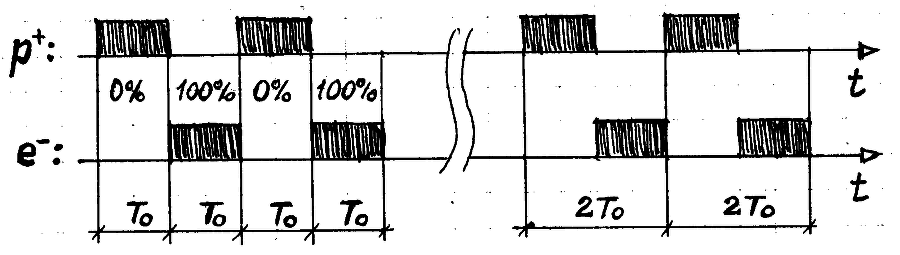
Рис.5.1.2 Высокочастотное заполнение – электронные пульсации.

Поразительным образом, эта картина идентична картине, имеющей место при половинной частоте связующих прерываний и отсутствии колебаний зарядового разбаланса – т.е. при чистом случае вдвое меньшей энергии связи (правая часть Рис.5.1.2). Такое совпадение мы расцениваем как свидетельство о самосогласованности и правдоподобности нашей модели.

Теперь заметим: ограниченность частоты колебаний зарядового разбаланса значением, равным половине частоты связующих прерываний, означает, что у связки «протон-электрон», без принятия специальных мер, половина возможного диапазона энергий связи была бы недоступна при возбуждении тем или иным способом. Это существенно ограничивало бы возможности свободного превращения энергии из одних форм в другие. Устраняющие этот недостаток специальные меры и заключаются, на наш взгляд, в устроении систем стационарных квантовых уровней у атомарных связок «протон-электрон». Так, при пребывании связки «на первом возбуждённом уровне», энергия связи равна энергии ионизации с этого уровня, а колебания зарядового разбаланса отсутствуют. При нерезонансном возбуждении, энергия которого попадает в континуум над первым возбуждённым уровнем, собственные энергии протона и электрона те же, что и на этом уровне, а энергия возбуждения, т.е. энергия колебаний зарядового разбаланса, отсчитывается с нуля, соответствующего этому уровню. Опять же, эта энергия не может превысить половину энергии ионизации с этого уровня. Чтобы была уменьшена остающаяся «мёртвая зона» энергий связи, требуется следующий стационарный уровень – и так далее. Таким образом, наша модель объясняет – по крайней мере, качественно – назначение возбуждённых стационарных уровней энергии в атоме, а также характерное сгущение этих уровней по мере их приближения к уровню ионизации.

По логике вышеизложенного, при приобретении невозбуждённой атомарной связкой «протон-электрон» кванта нерезонансного возбуждения, соответствующего континууму, скажем, между первым и вторым возбуждёнными стационарными уровнями, энергия этого кванта дробится на две формы: часть её идёт на перевод связки на первый стационарный уровень, а остаток идёт на энергию возбуждения в форме колебаний скважности зарядового разбаланса. Таким дроблением энергии легко объясняется феномен флуоресценции при облучении вещества нерезонансным ультрафиолетом – когда высвечивание происходит при «скатывании» электрона не в основное состояние, а на ближайший нижерасположенный стационарный уровень.