Более точные вычисления массы нейтрона выполнялись через энергетические балансы ядерных реакций. Так, Чедвик проанализировал реакцию испускания нейтронов бором при его бомбардировке α-частицами:

B¹¹ + He⁴ -> N¹⁴ + n¹.

При этом в энергетический баланс были включены массы всех четырёх участников, а также кинетические энергии α-частицы, атома азота и нейтрона – результирующая масса нейтрона составила 1.0067 [С1], что меньше (!) массы протона. Ещё меньшее значение, 1.0063, получили авторы [Л4], на основе анализа реакции распада на α-частицы ядер лития при бомбардировке их дейтронами:

Li⁷ + H² -> 2He⁴ + n¹ .

Максимальное же значение массы нейтрона, полученное через энергетические балансы, составило, судя по сводке результатов в [С1], 1.0090, причём доверительные интервалы у минимального и максимального значений далеко не перекрывались. Это было обусловлено, на наш взгляд, двумя методологическими ошибками. Во-первых, в энергетический баланс включались как массы частиц, так и их кинетические энергии. На наш взгляд, такой подход некорректен, поскольку кинетическая энергия не является «довеском» к массе: согласно принципу автономных превращений энергии (4.4), наличие у частицы кинетической энергии означает, что её масса уменьшена на эквивалентную величину. Учёт кинетической энергии прибавлением её к массе частицы являлся, на наш взгляд, одной из главных причин систематических расхождений между значениями масс изотопов, полученными в масс-спектроскопии и через балансы энергии ядерных превращений [Б5]. Во-вторых, не принималось в расчёт, что промежуточное или конечное ядро могло при своём формировании оказаться в возбуждённом состоянии и, соответственно, излучить γ-квант – тогда энергетический баланс был бы неполным, поскольку использовавшиеся значения масс элементов были получены для основных состояний их ядер.

Оба этих источника ошибок отсутствуют в способе нахождения массы нейтрона через измерение энергии связи дейтрона – при известных массах атома водорода и дейтерия (1.0078 и 2.0136 соответственно [Ч2]). Об энергии связи здесь можно судить, зная энергию гамма-кванта, вызывающего фотораспад дейтрона. Но и при такой методике имел место разброс результатов у разных групп авторов [Ч2,И1,С1].

Для единства измерений и вычислений в ядерной физике, требовалось уменьшить неопределённость в значении массы нейтрона. Своеобразие ситуации заключалось в том, что можно было приписать нейтрону любое значение массы, не выходившее за пределы имевшегося на то время разброса в пару масс электрона. При небольшой ошибке приписанной нейтрону массы, энергии связи ядер тоже были бы известны с соответствующими небольшими ошибками – но зато единообразно. В этом, по-видимому, и заключалась причина того, что уменьшение неопределённости массы нейтрона было осуществлено не через увеличение точности измерений, а, фактически, волевым актом, выполненным теоретиком Бете [Б6]. Он сделал расчёт массы нейтрона на основе самых достоверных, с его точки зрения, параметров и переводных коэффициентов, и привёл анализ погрешностей – однако, не пояснил, отчего разброс результатов измерений по одной и той же методике, выполненных на различных установках, на порядок превышал вычисленный им доверительный интервал. Но поскольку предложенное Бете значение, 1.00893±0.00005 [И1], обеспечивало единство измерений и вычислений на многие годы вперёд, его-то и включили в справочные издания (см., например, [Э1]) – а впоследствии, при переходе на углеродную шкалу атомных весов [К8], внесли в него соответствующую поправку.

После принятия значения, предложенного Бете, неоднократно сообщалось о согласующихся с ним результатах новых измерений энергии связи дейтрона, дававших значения около 2.22 МэВ. Эти результаты, например, Хэнсона [Х2], Белла и Эллиота [Б7], а также Мобли и Лаубенстейна [М4], принимались некритично – а ведь там имелись веские основания для сомнений [Г5]. И наш, на первый взгляд, неуместный тезис о том, что истинное значение массы нейтрона меньше принятого на одну массу электрона, на самом деле может оказаться верен.

Как же мы представляем нейтрон? Напомним, что протон (4.6) мы представляем квантовым пульсатором с нуклонной частотой, имеющим модуляцию на электронной частоте с фазой положительного заряда. Масса протона меньше массы, соответствующей нуклонной частоте, не из-за «дефекта масс»: протон не является соединением суб-частиц. Здесь уменьшение массы обусловлено всего лишь прерываниями собственных нуклонных пульсаций, согласно (4.6.1). Нейтрон же, на наш взгляд – это именно соединение, но такое соединение, состав участников которого принудительно циклически обновляется: пара «протон плюс электрон» сменяется парой «позитрон плюс антипротон», и обратно. Рис.4.10 схематически показывает «дорожки» результирующих квантовых пульсаций, с учётом их фазовых соотношений. Огибающая одной из этих дорожек задаёт положительный электрический заряд, а огибающая другой – отрицательный. Высокочастотное же заполнение, т.е. нуклонные пульсации, перебрасываются из одной огибающей в другую – с частотой, вдвое меньшей электронной. На тех периодах электронной частоты, когда нуклонные пульсации находятся в «положительной дорожке», составляющей нейтрон парой являются протон и электрон, а на тех периодах, когда нуклонные пульсации находятся в «отрицательной дорожке» - позитрон и антипротон.

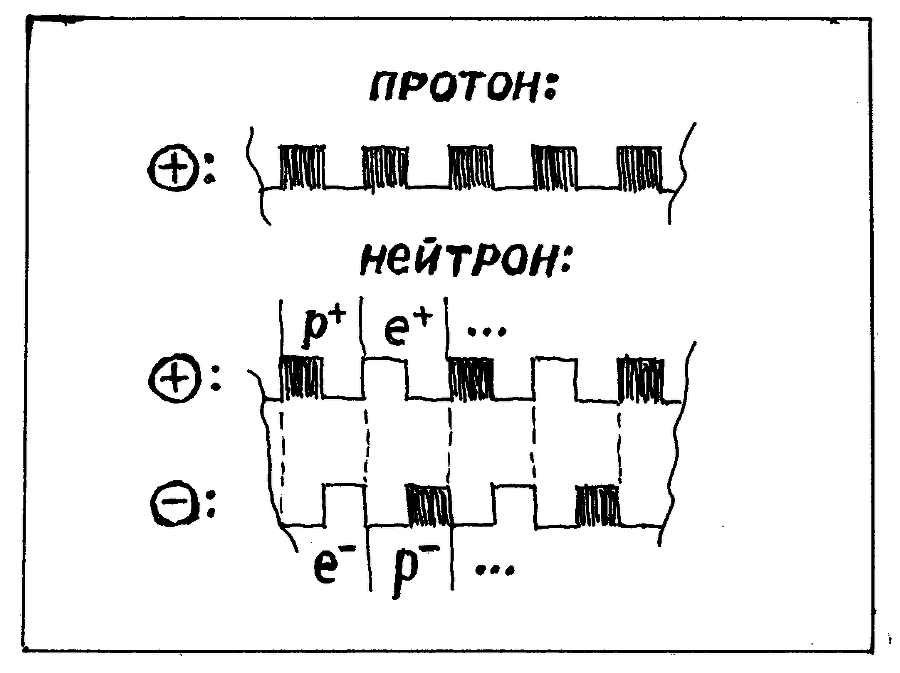
Рис.4.10

Как можно видеть, перебросы нуклонных пульсаций из одной огибающей в другую – это циклическая смена состояний, которая обладает определённой энергией. Заметим, что эта энергия появляется не за счёт уменьшения собственных энергий участников процесса: она добавляется к их собственным энергиям – отчего результирующая масса системы должна увеличиться на соответствующую величину. По логике квантовых пульсаций, энергия циклических смен двух состояний равна произведению постоянной Планка на частоту этих смен. Поскольку, в рассматриваемом случае, эта частота вдвое меньше электронной, то результирующий прирост массы, по сравнению с суммой масс протона и электрона, должен составлять половину массы электрона. Теперь заметим, что энергия циклических смен пар, составляющих нейтрон, и энергия циклических пространственных перебросов несущей между «положительным» и «отрицательным» пульсаторами – это одна и та же энергия. А поскольку энергия циклических пространственных перебросов зависит от расстояния, на которое они производятся, то два пульсатора, составляющие нейтрон, обязаны находиться на определённом расстоянии друг от друга. Таким образом мы и объясняем природу связи «на приросте масс», благодаря которой существуют нейтроны. Используя выражение (4.9.1), можно оценить расстояние, которое должно разделять центры двух пульсаторов в нейтроне: при K=700 км/с оно составляет ~2.8·10^-15 м, что неплохо соответствует характерному нуклонному масштабу.

Как можно видеть, в нейтроне всегда присутствуют единичные разноимённые заряды, которые компенсируют друг друга – потому нейтрон электрически нейтрален. Вместе с тем, эти заряды образуют электрический диполь. Этим, на наш взгляд, и объясняется загадочная способность нейтрона к слабому участию в электромагнитных взаимодействиях – отчего наблюдается, например, пространственная селекция летящих нейтронов в сильных неоднородных электрических и магнитных полях.

Подчеркнём, что связь «на приросте масс» имеет принципиальное отличие от связи «на дефекте масс»: свободный нейтрон нельзя расщепить на составляющие с помощью, например, гамма-кванта – нейтрон не может его поглотить, т.к. нейтрону «некуда» возбуждаться. Вместе с тем, энергия связи в нейтроне должна быть превращаема в другие формы энергии – согласно закону сохранения энергии. Поэтому, при распаде свободного нейтрона, энергия связи в нём должна превращаться, на наш взгляд, в энергию гамма-излучения – но никак не в энергию антинейтрино (напомним, что гипотеза о нейтрино понадобилась, чтобы спасти закон сохранения релятивистского импульса, который с очевидностью нарушался при бета-распаде (4.5)). Но, по логике вышеизложенного, даже при «приросте масс» нейтрон должен быть вполне стабильным объектом. О возможной причине распада свободных нейтронов, вылетающих из атомных котлов, мы скажем ниже (4.13).