В реакциях распада выделение энергии тоже сопровождается потерей массы. Ведь, при делении ядра кроме двух дочерних ядер должны вылетать и совсем мелкие осколки. Аналогично, если разбить кирпич ударом на половинки, то, кроме них, останутся и мелкие крошки, осколки. Так же и при отрыве капель жидкости, — кроме основной капли, в перетяжке всегда отделяется и крошечный шарик Плато (Рис. 130). Поэтому, если уж следовать капельной модели ядра, физикам следовало принять, что такая же мелкая капля-частица образуется при делении ядер. Эта частица и уносит "пропавшую" массу. В случае деления тяжёлых ядер, эта частица — нейтрон (если его реальная масса чуть выше принятой, это и породит иллюзию исчезновения массы в реакции, § 3.15). В случае α-распада таких частиц вообще не обнаружили, хотя по капельной модели ядра они тоже должны бы быть. Понятно, почему и здесь масса mтеряемой частицы соотносится с энергией распада: чем больше энергия деления E, чем мощней удар, сотрясающий и разрушающий частицу, тем массивней вылетающие осколки.
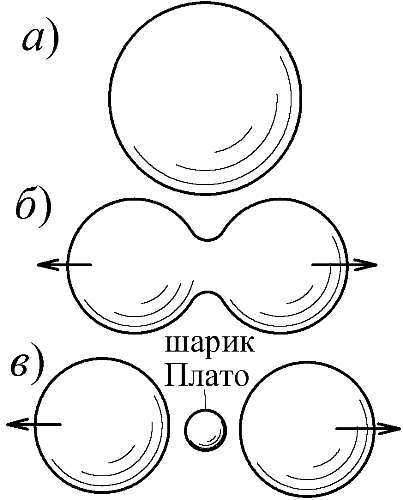
Рис. 130. Деление капель (или ядер) с образованием шарика Плато (частицы) из перетяжки [135].
Впрочем, всё это относилось к реакциям, а ядра обладают определённой массой, не зависящей от того, каким путём, — делением или синтезом, — они получены. Теряемый в реакциях вес (дефект массы) — это лишь разница масс исходных и конечных ядер. Значит, что-то задаёт устойчивую массу ядра, а, при делении или синтезе, ядро лишь сбрасывает лишнюю массу-балласт в виде частиц. Что же это за частицы? Вероятно, это упомянутые ранее гаммоны (§ 3.8). Ведь типичный дефект масс составляет около 0,04 масс протона (или кратную величину), то есть порядка 70 me, а это близко к массе гаммона в 66 me, так же бесследно исчезающей в реакциях с элементарными частицами. Почему же теряется всегда одна и та же масса, а ядра имеют стандартный вес? Ответ прост: каждое ядро состоит из определённого числа стандартных частиц, имеющих постоянную массу. И, точно, любое ядро состоит из нейтронов и протонов, однако сумма их масс никогда не равна массе образуемого ими ядра, — эту разницу и назвали "дефектом массы". По закону сохранения массы, этого не может быть, — частицы после слияния должны вместе весить столько же, сколько и до. Значит, в ядре есть и другие частицы. Действительно, мы выяснили, что ядро — это не одни голые протоны и нейтроны: в ядре эти частицы уложены, как в кульке, в бипирамидальном остове, каркасе (§ 3.3), вероятно, тоже имеющем стандартный вес, который надо учитывать. Иными словами масса ядра — это вес брутто (товар с упаковкой), а сумма масс протонов и нейтронов — это вес нетто (чистый вес, без тары).
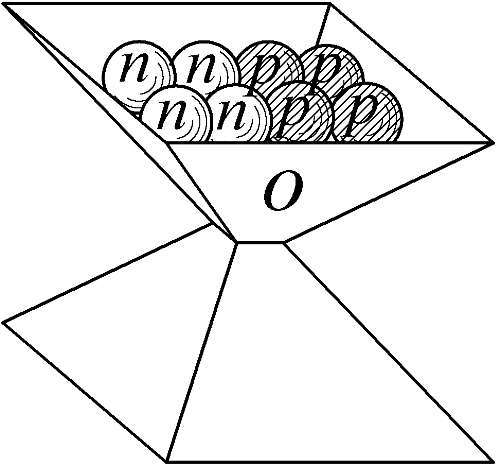
Рис. 131. Масса m ядра складывается из масс нейтронов n, остова o, протонов p, уложенных в остове, словно семечки, горошины в кульке.
В таком случае, масса ядра m=nN+o+pZ, где n— масса нейтрона, N —число нейтронов, o— масса остова (упаковки), p —масса протона, Z— число протонов (Рис. 131). Тогда масса ядра водорода H= o+p, дейтерия D= n+o+p, гелия He=2 n+o+2 p. Поэтому, сумма масс двух ядер дейтерия D, каждое из протона и нейтрона, — не равна массе ядра гелия He. Оно чуть легче: при соединении двух ядер D один остов оказывается лишним, D+D=2 n+2 o+2 p=He +o. Избыточный остов отделяется и улетает при слиянии ядер, унося массу и, — отдавая при соударениях энергию синтеза в виде тепла. Учёные же приписали этот дефект массы — переходу её в энергию, поскольку пренебрегли массой остова o, приравняв вес кулька, тары, — к нулю. Тем же вызван дефект массы у других ядер. Построенная Таблица 6 показывает, что дефект почти исчезает, если каждое ядро, кроме протонов и нейтронов, содержит ещё остов. Найденные по методу наименьших квадратов массы n, o, p, соответствуют не только массе ядер, но и найденной Чедвиком разнице масс нейтрона и протона (порядка массы гаммона), близкой к массе остова в 0,016·1822=30 me[55]. Как видим, вес голого протона p=0,992 отличается от обычно измеряемой в опытах массы ядра водорода H= o+p=1,008, поскольку в ядре протон окружён ещё остовом o=0,016. Если в ходе распада ядро лишается остова, оно его вскоре восстанавливает, поскольку в вакууме всегда носится множество мелких нейтральных частиц (октонов, гаммонов и т. п.).
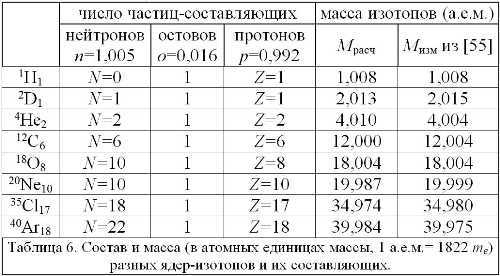
Оставшиеся малые расхождения, скажем у инертных газов, можно устранить, учтя кроме массы остова (тары) ещё и массу перегородок (упаковочного материала), словно слои пенопласта и картона, отделяющих нуклонные слои, по гипотезе Ридберга. Именно Ридберг, ставший предтечей Ритца в открытии спектральных формул атомов, предположил, что массу ядра образуют не только протоны, но и окружающие их лёгкие оболочки с весом, равным дефекту масс и находящимся в периодической зависимости от номера элемента. Ту же точку зрения развивал и Ван-ден-Брук (см. его биографию, написанную Ю.И. Лисневским, М.: Наука, 1981), впервые открывший связь номера элемента с зарядом ядра, числом протонов и допускавший существования частиц с массой, много меньшей ядра водорода, дающих при соединении с ядрами малые отклонения атомных весов от целых чисел. Эта концепция оболочек (§ 3.6) — естественно следует не только из закона сохранения массы, но также из аналогии ядерных и химических свойств. Подобно тому, как в химии давно известны комплексные и кластерные соединения, в которых центральные группы атомов окружены молекулярными оболочками стандартных масс и правильных геометрических форм-многогранников, так же и ядра, нуклоны заключены в оболочки-капсулы из стандартных частиц.
Итак, по открытому Ломоносовым закону сохранения, масса ядра (частицы) всегда равна сумме масс компонентов. Любые расхождения, особенно большие, означают, что чего-то не учли, — каких-то летучих нейтральных частиц, реальность которых вытекает из закона сохранения массы. Масса не исчезает и не возникает из энергии. Так, при рождении электрон-позитронных пар частицы, как показали опыты, не рождаются из вакуума, а выбиваются из ядер γ-лучами. Другой пример: рождение частиц в столкновениях, скажем при соударении протонов в большом адронном коллайдере. Масса mвозникших частиц соотносится с энергией столкнувшихся протонов как E=mc 2. Но это не значит, что частицы родились из энергии. Протоны, разогнанные в ускорителе до огромных скоростей, при столкновениях могут разбивать другие частицы, вырывая крупные осколки, порой тяжелее самих протонов. Ускорители подобны тяжёлой артиллерии, стреляющей снарядами-протонами по зданиям-частицам, как из кирпичиков сложенных из электронов и позитронов (§ 3.9). Чем выше энергия протона, тем больший кусок от здания другой частицы он отколет. Если все частицы состоят из связанных в кристаллы электронов и позитронов, то более энергичные протоны способны разорвать больше таких связей. Потому и масса отколотой частицы будет пропорционально больше. Поскольку энергия связи одного электрона и позитрона E 1=2 mec 2(§ 1.16), то частица из Nэлектронов потребует для своего отрыва энергии E=2 Nmec 2, но 2 Nme— это как раз масса mобразующейся частицы, равная сумме масс составляющих её электронов и позитронов. Потому масса образованной частицы и пропорциональна приложенной энергии E=mc 2.
Два сталкивающихся протона играют роль молота и наковальни. Возможно, между ними оказывается не одна крупная частица (ядро), а много мелких, типа гаммонов, собранных протонами по пути при движении в кольце ускорителя. При соударении все эти частицы сковываются воедино, как металлические заготовки на наковальне кузнеца. Чем выше энергия протонов, тем больше частиц они смогут склепать, припечатать, тем массивней возникшая частица. Итак, рождённые в столкновениях частицы это не преображённая энергия, а лишь продукт синтеза или распада от ударов.