Оно движется — оно не движется, оно далеко — оно же и близко,
Оно внутри всего — оно же вне всего[144].
Современная физика вышла за рамки таких пар противоположностей, как сила и материя, частицы и волны, движение и покой, существование и несуществование. Из них самой фундаментальной кажется последняя, но в атомной физике мы должны подняться и над ней. Это та сторона квантовой теории, которую сложнее всего осознать, и именно она становится причиной споров об интерпретации этой теории. При этом один из самых удивительных аспектов мистических учений Востока заключается в том, что они тоже поднимаются выше понятий существования и несуществования и часто подчеркивают это немаловажное обстоятельство. Вот что утверждает Ашвагхоша.
«Таковость»… и не становится, и не прекращает становиться… Таковость не присутствует ни в каком месте, ни в каком пункте… не возникает ни от двойственного, ни от недвойственного… Таковость ни чиста, ни нечиста… Таковость не возникает и не приходит к концу[145].
Сталкиваясь с действительностью за рамками противоположностей, физики и мистики должны выработать особый образ мышления, не скованный узкими рамками классической логики, но подвижный и способный менять точку зрения. Так, в атомной физике мы уже привыкли применять в описании материи и концепцию волн, и концепцию частиц. Мы научились чередовать два этих представления, переключаясь между ними, чтобы адекватно истолковывать явления в мире атома. Именно так мыслят восточные мистики, когда пытаются толковать свое восприятие реальности за рамками противоположностей. Вот что сказал Лама Говинда.
Восточный образ мышления более склонен к кружению вокруг объекта созерцания… многостороннему, т. е. многомерному восприятию, создаваемому путем наложения отдельных картин, полученных из разных точек зрения[146].
Чтобы понять, как в атомной физике можно переключаться между концепциями частиц и волн, рассмотрим понятие волны и частицы подробнее. Волна — модель колебаний в пространстве и времени. Рассматривая ее на определенном отрезке времени, мы увидим систематический пространственный шаблон (рис. 16). Характеристики этого шаблона — амплитуда А и длина волны L, расстояние между двумя соседними гребнями.
Рис. 16. Волновые колебания
Можно изучать и другие характеристики волны, например движение определенной точки. Тогда мы увидим колебания определенной частоты (она определяется числом целых колебаний за секунду). Представим себе частицу. По классическим представлениям, она в любой момент имеет вполне определенное местоположение, а ее состояние движения может быть описано в терминах скорости и энергии.
Частицы, двигающиеся с высокой скоростью, обладают высокой энергией. Физики для описания движения частицы редко пользуются категорией «скорость», заменяя ее величиной, которая называется «импульс» и равна произведению массы частицы на ее скорость.
Итак, квантовая теория связывает свойства вероятностной волны со свойствами соответствующей частицы, а амплитуду волны в определенной точке — с вероятностью существования частицы в ней. Если амплитуда вероятностной волны большая, то велика вероятность того, что в этой точке мы найдем частицу. Там, где амплитуда вероятностной волны невелика, найти частицу маловероятно. Амплитуда волны, изображенной на рис. 16, одинакова на всем ее протяжении, поэтому частица может с равной вероятностью находиться в любой точке волны[147].
Движение частицы может быть охарактеризовано частотой и длиной волны. Последняя обратно пропорциональна импульсу частицы: волна меньшей длины соответствует частице, имеющей больший импульс (а следовательно, при равной массе, и большую скорость). Частота волны прямо пропорциональна импульсу частицы. Так, фиолетовый свет характеризуется высокой частотой и малой длиной волны, состоит из фотонов с высокой энергией и высоким импульсом. А красный характеризуется низкой частотой и большой длиной волны, его фотоны обладают низкой энергией и небольшим импульсом.
Волна, распространяющаяся в пространстве, как в нашем примере, немного сообщает нам о местонахождении соответствующей частицы. С одинаковой вероятностью она может быть обнаружена в любой точке. Но очень часто местонахождение частиц приблизительно известно, как, например, при описании электрона внутри атома. Тогда вероятность существования частицы в разных точках должна быть ограничена определенной областью атома. За ее пределами вероятность равна нулю. Этого можно достичь при условии существования волны, представленной на рис. 17. Здесь вероятность существования частицы ограничена областью Х. Такие модели называются волновыми пакетами[148]. Это совокупность волн с разными длинами. Интерферируя, они взаимокомпенсируют друг друга за пределами области Х, и амплитуда волны, а следовательно, и вероятность обнаружить там частицу равна нулю. Волны внутри области Х показывают, что частица находится где-то в ней, но не позволяют определить ее местонахождение точно. Мы можем только подсчитать вероятность нахождения частицы для каждой точки X. (Скорее всего, она где-то в середине, так как там амплитуда выше всего; менее вероятно, что частица расположена у края волнового пакета, поскольку там амплитуда колебаний мала.) Следовательно, размер волнового пакета — показатель неопределенности местонахождения частицы.
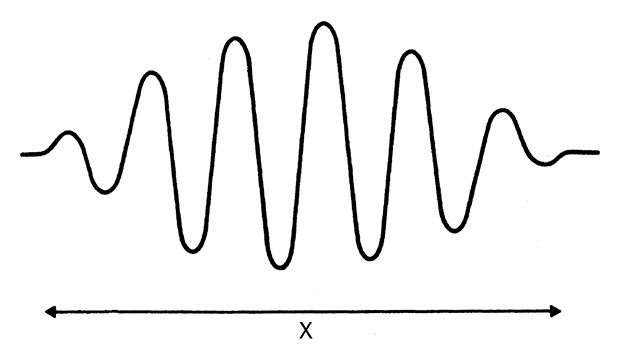
Рис. 17. Волновой пакет, соответствующий положению частицы в зоне Х
Важное свойство таких волновых пакетов заключается в том, что они не имеют определенной длины волны: расстояние между соседними гребнями неодинаково на протяжении паттерна. Есть определенный разброс по длинам волн, величина которого зависит от длины пакета: чем короче пакет, тем он значительнее. Это не имеет никакого отношения к квантовой теории, это следствие свойств обычных волн. Пакеты не имеют характерной длины волны. Квантовая теория начинает действовать, когда мы связываем длину волны с импульсом соответствующей частицы. Если пакет не имеет определенной длины волны, частица не имеет определенного импульса. Неопределенным будет не только ее точное местонахождение, но и ее импульс (это вызвано разбросом в длине волн). Две эти неопределенности связаны друг с другом, поскольку разброс длины волн (неопределенность импульса) зависит от длины волнового пакета (неопределенности местонахождения). Если мы хотим точнее определить местонахождение частицы (сократить длину волнового пакета), увеличится разброс длины волн, а следовательно, и неопределенность относительно импульса частицы.
Точная математическая формула взаимосвязи между неопределенностями местонахождения и импульсом частицы известна как принцип неопределенности Гейзенберга. Он подразумевает, что в субатомном мире мы не можем одновременно получить точные данные о положении и импульсе любой частицы. Чем лучше нам известно ее положение, тем менее точно мы можем определить ее импульс, и наоборот. Можно попытаться точно измерить одну из этих квантовых наблюдаемых, но при этом ничего не узнать о второй. Важно понимать, что это ограничение принципиально, оно не объясняется несовершенством наших измерительных приборов.
Взаимосвязь между неопределенностью координаты и импульса частицы — не единственное проявление принципа неопределенности. Похожие соотношения бывают между другими величинами — например, временем, в течение которого происходит какое-то явление на атомарном уровне, и количеством энергии, задействуемой при этом. Это очевидно, если мы рассматриваем волновой пакет не как пространственную модель, а как колебания во времени. Когда частица проходит мимо определенной точки, колебания волн в ней начинаются с небольшой амплитуды, которая сначала увеличивается, а затем уменьшается до полного затухания. Время, необходимое для этого, соответствует промежутку, в течение которого частица проходит мимо точки наблюдения. Мы можем сказать, что прохождение частицы состоялось, именно в это время, но точнее определить момент мы не способны. Поэтому продолжительность колебаний соответствует неопределенности локализации события во времени.