Линии иного вида носят другие названия. Те не прямые линии, которые составлены из отрезков прямой (черт. 1), называются л о м а н ы м и. Все прочие линии – не прямые и не ломаные – называются кривыми (черт. 2).
Прямые линии чертят на бумаге, пользуясь линейкой.
Через одну точку можно провести сколько угодно прямых линий. Но через д в е точки сразу может проходить не более о д н о й прямой: нельзя через две точки провести больше одной прямой так, чтобы проведенные линии не сливались в одну. Этим свойством прямых линий пользуются для перекалывания узоров, составленных из прямых линий. Предположим, что вы желаете изобразить в точности узор черт. 3a, т. е. желаете, как говорят, «снять с него копию». Вы можете поступить так: подложить под узор чистую бумагу и проколоть иглой (или ножкой циркуля) конечные точки всех его линий. У вас получится на чистой бумаге то, что. вы видите на черт. 3b. Если затем, глядя на узор; вы соедините точки черт. 3b по линейке прямыми линиями – у вас получится точная копия узора; так как между двумя точками можно провести только одну прямую линию, то ясно, что отрезки, соединяющие точки черт. 3b, должны быть те самые, что и на черт. 3a.
На классной доске мы можем чертить прямые линии помощью шнура, натертого мелом. Натянув его между теми двумя точками, через которые мы желаем провести прямую, приподнимают немного шнур посредине и отпускают: шнур отпечатывает на доске свою форму, т. е. прямую линию. Это называется «отбить» прямую. Плотники, отбивая прямые на бревнах, брусьях или досках, натирают шнур не мелом, а углем.
Чтобы обозначить прямую линию на поле, на лугу, в лесу, вообще, как говорят, «на местности», ее не прочерчивают на земле, а втыкают лишь на ее концах по шесту («вехе»): этого достаточно, потому что через две точки (вехи) может проходить только одна прямая.
Чтобы не указывать на чертеже пальцем, о каком отрезке идет речь, ставят у его концов буквы; желая указать этот отрезок, называют буквы, стоящие у его конечных точек; этого достаточно, потому что через две точки может проходить только одна прямая. Левый стоячий отрезок на черт. 4, например, надо называть АО, нижний лежачий – DС, и т. д. Для таких dобозначений принято упо треблять п р о п и с н ы е буквы латинского алфавита.
Другой способ обозначения отрезков состоит в том, что возле их середины ставят одну малую букву. Например, прямую АВ можно назвать просто b, a AD – а, и т. п.
Называя л о м а н у ю линию, надо перечислить по порядку буквы, поставленные у концов всех ее отрез ков. Например, говорят «ломаная ABCOD» (найдите ее на черт. 4).
Буквы для обозначения точек и линий принято в математике употреблять не русские, а латинские. Они не слишком отличаются от русских, поэтому к употреблению их легко привыкнуть.
Повторительные вопросы
Начертите несколько прямых, ломаных и кривых линий. – Сколько прямых может проходить через одну точку? А через две? – Во скольких местах могут пересекаться две прямые? – Как перекалывают узоры? – Как «отбивают» прямые линии? – Как отмечают их на местности? – Как обозначают прямые линии буквами? Как обозначают ломаные линии? – Когда употребляют прописные буквы и когда – малые?
§ 2. Масштаб
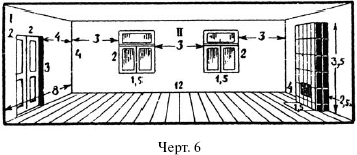
Изображение участка земли, пола комнаты или квартиры в уменьшенном виде называется планом этого участка, комнаты или квартиры. При этом необходимо изготовить уменьшенное изображение так, чтобы по плану участка или комнаты легко было узнать их настоящие размеры. Проще всего возле каждого отрезка на плане надписать его истинную длину. Часто так и делают, – например, когда зарисовывают план от руки, вчерне. На черт. 5 мы видим подобный план комнаты, изображенной на черт. 6. Но не всегда это бывает удобно. Обычно на плане приходится показывать много подробностей, – например, не только размеры самой комнаты, но и ширину окон, дверей, стен, печи и т. п. Если все эти размеры надписать на плане, в нем трудно будет разобраться.
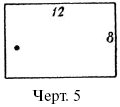
Чтобы план был ясен и нагляден, его изображают «в масштабе». Это значит, что взамен метра действительно длины чертят на плане определенный небольшой отрезок, – напр. 1/2 см; тогда длина комнаты (черт. 6) 12 м изобразится на плане отрезком в 6 см; ширина ее 8 м – отрезком в 4 см; ширина окна 1,5 м – отрезком 0,75 см, или 7,5 мм и т. д. (черт. 7). И наоборот, если на плане ширина дверей равна 1 см, то это показывает, что настоящая ее ширина – 2 метра. О таком плане говорят, что он начерчен в масштабе «2 метра в 1 см».
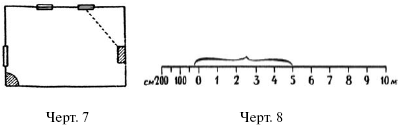
К планам, начерченным в масштабе, обычно прилагают так называемый «линейный масштаб», который служит для того, чтобы по длине отрезков на плане удобно было находить их истинную длину. Образец такого масштаба изображен на черт. 8. Пользуются им следующим образом. Предположим, мы желаем узнать, как велико истинное расстояние от середины правого угла комнаты до ближайшего угла печки; оно показано на плане черт. 7 точечной линией (пунк тиром). Раздвинув ножки циркуля на расстояние, равное этому отрезку, переносим взятое расстояние на линейный масштаб (черт. 8) так, чтобы правое острие циркуля было у одной из отметок целых метров (т. е. направо от нуля) а левое острие – налево от нуля. В нашем случае правое острие окажется у отметки «5 метров», левое – у отметки «25 см» (число 25 на масштабе не написано, но подразумевается). Значит, истинное расстояние от окна до печки – 5 м 25 см.
Зная, скольким метрам истинной длины отвечает каждый сантиметр плана, легко рассчитать, во сколько раз расстояния на, плане меньше их настоящей величины. В нашем случае расстояния плана меньше их истинной («натуральной») величины во столько раз, во сколько 1 см меньше 2 метров, т. е. в 200. Другими словами, план выполнен в 1/200 натуральной величины. Дробь 1/200 называется «численным масштабом» плана. Если бы он был начерчен в масштабе «1 м в 1 см», то ч и с л е н н ы й масштаб плана был бы 1/100. Масштабу «1/2 м в 1 см» отвечает численный масштаб 1/50 и т. п.
Повторительные вопросы
Что называется планом? – Что значит «начертить план в масштабе»? – В каком масштабе выполнен план черт. 7? В какую долю натуральной величины? – Каким численным масштабам соответствуют следующие: «1 м в 1 см», «2 м в 1 см», «0,5 м в 1 см»?
§ 3. Диаграммы
Масштабом пользуются не только для черчения планов, но и для того, чтобы наглядно изображать соотношения различных длин. Пусть, например, вы узнали, что огромный ящер, «динозавр», когда-то живший на земле, имел в высоту 12 метров. Мы желаем наглядно сопоставить рост этого вымершего чудовища с ростом среднего человека (1,7 м). Для этого начертим отрезок (черт. 9), изображающий рост динозавра в каком-нибудь масштабе, например, 2 м в 1 см, – а рядом с ним другой отрезок, изображающий в том же масштабе рост человека. Первый отрезок будет иметь в длину 6 см, второй – только 8,5 мм. Глядя на такой чертеж (черт, 9), мы, конечно, гораздо яснее представляем себе огромный рост динозавра, чем обдумывая число 12 метров.
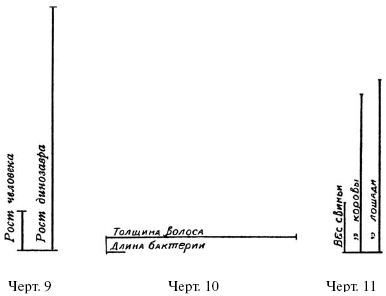
Если пожелаем сравнить рост динозавра также с ростом средней лошади (2 м) и с ростом жирафа (5,5 м), то должны будем рядом с сейчас начерченными двумя прямыми начертить еще две: одну – длиною в 1 см – для лошади, и другую – длиною 2,8 см – для жирафа. (Сделайте это в вашей тетради.) То, что мы начертили, есть «диаграмма» роста животных.