За период 1891–1977 разыграно 204 медали чемпионов мира, в том числе 67 среди мужчин, 57 среди женщин, 55 в парном катании, 25 в спортивных танцах; 174 золотые медали европейских первенств – соответственно: 68, 41, 41, 24.

  Наибольших успехов в международных соревнованиях добились Г. Графстрём (олимпийский чемпион 1920, 1924, 1928, Швеция), У. Сальхов (10 раз чемпион мира, 9 – Европы, в 1901–11, Швеция), Соня Хени (10 – мира, 6 – Европы, 3 – Олимпийских игр, в 1927–36, Норвегия), И. К. Роднина (9 – мира и Европы, 2 – Олимпийских игр, в 1969–72 в паре с А. Н. Улановым, в 1973–77 с А. Г. Зайцевым, СССР), Л. Е. Белоусова и О. А. Протопопов (4 – мира и Европы, 2 – Олимпийских игр, в 1964–68, СССР), в спортивных танцах Л. А. Пахомова и А. Г. Горшков (6 – мира и Европы, 1 – Олимпийских игр, в 1970–76, СССР).

  Среди чемпионов и призёров чемпионатов мира, Европы и Олимпийских игр: женщины – К. Хейс, П. Флеминг, Д. Линн, Д. Хэмилл (США), Г. Зайферт и К. Эррат (ГДР), Ш. Дейкстра (Нидерланды); мужчины – Р. Баттон, Д. и А. Дженкинсы, Т. Вуд (США), Д. Джексон (Канада), Э. Данцер и В. Шварц (Австрия), О. Непела (ЧССР), Дж. Карри (Великобритания), Я. Хофман (ГДР), С. Н. Волков, В. Н. Ковалев, С. А. Четверухин (СССР); спортивной пары – Б. Вагнер и Р. Поул (Канада), М. Килиус и Г. Боймлер (ФРГ), Р. Кермер и Р. Эстеррайх (ГДР), Н. А. и С. А. Жук, Т. А. Жук и А. Ю. Горелик, Л. С. Смирнова и А. А. Сурайкин (СССР); спортивные танцы – Е. Романова и П. Роман (ЧССР), Д. Вествуд и Л. Демми, Д. Денни и К. Джонс, Д. Таулер и Б. Форд (Великобритания), И. В. Моисеева и А. О. Миненков, Н. В. Линичук и Г. М. Карпоносов (СССР) и др.

  Советские фигуристы завоевали на Олимпийских играх 5 золотых и 5 серебряных медалей, на чемпионатах мира – 20 золотых, 17 серебряных и 9 бронзовых, на чемпионатах Европы – соответственно: 18, 18 и 13. 17 сов. фигуристам присвоено звание заслуженного мастера спорта, 32 – мастера спорта СССР междунар. класса. Лучшие школы Ф. к. в Москве и Ленинграде, где работают засл. тренеры СССР Т. А. Толмачева, С. А. Жук, Е. А. Чайковская, В. Н. Кудрявцев, Т. А. Тарасова, И. Б. Москвин, засл. тренеры РСФСР Т. Н. Москвина, А. Н. Мишин и др.

  Лит.: Панин Н. А., Искусство фигуриста, М., 1956; Рыжкин В. И., Ледовая сюита, М., 1975; Фигурное катание на коньках, под ред. А. Б. Гандельсмана, М., 1975.

  В. И. Рыжкин.

Фигурное катание. Чемпионы мира: Г. Зайферт (ГДР).

Фигурное катание. Чемпионы мира: И. К. Роднина и А. Г. Зайцев (СССР).

Фигурное катание. Чемпионы мира: И. В. Моисеева и А. О. Миненков (СССР).

Фигурное катание. Чемпионы мира: Эррат (ГДР).

Фигурное катание. Чемпионы мира: Э. Данцер (Австрия).

Фигурное катание. Чемпионы мира: Л. Е. Белоусова и О. А. Протопопов (СССР).

Фигурное катание. Чемпионы мира: Д. Таулер и Б. Форд (Великобритания).

Фигурное катание. Чемпионы мира: Н. Ковалёв (СССР).

Фигурное катание. Чемпионы мира: П. Флеминг (США).

Фигурное катание. Чемпионы мира: Д. Хэмилл (США).

Фигурное катание. Чемпионы мира: С. Н. Волков (СССР).

Фигурное катание. Чемпионы мира: Д. Денни и К. Джонс (Великобритания).

Фигурное катание. Чемпионы мира: Л. А. Пахомова и А. Г. Горшков (СССР).

Фигурное катание. Чемпионы мира: О. Непела (ЧССР).

Фигуры равновесия

Фигу'ры равнове'сия, геометрической конфигурации, которые может принять жидкая масса, находясь в положении относительного равновесия (под относительным равновесием обычно понимают установившееся движение жидкости, при котором вся масса жидкости движется таким образом, что расстояния между её частицами остаются постоянными). Рассматривают движение жидкости либо только в собственном гравитационном поле, либо под действием этого поля и, сверх того, притяжения др. внешних тел. В теории Ф. р. изучаются две основные, тесно связанные между собой проблемы: существование тех или иных Ф. р. вращающихся жидкостей и устойчивость Ф. р., подверженных влиянию малых возмущений.

  Теория Ф. р. зародилась в 17 в., однако и во 2-й половины 20 в. она далека от своего завершения. Наиболее полные результаты принадлежат А. М. Ляпунову , который впервые построил точную математическую теорию Ф. р. вращающейся жидкости (однородной и неоднородной) и получил ряд результатов в теории устойчивости простейших Ф. р. (т. н. эллипсоидов Маклорена и Якоби), и А. Пуанкаре , доказавшему, в частности, что относительное равновесие однородной жидкости возможно только в том случае, когда угловая скорость вращения (меньше величины

, где f – постоянная тяготения, r – плотность жидкости,  – т. н. предел Пуанкаре. Если на однородную несжимаемую покоящуюся жидкую массу не действуют никакие внешние силы, то её единственной Ф. р. является сфера. Ф. р. однородной жидкости во всех случаях симметричны относительно плоскости, проходящей через её центр инерции перпендикулярно оси вращения, а всякая прямая, параллельная оси вращения, пересекает поверхность жидкости не более чем в двух точках. Наиболее изученными Ф. р. однородной несжимаемой вращающейся жидкости являются эллипсоидальные Ф. р.: эллипсоиды вращения и трёхосные эллипсоиды. Эти Ф. р. образуют семейства поверхностей (линейные серии), непрерывно зависящие от величины угловой скорости w, изменяющейся между нулём и величиной, меньшей . 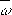Эллипсоидальные Ф. р. математически описываются алгебраическими поверхностями 2-го порядка. Приближённое решение проблемы существования Ф. р., описываемых алгебраическими поверхностями более высокого порядка, дал Пуанкаре, а строгое решение – Ляпунов, доказавший, что существуют Ф. р., близкие к эллипсоидальным, описываемые алгебраическими поверхностями порядка, большего 2. Т. о. была решена задача об устойчивости эллипсоидальных фигур при малых деформациях конфигурации.

  Большое прикладное значение имеет теория Ф. р. жидкости, испытывающей притяжение внешних сил. В статической модели, когда покоящаяся жидкость притягивается достаточно удалённой материальной точкой, доказано существование вытянутых в направлении притягивающей точки эллипсоидальных Ф. р. (приливных эллипсоидов). Наибольшие приложения в астрономии получила проблема Роша и её обобщения, устанавливающая существование эллипсоидальных (или близких к ним) Ф. р. однородной вращающейся жидкой массы, которая притягивается материальной точкой, совершающей круговые движения около центра масс жидкости с той же угловой скоростью. Эти механические модели положены в основу теории приливной эволюции, теории форм звёзд, составляющих двойную систему, теории фигур планет. Приближённая теория устойчивости Ф. р. небесных тел разработана Дж. Дарвином и Дж. Джинсом .