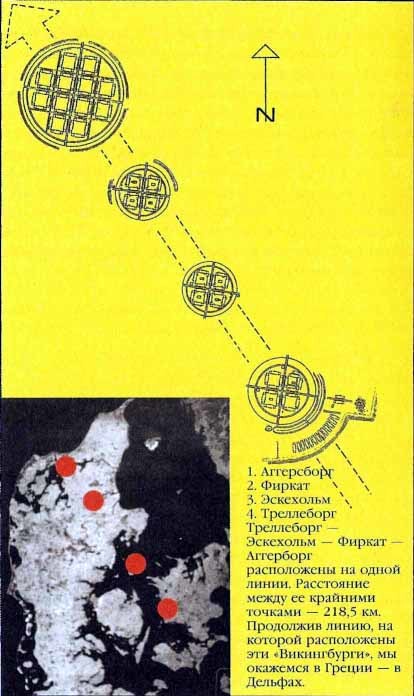
«Нельзя считать простым совпадением, что столь мощные кольцевые крепости расположены строго по одной линии. Мало того, все четыре сориентированы по оси симметрии, проходящей через параболу Треллеборга. Эти объекты были возведены кем-то, кому было весьма важно, чтобы они находились на одной линии, и кто, кроме того, располагал достаточными техническими средствами для того, чтобы возвести их таким образом на отрезке длиной свыше 200 км. Эта транспортная линия, известная с незапамятных времен, пролегает независимо от рельефа местности, будь то море, острова или материк».
Мой знакомый — тот самый, который постоянно стремится объяснить все «естественными причинами» — полагает, что все эти объекты расположили на одной линии именно викинги. А кто же еще?! Мне сразу же вспоминаются их боги: великий Один, грозный Вотан, могучий Гор! Для меня всегда настоящее мучение общаться с приверженцами столь косных взглядов. Вы считаете, что это — не наука? Не желаете видеть совершенно очевидных вещей? Прямая линия, опоясывающая шар, называется его окружностью. Это — кратчайший путь от точки до точки на криволинейной поверхности земли. Именно такую линию и обнаружил Ханссон. Еще аргументы? А помните, как сказал бог еще 2500 лет назад устами пророка Иезекииля:
«У них есть глаза, чтобы видеть, а не видят; у них есть уши, чтобы слышать, а не слышат…»
Иезекииль 12:2.
Невозможное возможно
Доисторический авиамаршрут, открытый Пребеном Ханссоном, ведет прямехонько в Дельфы — эту резиденцию древнейшего оракула в Греции. В этой связи мы можем предположить, что практически все культовые святилища Древней Греции, восходящие к доисторической эпохе, должны быть расположены на одинаковом расстоянии друг от друга. Слишком дерзкое предположение? Ничуть не бывало. Возьмите подробную карту Греции и линейку Или циркуль, с помощью которых можно будет отмерить золотое сечение.
А теперь давайте ВСПОМНИМ:
«Если прямая А-В поделена точкой Е таким образом, что вся она в целом относится к большей из получившихся частей так же, как эта большая часть к меньшей, то это означает, что через точку Е проходит золотое сечение прямой А-В. Если же взять прямую, поделенную золотым сечением, и прибавить к ней больший из отрезков, то полученная новая прямая будет поделена золотым сечением, проходящим через конечную точку первоначальной прямой. Это относится и ко всем последующим продолжениям прямой»
(Эдвальд Гретер «Теория планиметрии»).
А теперь — несколько примеров древнегреческих памятников:
— Расстояние между Дельфами и Эпидавром соответствует большему отрезку золотого сечения расстояния между Эпидавром и Делосом, то есть 62 %.
— Расстояние между Олимпией и Халкисом (Халки-дики) соответствует большему отрезку золотого сечения расстояния между Олимпией и Делосом, то есть 62 %.
— Расстояние между Дельфами и Фивами соответствует большему отрезку золотого сечения расстояния между Дельфами и Афинами, то есть 62 %.
— Расстояние между Эпидавром и Спартой соответствует большему отрезку золотого сечения расстояния между Эпидавром и Олимпией, то есть 62 %.
— Расстояние между Делосом и Элевзином соответствует большему отрезку золотого сечения расстояния между Делосом и Дельфами, то есть 62 %.
— Расстояние между Кноссом и Делосом соответствует большему отрезку золотого сечения расстояния между Кноссом и Халкисом, то есть 62 %.
— Расстояние между Дельфами и Додонами соответствует большему отрезку золотого сечения расстояния между Дельфами и Афинами, то есть 62 %.
— Расстояние между Дельфами и Олимпией соответствует большему отрезку золотого сечения расстояния между Олимпией и Халкисом, то есть 62 %.
Тот, кто даже после столь неопровержимых доказательств сомневается в том, следует ли расположение этих пунктов геометрическому плану или является случайным совпадением, видимо, никак не может сбросить с плеч давно изношенное рубище устарелых представлений. Но если бы мотивы возведения этих объектов исчерпывались лишь геометрическими принципами, это еще не казалось бы столь явным «чудом», ибо в Древней Греции работал один из величайших математиков всех времен и народов — знаменитый Евклид. В конце IV в. до н. э. он учился в Александрийском «университете», а впоследствии создал 15 основных трудов, охватывающих практически весь спектр тогдашней математики и геометрии. Евклид был современником знаменитого философа Платона, который даже слушал лекции Евклида. Известно, что Платон был не только философом, но и политиком… Остальное лежит, что называется, на поверхности: Платону при определении плана строительных работ могло принадлежать далеко не последнее слово, и благодаря его обстоятельным познаниям в геометрии Евклида культовые святилища и были расположены не произвольно, а следуя стройной геометрической системе.
Это предположение, являющее собой настоящий якорь спасения для «вечно вчерашних» ретроградов, следует отвергнуть потому, что все эти древние культовые святилища существовали еще задолго до Евклида, а время их возведения уже в эпоху классической античности, то есть собственно Древней Греции, принято было относить к незапамятным временам. Вполне возможно, что Евклид всего лишь воспользовался куда большими знаниями, позаимствовав их из неких не сохранившихся древних источников, ибо Платон, слушавший, кстати сказать, лекции Евклида, в 7 и 8-й главах своего прославленного и таинственного диалога «Тимей» упоминает о целом ряде геометрических знаний. Философ отлично понимал, что значение этих знаний выходит далеко за рамки самой Греции, и заявлял: «Пусть никто не пренебрегает геометрией. Геометрия — это знание о вечном бытии».
Советы Аполлона
А теперь давайте вспомним: древний авиамаршрут, открытый Пребеном Ханссоном, проходя через «Викингбурги» на территории Дании, нанизанные на него, словно жемчужины на нить, ведет прямо в Грецию — в знаменитые Дельфы. Там некогда пребывал легендарный «оракул». Но с какой стати это место стало считаться оракулом? Что в Дельфах такого особенного, располагающего к «оракульствованию»? Почему этот пункт, затерянный на карте мира, уже в древнейшие времена приобрел поистине всемирную известность?
Дело в том, что Дельфы еще в эпоху классической Древней Греции считались центром Вселенной. Там в древности стоял зримый знак — «пуп мира», так называемый омфалос, прекрасно обработанная глыба мрамора, украшенная скульптурами и увенчанная двумя золотыми орлами. В этих орлах древние видели посланников Зевса — отца Олимпийских богов. Однако — любопытная деталь! — Дельфы были посвящены Аполлону, который считался не только сыном Зевса, но и богом света и «пророчеств». Кроме того, Аполлону поклонялись и как великому целителю, а одним из его сыновей был не кто иной, как Асклепий, которого и сегодня называют «праотцем» врачей.
Аполлон обладал поистине безграничным могуществом и был единственным из богов, которого побаивался даже его собственный отец — Зевс. Он часто поддерживал троянцев во время сражений и — прямо с небес — брал героев под свою защиту. Самое известное прозвище Аполлона — Ликей, то есть бог света. Но самое удивительное заключается в том, что греки и сами не знали, откуда к ним пришел Аполлон. Даже в наши дни светила академической науки и знатоки мифологии ломают копья в спорах о том, пришел ли солнечный бог в Грецию с Севера или с Востока. Однако все единодушно признают тот факт, что Аполлон каждый год на несколько недель или месяц с небольшим отправлялся в гости к некоему загадочному народу, так называемым гипербореям, которые жили «по ту сторону северного ветра».
Что ж, ничего страшного. Это тоже вполне биографические данные, хотя они и почерпнуты из области мифологии. Аполлон — сын «небожителя», бог света, наконец, бог врачевания. Он поддерживал своих друзей в бою, охранял транспортные дороги, но каждый год отправлялся погостить у некоего народа, жившего «по ту сторону северного ветра». В качестве своей резиденции он выбрал Дельфы… Ну, как, все ясно?