Все эти рассуждения основаны на предположении, что студенты и больницы представляют списки, отражающие их истинные предпочтения. В этом отношении НПРИ, в сущности, исходит из того, что дезинформация по поводу предпочтений не приносит каких-либо выгод. Действительно, ни один студент и ни одна больница не могут что-либо выгадать, неправильно указав свой первый выбор. Однако для отдельного студента истинное от начала и до конца перечисление своих предпочтений, независимо от рейтингов, составляемых больницами, и от списков, представляемых другими студентами, не является оптимальным решением. Аналогично больница, имеющая более одной вакансии, поступит не лучшим для себя образом, если станет представлять правдивые списки вне зависимости от списков, представляемых студентами и другими больницами.

Пример успешной стратегической дезинформации. Чтобы убедиться в теоретической возможности выгодной дезинформации, рассмотрим пример – на редкость простой по сравнению с реальной ситуацией, с которой сталкиваются на практике студенты[29].

Предположим, что мы имеем дело с тремя студентами: Элис, Барбарой и Чарли – и тремя больницами: имени Гопкинса, Стэнфордского университета и Йельского университета. Каждой больнице требуется только один студент, и поэтому в силу изложенных выше причин у них нет оснований для искажения своих предпочтений. Исходные рейтинги представлены в табл. 2.1.

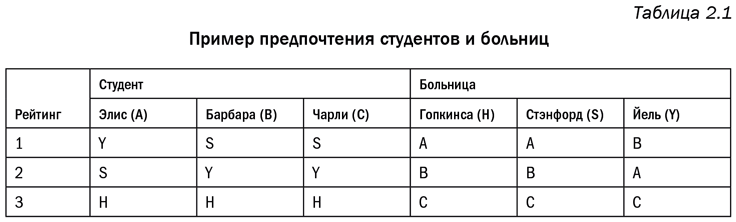
В первом раунде больницы Гопкинса и Стэнфорда предлагают свои вакансии Элис – наиболее предпочтительной для них студентке, а Йель – своей фаворитке Барбаре. Элис условно направляется в Стэнфорд, которому она отдает предпочтение перед больницей Гопкинса, а Барбара условно направляется в Йель. Таким образом, и Элис, и Барбара исключаются из списка больницы Гопкинса и на первое место в нем выходит Чарли (автоматически, поскольку кроме него в списке никого не осталось). В следующем раунде Стэнфорд и Йель повторяют свои предложения соответственно Элис и Барбаре, поскольку и та и другая занимают первые места в списках соответствующих больниц, а больница Гопкинса делает предложение Чарли. Все студенты распределены по больницам, и это распределение теперь может быть оглашено. Элис и Барбара в конечном счете очутились в больницах, которые они поставили на второе место, зато две эти больницы получили первые номера из своих списков.

Предположим теперь, что Барбара искажает свои предпочтения и представляет список, в котором на первом месте по-прежнему Стэнфорд, однако за ним на втором месте стоит больница Гопкинса, а не Йель. В этом случае проследить алгоритм работы осуществляющего распределение компьютера значительно сложнее (и возможно, читатель предпочтет пропустить следующие два абзаца, в которых дается описание этого процесса), однако оказывается, что эта дезинформация пойдет на пользу Барбаре. В конце концов она распределяется в Стэнфорд, в больницу, которую она поставила на первое место.

В первом раунде Элис вновь условно распределяется в Стэнфорд, а Барбара – в Йель. Однако теперь, поскольку Барбара утверждает, что Йель для нее занимает третье место по предпочтительности, ее имя не исключается из списка больницы Гопкинса. Из этого списка, однако, по-прежнему, исключается Элис, и теперь на первом месте в нем стоит Барбара, а на втором – Чарли. В следующем раунде больница Гопкинса и Йель сделают предложения Барбаре, ставшей теперь их фавориткой, а Стэнфорд повторяет свое предложение Элис. Барбара утверждает, что больница Гопкинса больше подходит ей, чем Йель; поэтому ее условное распределение в Йель аннулируется и она временно закрепляется за больницей Гопкинса. В результате она исключается из списка больницы Гопкинса. Скорректированные рейтинги больниц перед началом третьего раунда приводятся в табл. 2.2.

На третьем этапе каждая больница вновь делает предложение студенту, занимающему первое место в ее скорректированном рейтинге: больница Гопкинса – Барбаре, а Стэнфорд и Йель – Элис. Условное распределение, формируемое компьютером, снова направляет Барбару в больницу Гопкинса, но Элис попадает в Йель, который в ее списке значился под первым номером. В результате Элис исключается из списка Стэнфорда, и на первое место в нем выходит Барбара. На четвертом этапе Барбара получает предложение и от больницы Гопкинса, и от Стэнфорда, в то время как Элис опять выбрана Йелем. Теперь компьютер направляет Барбару в Стэнфорд (первый номер в ее списке) и исключает ее из списка больницы Гопкинса. Далее, в пятом раунде компьютер направляет Элис в Йель, Барбару в Стэнфорд, а Чарли в больницу Гопкинса. Это распределение и подлежит официальному оглашению.

Дезинформация Барбары позволила ей попасть в больницу, стоявшую в ее списке на первом, а не на втором месте, как это было бы, если бы она действовала честно. (Получилось так, что благодаря ее нечестности Элис попала в первую в ее системе больницу, а не во вторую.) Занизив рейтинг больницы, которая ставила ее на первое место и делала ей предложение в первом раунде, Барбара сумела остаться в списке больницы Гопкинса после того, как в первом раунде ее распределили в Йель; в то же время Элис была исключена из списка больницы Гопкинса. Затем Барбара получила предложение от больницы Гопкинса, что позволило ей выбыть из списка Йеля. Это привело к тому, что Йель пригласил Элис, и в Стэнфорде освободилось место для Барбары. Определение выгодного искажения предпочтений явно было непростым делом, поскольку для этого требовалось знать рейтинги как больниц, так и остальных студентов, а также алгоритм распределения, однако оно было произведено.

И действительно, студенты-медики затрачивают немало времени и сил, пытаясь узнать, что требуется различным больницам, что было характерно для их рейтинговых списков в прошлом и что, скорее всего, будут предпринимать их коллеги-студенты; они надеются, что с помощью этой информации сумеют придумать выгодные для себя ложные описания своих предпочтений. Однако, как позволяет предположить приведенный выше пример, расчет правильной стратегической дезинформации – дело тонкое и непростое. Вполне возможно, что в конце концов студенты отказываются от попыток переиграть систему и представляют точные описания своих предпочтений.

Принятая в данной главе логика позволяет предположить, что долговечности НПРИ в решающей степени способствовали ее эффективность и стабильность; аналогичным образом несостоятельность предыдущих систем можно объяснить их неэффективностью и нестабильностью.

Когда формируемое распределение неэффективно, все в общем заинтересованы в замене этого распределения другим, которое улучшит положение каждой стороны. Когда системы не являются стабильными – в том смысле, в каком этот термин интерпретируется здесь, – они отличаются особенной хрупкостью, поскольку пары агентов обладают и стимулами, и возможностями для того, чтобы исказить работу этих систем, и можно предположить, что они так и поступят.

Эти доводы могут быть подкреплены примером анализа механизмов, использовавшихся для решения проблемы распределения врачей по больницам в Великобритании. Ситуация там носит более сложный по сравнению с США характер, поскольку в Великобритании существуют семь региональных рынков, каждый из которых после периода неопределенности, схожей с той, что существовала в США до 1951 г., опробовал свои собственные алгоритмы распределения. Восемь из этих различных алгоритмов были подвергнуты формализованному анализу; два алгоритма были признаны стабильными, шесть остальных – нестабильными. Два стабильных алгоритма используются до сих пор, в то время как из шести нестабильных четыре были впоследствии отвергнуты.